NoisyPrint
最近在学习的过程中,突然想起一个在Adobe Audition中用过的功能。
为什么会想到这个功能呢,因为在我使用DeepFilter的过程中,我发现对于一些低信噪比的信号来说,DeepFilter很容易出现过拟合现象,导致音源的过度失真。那么有没有什么好办法解决这个问题呢?答案当然是有的,就是这个采样部分噪音,然后在频域上进行相减的方法。
项目地址,持续更新欢迎Star Github : LeventureQys/NoisyPrint
原理
1. 加性噪声模型
在信号处理领域,含噪声的信号通常可以被建模为:
x ( t ) = s ( t ) + n ( t ) x(t) = s(t) + n(t) x(t)=s(t)+n(t)
- x(t):观测到的含噪声信号
- s(t):原始干净信号
- n(t):噪声信号
这个模型假设噪声是加性的,并且与原始信号不相关。
2. 频域中的表示
通过短时傅里叶变换(STFT),将时域信号转换到频域:
X ( ω ) = S ( ω ) + N ( ω ) X(\omega) = S(\omega) + N(\omega) X(ω)=S(ω)+N(ω)
- X ( ω ) X(\omega) X(ω):含噪声信号的频谱
- S ( ω ) S(\omega) S(ω): 原始信号的频谱
- N ( ω ) N(\omega) N(ω): 噪声信号的频谱
这意味着在频域中,信号的频谱是线性叠加的。
综上
我们可以直接反过来计算,得到我们的 S ( ω ) S(\omega) S(ω) 然后在进行反傅里叶变换,获得时域信息。
总结流程:
- 1.采集噪声样本并建立噪声频谱模型
- 2.将含噪声的音频信号分帧处理
- 3.对每一帧进行窗函数处理
- 4.对窗化后的帧进行快速傅里叶变换(FFT)
- 5.从信号的频谱中减去噪声频谱
- 6.处理频谱减法后的负值和伪影
- 7.进行逆快速傅里叶变换(IFFT)重建时域信号
- 8.通过重叠相加(Overlap-Add)方法重建完整的信号
- 9.后处理,如频谱平滑
实操:
1.采集噪声样本并建立噪声频谱模型
这一段我直接使用Audition进行的,具体不表,总之是两段音频,分别是全音频和纯噪音
原始音频:
纯噪音:
可以看得到,这音频中明显是有比较强烈的噪音的。
2. 3. 4.
这部分暂且不表,详情见下方代码:
import numpy as np
import scipy.io.wavfile as wav
import matplotlib.pyplot as plt
from scipy.signal import get_window
from scipy.fftpack import fft, ifft
# 1. 读取纯噪声信号,建立噪声频谱模型
noise_rate, noise_data = wav.read('./AudioSource/Noisy.wav')
# 如果噪声是立体声,转换为单声道
if len(noise_data.shape) > 1:
noise_data = noise_data.mean(axis=1)
# 计算噪声频谱模型
frame_size = 1024
overlap = 512
noise_frames = []
for i in range(0, len(noise_data) - frame_size, overlap):
frame = noise_data[i:i+frame_size]
windowed_frame = frame * get_window('hamming', frame_size)
spectrum = fft(windowed_frame)
noise_frames.append(np.abs(spectrum))
# 计算平均噪声频谱
noise_spectrum = np.mean(noise_frames, axis=0)
# 2. 读取需要降噪的音频信号
rate, data = wav.read('./AudioSource/Source.wav')
if len(data.shape) > 1:
data = data.mean(axis=1)
# 保存降噪前的频谱,用于后续对比
original_spectrum = []
# 进行降噪处理
output_data = np.zeros(len(data))
window = get_window('hamming', frame_size)
for i in range(0, len(data) - frame_size, overlap):
# 2. 分帧
frame = data[i:i+frame_size]
# 3. 窗函数处理
windowed_frame = frame * window
# 4. FFT
spectrum = fft(windowed_frame)
# 保存原始频谱
original_spectrum.append(np.abs(spectrum))
# 5. 频谱减法
magnitude = np.abs(spectrum)
phase = np.angle(spectrum)
subtracted_magnitude = magnitude - noise_spectrum
# 6. 处理负值和伪影
subtracted_magnitude = np.maximum(subtracted_magnitude, 0.0)
# 7. IFFT
reconstructed_spectrum = subtracted_magnitude * np.exp(1j * phase)
reconstructed_frame = np.real(ifft(reconstructed_spectrum))
# 8. Overlap-Add 重建信号
output_data[i:i+frame_size] += reconstructed_frame * window
# 保存降噪后的频谱,用于对比
denoised_spectrum = []
for i in range(0, len(output_data) - frame_size, overlap):
frame = output_data[i:i+frame_size]
windowed_frame = frame * window
spectrum = fft(windowed_frame)
denoised_spectrum.append(np.abs(spectrum))
# 9. 后处理(可选,这里暂不实现)
# 保存降噪后的音频
wav.write('./AudioSource/Denosed.wav', rate, output_data.astype(np.int16))
# 绘制频谱对比
# 计算平均频谱
original_spectrum_mean = np.mean(original_spectrum, axis=0)
denoised_spectrum_mean = np.mean(denoised_spectrum, axis=0)
freqs = np.linspace(0, rate, frame_size)
plt.figure(figsize=(12,6))
plt.plot(freqs[:frame_size//2], 20*np.log10(original_spectrum_mean[:frame_size//2]), label='Original')
plt.plot(freqs[:frame_size//2], 20*np.log10(denoised_spectrum_mean[:frame_size//2]), label='Processed')
plt.xlabel('频率 (Hz)')
plt.ylabel('幅度 (dB)')
plt.title('降噪前后频谱对比')
plt.legend()
plt.show()
测试效果
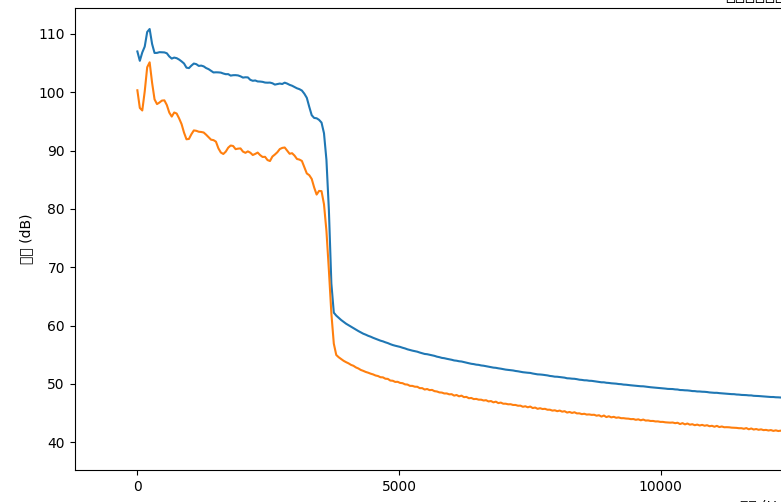
这个库还有很多可以优化的空间,可以参考Audition下的控制面板,可以简单窥见可以优化的空间:
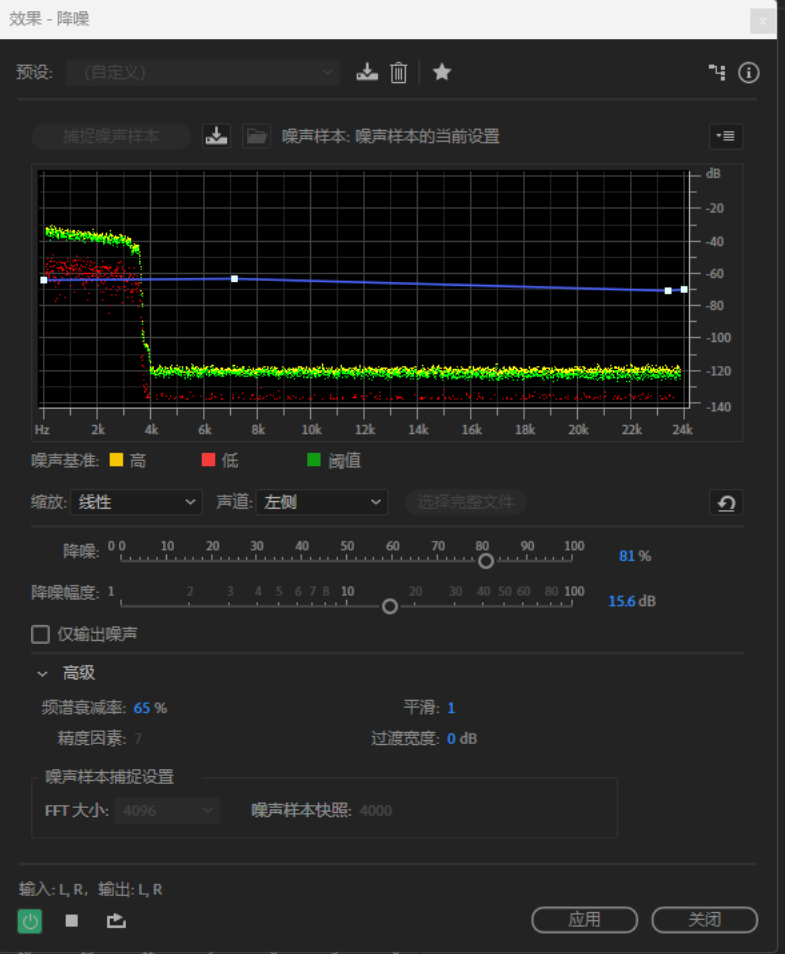
-
1.优化曲线频域相减对于频域下不同值的曲线增益因子 r \mathcal{r} r在这里是没有考虑的,在实际的使用中是可以进行考虑的。
-
2.这里是直接简单粗暴的直接减掉了所有的频域内容,实际上可以不那么生硬地进行剪辑。
-
3.可以使用小范围的 FFT来进行实时性音频降噪的尝试。
-
4.进行C++的移植,实际上这些库都有。