零 相关资料
官方网址
官方网址下的API搜索网站
一 定义
深度学习框架是用于设计、训练和部署深度学习模型的软件工具包。这些框架提供了一系列预定义的组件,如神经网络层(卷积层、全连接层等)、损失函数、优化器以及数据处理工具,使得开发者可以更加高效地构建复杂的机器学习模型。此外,它们还通常包含自动微分功能,这极大地简化了梯度计算过程,这是训练神经网络时反向传播算法的核心部分。
一些流行的深度学习框架包括:
TensorFlow - 由Google开发,支持多种语言接口,如Python、C++等,并且拥有一个活跃的社区和丰富的资源库。TensorFlow提供了Keras作为其高级API,方便用户快速搭建模型。
PyTorch - 由Facebook的人工智能研究实验室(FAIR)开发,以动态计算图著称,特别适合于需要灵活实验的研究者。它也使用Python作为主要编程语言,并且因其直观易用而受到广泛欢迎。
二 基础知识
1. .cuda()作用
将计算由CPU转移至GPU;
可以将变量转移,也可以对函数转移
import torch
# 创建一个张量
x = torch.tensor([1.0, 2.0, 3.0])
# 将张量移动到 GPU
x = x.cuda()
# 或者对于模型
model = MyModel()
model = model.cuda()
如果机器上有多个 GPU,可以在 .cuda() 中指定 GPU 的索引,例如 x.cuda(0) 将张量移动到第一个 GPU。
2 tensor打印属性介绍
# requires_grad,grad_fn,grad的含义及使用
requires_grad: 如果需要为张量计算梯度,则为True,否则为False。我们使用pytorch创建tensor时,可以指定requires_grad为True(默认为False),
grad_fn: grad_fn用来记录变量是怎么来的,方便计算梯度,y = x*3,grad_fn记录了y由x计算的过程。
grad:当执行完了backward()之后,通过x.grad查看x的梯度值。
创建一个Tensor并设置requires_grad=True,requires_grad=True说明该变量需要计算梯度。
>>x = torch.ones(2, 2, requires_grad=True)
tensor([[1., 1.], [1., 1.]], requires_grad=True)
>>print(x.grad_fn) # None
3 张量
玩转Pytorch张量(Tensor)
一、什么是张量(Tensor)?
Tensor是Pytorch中最底层的核心的数据结构。Pytorch中的所有操作都是在张量的基础上进行的。

也就是说,一个Tensor是一个包含单一数据类型的多维矩阵。通常,其多维特性用三维及以上的矩阵来描述,例如下图所示:单个元素为标量(scalar),一个序列为向量(vector),多个序列组成的平面为矩阵(matrix),多个平面组成的立方体为张量(tensor)。
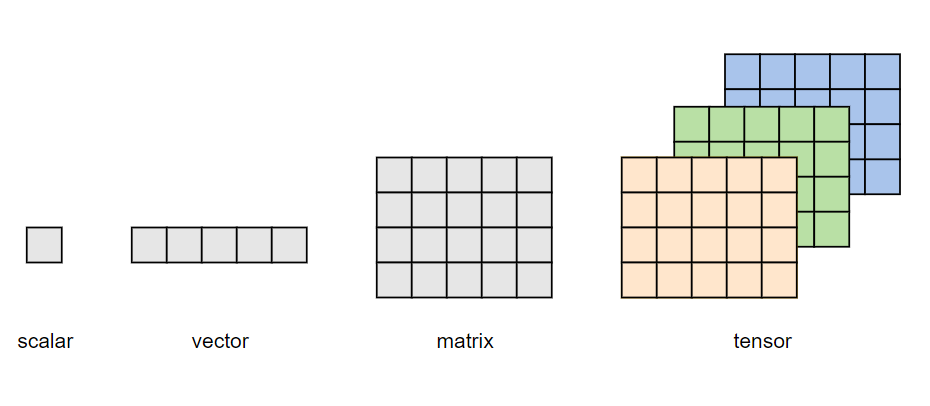
当然,张量也无需严格限制在三维及以上才叫张量,就像矩阵也有一维、二维矩阵乃至多维矩阵之分一样。
「在深度学习的范畴内,标量、向量和矩阵也可分为称为零维张量、一维张量、二维张量。」
二、为什么深度学习要搞出Tensor?
熟悉机器学习的小伙伴们应该都知道,有监督机器学习模型的输入X通常是多个特征列组成的二维矩阵,输出y是单个特征列组成的标签向量或多个特征列组成的二维矩阵。那么深度学习中,为何要定义多维矩阵Tensor呢?
深度学习当前最成熟的两大应用方向莫过于CV和NLP,其中CV面向图像和视频,NLP面向语音和文本,二者分别以卷积神经网络和循环神经网络作为核心基础模块,且标准输入数据集都是至少三维以上。其中,
- 图像数据集:至少包含三个维度(样本数Nx图像高度Hx图像宽度W);如果是彩色图像,则还需增加一个通道C,包含四个维度(NxHxWxC);如果是视频帧,可能还需要增加一个维度T,表示将视频划分为T个等时长的片段。
- 文本数据集:包含三个维度(样本数N×序列长度L×特征数H)。
因此,输入学习模型的输入数据结构通常都要三维以上,这也就促使了Tensor的诞生。
三、Tensor创建
1.使用torch.tensor()函数直接创建
在PyTorch中,torch.tensor()函数用于直接从Python的数据结构(如列表、元组或NumPy数组)中创建一个新的张量。
"""
data:数据,可以是list,numpy
dtype:数据类型,默认与data对应
device:张量所在的设备(cuda或cpu)
requires_grad:是否需要梯度
pin_memory:是否存于锁存内存
"""
torch.tensor(data,dtype=None,device=None,requires_grad=False,pin_memory=False)
pin_memor用于实现锁页内存,创建DataLoader时,设置pin_memory=True,则意味着生成的Tensor数据最开始是属于内存中的锁页内存,这样将内存的Tensor转义到GPU的显存就会更快一些。
如需创建一个放在GPU的数据,则可做如下修改,运行结果同上。
import numpy as np
import torch
device= torch.device("cuda" if torch.cuda.is_available() else 'cpu')
arr = np.ones((3, 3))
print("ndarray的数据类型:", arr.dtype)
t = torch.tensor(arr, device=device)
print(t)
2.根据数值创建张量
'''
size:张量的形状
out:输出的张量,如果指定了out,torch.zeros()返回的张量则会和out共享同一个内存地址
layout:内存中的布局方式,有strided,sparse_coo等。如果是稀疏矩阵,则可以设置为sparse_coo以减少内存占用
device:张量所在的设备(cuda或cpu)
requires_grad:是否需要梯度
'''
torch.zeros(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)
四、Tensor属性
1.Tensor形状
张量具有如下形状属性:
- Tensor.ndim:张量的维度,例如向量的维度为1,矩阵的维度为2。
- Tensor.shape:张量每个维度上元素的数量。
- Tensor.shape[n]:张量第n维的大小。第n维也称为轴(axis)。
- Tensor.numel:张量中全部元素的个数。
import torch
Tensor=torch.ones([2,3,4,5])
print("Number of dimensions:", Tensor.ndim)
print("Shape of Tensor:", Tensor.shape)
print("Elements number along axis 0 of Tensor:", Tensor.shape[0])
print("Elements number along the last axis of Tensor:", Tensor.shape[-1])
print('Number of elements in Tensor: ', Tensor.numel()) #用.numel表示元素个数
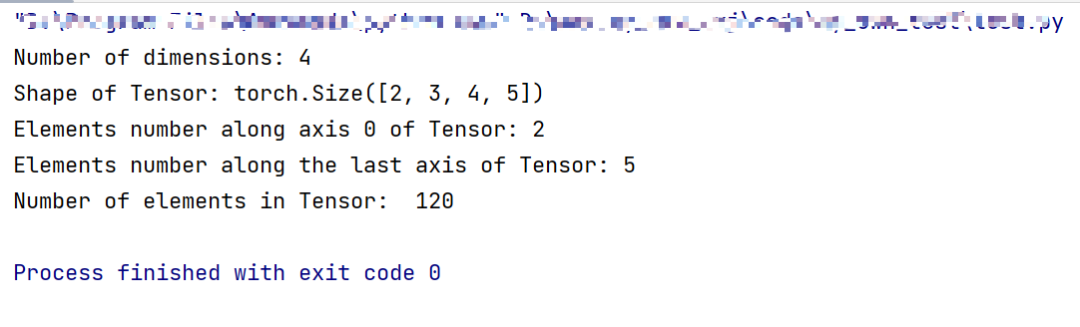
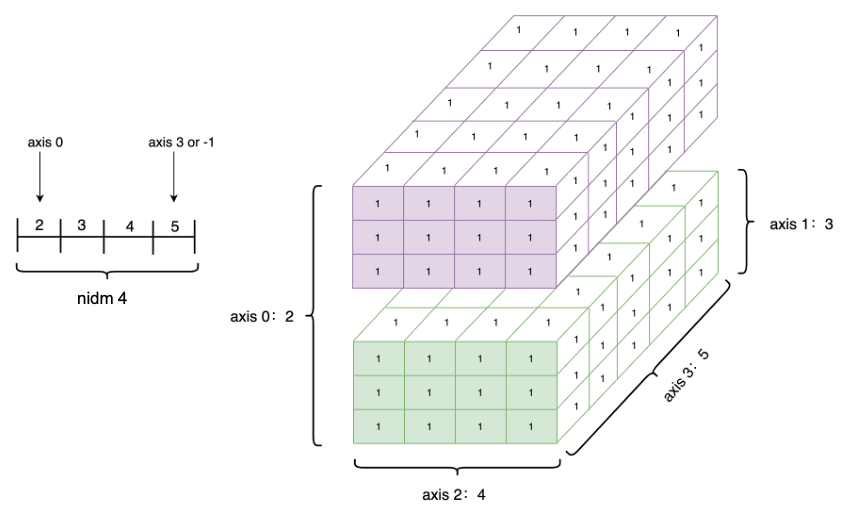
如下是创建一个四维Tensor,并通过图形直观表达以上几个概念的关系。
Tensor的axis、shape、dimension、ndim之间的关系如下图所示。
五、Tensor操作
1.形状重置
Tensor的shape可通过torch.reshape接口来改变。例如:
import torch
Tensor =torch.tensor([[[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]],
[[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30]]])
print("the shape of Tensor:", Tensor.shape)
#利用reshape改变形状
reshape_Tensor = torch.reshape(Tensor, [2, 5, 3])
print("After reshape:\n", reshape_Tensor)

从输出结果看,将张量从[3, 2, 5]的形状reshape为[2, 5, 3]的形状时,张量内的数据不会发生改变,元素顺序也没有发生改变,只有数据形状发生了改变。
在指定新的shape时存在一些技巧:
-1 表示这个维度的值是从Tensor的元素总数和剩余维度自动推断出来的。因此,有且只有一个维度可以被设置为-1。
0 表示该维度的元素数量与原值相同,因此shape中0的索引值必须小于Tensor的维度(索引值从 0 开始计,如第 1 维的索引值是 0,第二维的索引值是 1)。
# 直接指定目标 shape
origin:[3, 2, 5] reshape:[3, 10] actual: [3, 10]
# 转换为 1 维,维度根据元素总数推断出来是 3*2*5=30
origin:[3, 2, 5] reshape:[-1] actual: [30]
# 转换为 2 维,固定一个维度 5,另一个维度根据元素总数推断出来是 30÷5=6
origin:[3, 2, 5] reshape:[-1, 5] actual: [6, 5]
# reshape:[0, -1]中 0 的索引值为 0,按照规则
# 转换后第 0 维的元素数量与原始 Tensor 第 0 维的元素数量相同,为3
# 第 1 维的元素数量根据元素总值计算得出为 30÷3=10。
origin:[3, 2, 5] reshape:[0, -1] actual: [3, 10]
# reshape:[3, 1, 0]中 0 的索引值为 2
# 但原 Tensor 只有 2 维,无法找到与第 3 维对应的元素数量,因此出错。
origin:[3, 2] reshape:[3, 1, 0] error:
4 nn.Embedding
详见nn.Embedding解析
nn.Embedding 是它的主要作用是将输入的整数序列映射为连续的向量表示
nn.Embedding 的输入通常是一个整数索引(代表词汇或符号),输出是对应的向量表示。该模块可以看作是一个查找表,其中每个词汇都有一个与之对应的向量。具体来说,它有两个关键参数:
num_embeddings: 词汇表的大小,即可以嵌入的词汇数量。embedding_dim: 每个词汇对应的向量维度。
注:embeddings中的值是正态分布N(0,1)中随机取值。
如何使用
在NLP任务中,首先要对文本进行处理,将文本进行编码转换,形成向量表达,embedding处理文本的流程如下:
(1)输入一段文本,中文会先分词(如jieba分词),英文会按照空格提取词
(2)首先将单词转成字典的形式,由于英语中以空格为词的分割,所以可以直接建立词典索引结构。类似于:word2id = {‘i’ : 1, ‘like’ : 2, ‘you’ : 3, ‘want’ : 4, ‘an’ : 5, ‘apple’ : 6} 这样的形式。如果是中文的话,首先进行分词操作。
(3)然后再以句子为list,为每个句子建立索引结构,list [ [ sentence1 ] , [ sentence2 ] ] 。以上面字典的索引来说,最终建立的就是 [ [ 1 , 2 , 3 ] , [ 1 , 4 , 5 , 6 ] ] 。这样长短不一的句子
(4)接下来要进行padding的操作。由于tensor结构中都是等长的,所以要对上面那样的句子做padding操作后再利用 nn.Embedding 来进行词的初始化。padding后的可能是这样的结构
[ [ 1 , 2 , 3, 0 ] , [ 1 , 4 , 5 , 6 ] ] 。其中0作为填充。(注意:由于在NMT任务中肯定存在着填充问题,所以在embedding时一定存在着第三个参数,让某些索引下的值为0,代表无实际意义的填充)
比如有两个句子:
I want a plane
I want to travel to Beijing
将两个句子转化为ID映射:
{I:1,want:2,a:3,plane:4,to:5,travel:6,Beijing:7}
转化成ID表示的两个句子如下:
1,2,3,4
1,2,5,6,5,7
import torch
from torch import nn
# 创建最大词个数为10,每个词用维度为4表示
embedding = nn.Embedding(10, 4)
# 将第一个句子填充0,与第二个句子长度对齐
in_vector = torch.LongTensor([[1, 2, 3, 4, 0, 0], [1, 2, 5, 6, 5, 7]])
out_emb = embedding(in_vector)
print(in_vector.shape)
print((out_emb.shape))
print(out_emb)
print(embedding.weight)
torch.Size([2, 6]) # 2行6列
torch.Size([2, 6, 4]) #2个6行4列
tensor([[[-0.6642, -0.6263, 1.2333, -0.6055],
[ 0.9950, -0.2912, 1.0008, 0.1202],
[ 1.2501, 0.1923, 0.5791, -1.4586],
[-0.6935, 2.1906, 1.0595, 0.2089],
[ 0.7359, -0.1194, -0.2195, 0.9161],
[ 0.7359, -0.1194, -0.2195, 0.9161]],
[[-0.6642, -0.6263, 1.2333, -0.6055],
[ 0.9950, -0.2912, 1.0008, 0.1202],
[-0.3216, 1.2407, 0.2542, 0.8630],
[ 0.6886, -0.6119, 1.5270, 0.1228],
[-0.3216, 1.2407, 0.2542, 0.8630],
[ 0.0048, 1.8500, 1.4381, 0.3675]]], grad_fn=<EmbeddingBackward0>)
Parameter containing:
tensor([[ 0.7359, -0.1194, -0.2195, 0.9161],
[-0.6642, -0.6263, 1.2333, -0.6055],
[ 0.9950, -0.2912, 1.0008, 0.1202],
[ 1.2501, 0.1923, 0.5791, -1.4586],
[-0.6935, 2.1906, 1.0595, 0.2089],
[-0.3216, 1.2407, 0.2542, 0.8630],
[ 0.6886, -0.6119, 1.5270, 0.1228],
[ 0.0048, 1.8500, 1.4381, 0.3675],
[ 0.3810, -0.7594, -0.1821, 0.5859],
[-1.4029, 1.2243, 0.0374, -1.0549]], requires_grad=True)
例如,如果你有一个大小为 1000 的词汇表,并希望每个词汇用一个 300 维的向量来表示,你可以这样定义 nn.Embedding:
import torch.nn as nn
# 词汇表大小为 1000,每个词汇的嵌入维度为 300
embedding = nn.Embedding(num_embeddings=1000, embedding_dim=300)
# 输入一个词汇索引
input = torch.tensor([1, 2, 3, 4])
# 获取对应的嵌入向量
output = embedding(input)
print("output_size:",output.size(),"\n.output:",output)
------------------------------------
output_size: torch.Size([4, 300])
.output: tensor([[ 2.3543, 1.1523, -1.6173, ..., -0.5308, -0.8865, 0.1191],
[ 0.9140, 0.1824, -0.6363, ..., 0.9007, -0.3558, 2.0714],
[ 1.0525, 0.0092, 0.8510, ..., 0.7767, -1.3282, 0.1715],
[ 0.8045, 1.3735, 0.7389, ..., -1.2809, -0.4609, 0.4125]],
grad_fn=<EmbeddingBackward0>)
参考
https://pytorch.org/docs/stable/generated/torch.nn.Embedding.html
3 nn.Dropout用法与作用
nn.Dropout 是 PyTorch 中的一个模块,用于防止神经网络过拟合的一种正则化技术。它的主要作用是在训练期间随机将一部分神经元的输出设为零(即“丢弃”),从而减少模型对特定神经元的依赖,增强模型的泛化能力。
用法
在使用 nn.Dropout 时,你可以指定一个 p 参数,该参数表示在每次前向传播时,以多大的概率将神经元的输出置零。p 的取值范围在 0 到 1 之间,通常设为 0.5 左右。
import torch
import torch.nn as nn
# 创建一个 Dropout 层,丢弃率为 0.5
dropout = nn.Dropout(p=0.5)
# 输入数据
input_data = torch.randn(5, 10)
# 应用 Dropout 层
output_data = dropout(input_data)
print("input_size:",input_data.size(),"\n.input:",input_data)
print("output_size:",output_data.size(),"\n.output:",output_data)
-----------------------------
input_size: torch.Size([5, 10])
.input: tensor([[ 0.4757, 1.0549, 0.4897, -0.3439, 0.9176, 0.2441, 0.4073, 0.0852,
-0.3969, -0.7151],
[-0.4394, 0.7188, 0.7403, -0.1388, 0.9963, 0.0678, 1.1171, 0.4086,
-0.1567, -0.4750],
[-0.0219, -0.2155, -0.2252, -0.7611, 1.4713, -0.5379, 0.4363, -1.5307,
-0.9243, -0.5168],
[-0.3247, 0.9712, -0.4859, 0.2869, -0.9935, -0.8477, 2.1244, -0.0360,
0.3316, -1.1796],
[-2.4401, -0.3394, -0.4239, -0.1039, -1.7476, 0.5174, -1.0108, -0.2301,
-0.1675, -0.1827]])
output_size: torch.Size([5, 10])
.output: tensor([[ 0.0000, 0.0000, 0.0000, -0.0000, 0.0000, 0.4881, 0.0000, 0.1704,
-0.7937, -0.0000],
[-0.8789, 0.0000, 0.0000, -0.0000, 1.9926, 0.0000, 0.0000, 0.8172,
-0.3134, -0.0000],
[-0.0439, -0.0000, -0.4504, -0.0000, 0.0000, -0.0000, 0.8727, -3.0614,
-1.8487, -0.0000],
[-0.6495, 1.9424, -0.9717, 0.5739, -0.0000, -1.6955, 4.2488, -0.0000,
0.0000, -0.0000],
[-4.8802, -0.6788, -0.0000, -0.0000, -0.0000, 1.0348, -0.0000, -0.0000,
-0.3349, -0.3654]])
另外还可以通过如下方式改变shape:
torch.squeeze:可实现Tensor的降维操作,即把Tensor中尺寸为1的维度删除。
torch.unsqueeze:可实现Tensor的升维操作,即向Tensor中某个位置插入尺寸为1的维度。
torch.flatten,将Tensor的数据在指定的连续维度上展平。
torch.transpose,对Tensor的数据进行重排。
4 维度变换
1. pe
pe 是一个二维张量,表示位置编码矩阵。它的形状是 [max_len, d_model],其中 max_len 是序列的最大长度,d_model 是每个位置的嵌入维度。每一行对应一个位置的编码。
2. pe.unsqueeze(0)
unsqueeze 函数会在指定位置添加一个新的维度。在这里,pe.unsqueeze(0) 会在第 0 维添加一个新的维度,使 pe 的形状从 [max_len, d_model] 变成 [1, max_len, d_model]。添加这个新维度是为了方便后续的批处理操作,这个维度通常表示批次(batch)。
3. pe.transpose(0, 1)
transpose 函数用于交换张量的两个维度。在这里,pe.transpose(0, 1) 将第 0 维和第 1 维交换,即将形状从 [1, max_len, d_model] 变成 [max_len, 1, d_model]。这样操作的目的是将位置维度放到第一维,这样可以很方便地对序列中的每个位置进行操作。
总结
经过这两个操作后,位置编码张量 pe 的形状变为 [max_len, 1, d_model]。这样做的目的是为了在前向传播时能够将位置编码添加到输入序列的每个位置上。具体来说,当有一个输入张量 x,其形状为 [seq_len, batch_size, d_model] 时,通过 x = x + self.pe[:x.size(0), :] 将位置编码加到 x 上。由于 self.pe[:x.size(0), :] 的形状为 [seq_len, 1, d_model],它可以自动广播(broadcast)以匹配 x 的形状。
参考
- # Transformer 的 Pytorch 代码实现讲解
- # Pytorch中nn.Module和nn.Sequencial的简单学习
三 类相关
1 多继承
类的继承与重载
# Pytorch构建网络模型时super(class, self).init()的作用
# Python多继承与super使用详解
# python多继承及其super的用法