摘要
路径规划是机器人导航和自主无人机领域中的关键问题。本文提出了一种基于智能优化算法——樽海鞘群算法(Salp Swarm Algorithm, SSA)的二维路径规划方法。该算法模拟樽海鞘的链式运动行为,旨在寻找障碍物环境中的最优路径。通过仿真实验验证,SSA算法能够快速收敛并找到路径长度最短的安全路径。
理论
-
问题描述:二维路径规划问题通常可以表述为在二维平面中,从起点到目标点找到一条避开障碍物的路径。目标是使得路径的代价最小(通常是距离),同时避免与障碍物发生碰撞。
-
樽海鞘群算法(SSA)原理:
-
樽海鞘群算法是一种基于群体智能的优化算法,它模仿樽海鞘在水中的链式移动行为。樽海鞘群中的个体分为领导者和追随者,领导者负责探索新的搜索空间,追随者根据链式结构跟随领导者。
-
领导者的位置更新公式为:
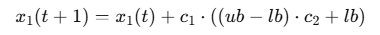
其中, 𝑐1和𝑐2 是随机数,𝑢𝑏和𝑙𝑏分别表示搜索空间的上界和下界。
-
追随者的位置更新公式为:
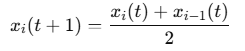
这种位置更新机制使得群体能够在较短时间内找到最优解。
实验结果
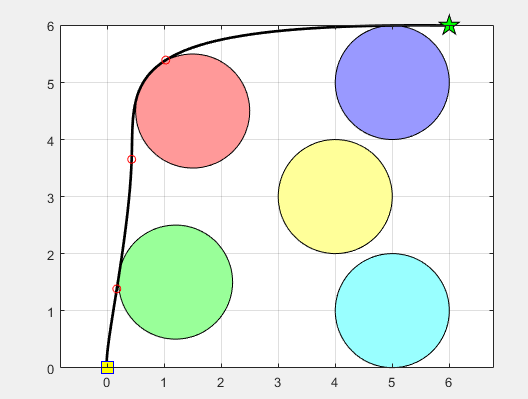
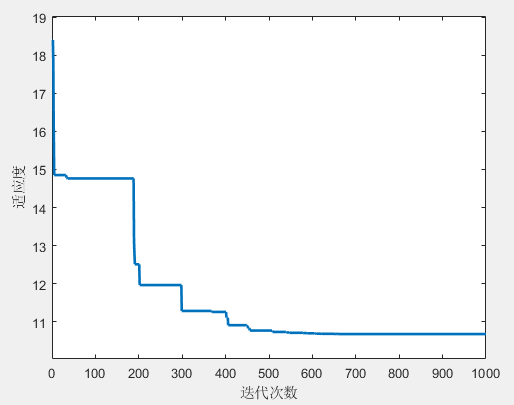
如图所示(图1),实验显示樽海鞘群算法能够成功规划出一条避开障碍物的路径(从左下角起点到右上角目标点)。黑色曲线代表规划出的路径,红色圆圈代表关键路径点,黄色和绿色方框分别表示起点和目标点,五个彩色圆形为障碍物。图2显示了适应度函数值(路径长度)的收敛曲线,经过约 1000 代的迭代后,适应度值趋于稳定,表明算法已找到较优的路径。
部分代码
以下为部分SSA算法在路径规划中的实现代码:
% 樽海鞘群算法(SSA)的实现
function SSA_path_planning()
% 初始化参数
max_iter = 1000; % 最大迭代次数
pop_size = 50; % 种群大小
dim = 2; % 问题维度(二维)
% 初始化位置
lb = [0, 0]; % 搜索空间下界
ub = [6, 6]; % 搜索空间上界
population = lb + (ub - lb).*rand(pop_size, dim); % 随机初始化
for iter = 1:max_iter
% 更新位置
for i = 1:pop_size
% 领导者更新
if i == 1
population(i, :) = leader_update(population(i, :), lb, ub);
else
% 追随者更新
population(i, :) = (population(i, :) + population(i-1, :)) / 2;
end
end
% 计算适应度
fitness = calculate_fitness(population);
end
end
参考文献
❝
Mirjalili, S., & Lewis, A. (2016). The Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Advances in Engineering Software, 114, 163-191.
Yang, X. S., & Deb, S. (2009). Cuckoo search via Lévy flights. Proceedings of the World Congress on Nature & Biologically Inspired Computing, 210-214.
Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. Proceedings of IEEE International Conference on Neural Networks, 1942-1948.