1、含有n个非叶结点的m阶B树中至少包含()个关键字。
- A:n(m+1)
- B:n
- C:n( ┌ \ulcorner ┌m/2 ┐ \urcorner ┐-1)
- D:(n-1)( ┌ \ulcorner ┌m/2 ┐ \urcorner ┐-1)+1
解析
除根结点外,m阶B树中的每个非叶结点至少有 ┌ \ulcorner ┌m/2 ┐ \urcorner ┐-1个关键字,根结点至少有一个关键字,所以总共包含的关键字最少个数=(n-1)( ┌ \ulcorner ┌m/2 ┐ \urcorner ┐-1)+1。
答案:D
2、已知一棵5阶B树中共有53个关键字,则树的最大高度为(),最小高度为()。
- A:2
- B:3
- C:4
- D:5
解析
5阶B树中共有53个关键字,由最大高度公式H ≤ \leq ≤ log ┌ m / 2 ┐ \log_{\ulcorner{m/2}\urcorner} log┌m/2┐((n+1)/2)+1得最大高度H ≤ \leq ≤ log 3 \log_3 log3[(53+1)/2]+1=4,即最大高度为4;由最小高度公式h ≥ \geq ≥ log m \log_m logm(n+1)得最小高度h ≥ \geq ≥$\log_5$54=2.5,从而最小高度为3。
答案:C。B
3、已知一棵3阶B树中有2047个关键字,则此B树的最大高度为(),最小高度为()。
- A:11
- B:10
- C:8
- D:7
解析
利用最小高度h ≥ \geq ≥ log m \log_m logm(n+1)和最大高度H ≤ \leq ≤ log ┌ m / 2 ┐ \log_{\ulcorner{m/2}\urcorner} log┌m/2┐((n+1)/2)+1的公式。可以算出最大高度H ≤ \leq ≤ log 2 \log_2 log2[(2047+1)/2]+1=11,最小高度h ≥ \geq ≥ log 3 \log_3 log3 2048=6.9,从而最小高度取7。
答案:A。D
4、下列关于B树和B+树的叙述中,不正确的是()。
- A:B树和B+树都能有效地支持顺序查找
- B:B树和B+树都能有效地支持随机查找
- C:B树和B+树都是平衡的多叉树
- D:B树和B+树都可以用于文件索引结构
解析
B树和B+树的差异主要体现在:1.结点关键字和子树的个数;2.B+树非叶结点仅起索引作用;3.B树叶结点关键字和其他结点包含的关键字是不重复的;4.B+树支持顺序查找和随机查找。而B树仅支持随机查找。
由于B+树的所有叶结点中包含了全部的关键字信息,且叶结点本身依关键字从小到大顺序链接,因此可以进行顺序查找,而B树不支持顺序查找。
答案:A
5、在一棵高度为2的5阶B树中,所含关键字的个数至少是()。
- A:5
- B:7
- C:8
- D:14
解析
答案:A
6、在一棵有15个关键字的4阶B树中,含关键字的结点的个数最多是()。
- A:5
- B:6
- C:10
- D:15
解析
关键字数量不变,要求结点数量最多,即要求每个结点中含关键字的数量最少。根据4阶B树的定义,根结点最少含1个关键字,非根结点中最少含 ┌ 4 / 2 ┐ \ulcorner{4/2}\urcorner ┌4/2┐-1=1个关键字,所以每个结点中关键字数量最少都为1个,即每个结点都有2个分支,类似于排序二叉树,而15个结点正好可以构造一个4层的4阶B树,使得终端结点全在第四层,符合B树的定义,因此选D。
答案:D
7、B+树不同于B树的特点之一是()。
- A:能支持顺序查找
- B:节点中含有关键字
- C:根结点至少有两个分支
- D:所有叶结点都在同一层上
解析
由于B+树的所有叶结点中包含了全部的关键字信息,且叶结点本身依关键字从小到大顺序链接,因此可以进行顺序查找,而B树不支持顺序查找(只支持多路查找)。
答案:A
8、高度为5的3阶B树含有的关键字个数至少是()。
- A:15
- B:31
- C:62
- D:242
解析
m阶B树的基本性质:根结点以外的非叶结点最少含有 ┌ m / 2 ┐ \ulcorner{m/2}\urcorner ┌m/2┐-1个关键字,代入m=3得到每个非叶结点中最少包含1个关键字,而根结点含有1个关键字,因此所有非叶结点都有两个孩子。此时其树形与h=5的满二叉树相同,可求得关键字最少为31个。
答案:B
9、依次将关键字5,6,9,13,8,2,12,15插入初始为空的4阶B树后,根结点包含的关键字是()。
- A:8
- B:6,9
- C:8,13
- D:9,12
解析
一个4阶B树的任意非叶结点至多含有m-1=3个关键字,在关键字依次插入的过程中,会导致结点的不断分裂,插入过程如下所示。
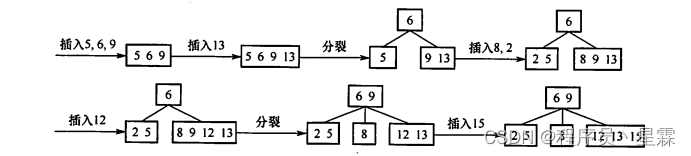
得到根结点包含的关键字为6,9。
答案:B
10、下列关于散列表的说法中,正确的是()。
Ⅰ、若散列表的填装因子
α
\alpha
α<1,则可避免碰撞的产生
Ⅱ、散列查找中不需要任何关键字的比较
Ⅲ、散列表在查找成功时平均查找长度与表长有关
Ⅳ、若在散列表中删除一个元素,不能简单地将该元素删除
- A:Ⅰ和Ⅳ
- B:Ⅱ和Ⅲ
- C:Ⅲ
- D:Ⅳ
解析
- 冲突(碰撞)是不可避免的,与装填因子无关,因此需要设计处理冲突的方法,Ⅰ错误。
- 散列查找的思想是计算出散列地址来进行查找,然后比较关键字以确定是否查找成功,Ⅱ错误。
- 散列查找成功的平均查找长度与装填因子有关,与表长无关,Ⅲ错误。
- 在开放地址的情形下,不能随便删除散列表中的某个元素,否则可能会导致搜索路径被中断(因此通常的做法是在要删除的地方做删除标记,而不是直接删除),Ⅳ正确。





![[datawhale202211]跨模态神经搜索实践:前端简介 Streamlit](https://img-blog.csdnimg.cn/616b18f61a3149b2bd541f5b00c48bfb.png)
![[python]basemap后安装后hello world代码](https://img-blog.csdnimg.cn/c5f2b969eb034153b300e1044a2ca431.png)