1.啥是队列

2.队列实现

3.Queue接口的介绍以及队列的使用

4.相关队列的例子

（1）啥是队列

我们之前讲解了栈，栈和队列是有点区别的

我们说过栈是一种先进后出的数据结构，你可以把它想象成羽毛球筒；然而队列属于一种先进先出的数据结构，队列嘛，就跟你排队做核酸排队打饭一样咯，你先排，你就先桶嗓子眼，你先排你就先打到饭（当然是不能有插队的情况啦~队列中也没有插队的概念，不会说在中间位置插入元素）

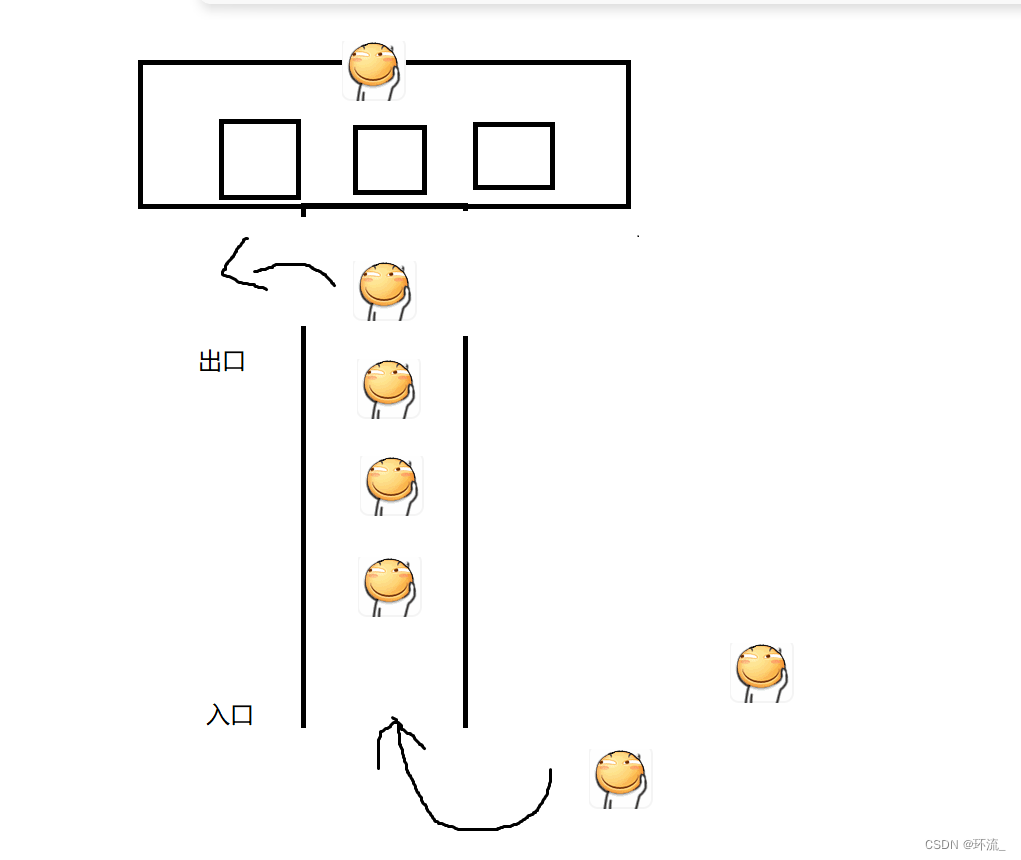
 上图就是你每次去食堂打饭的样子，元素从队尾进，从队首出~~~

---

（2）队列的实现

队列的底层是一个链表，用节点来连接，LinkedLIst实现了Queue接口，因此可以使用Linkedlist来实现一个队列

队列分为：普通队列，双端队列（Deque），优先级队列（堆）

由于堆是之后会介绍的一种数据结构，这里我们就来说说普通队列和双端队列

普通队列就是排队咯，它只有一个方向，遵循先进先出的特点，而双端队列是有两个方向的，你可以同不同的方向进，但你然需要遵循先进先出的特点，简单来说：普通队列是单行道，双端队列是双行道~

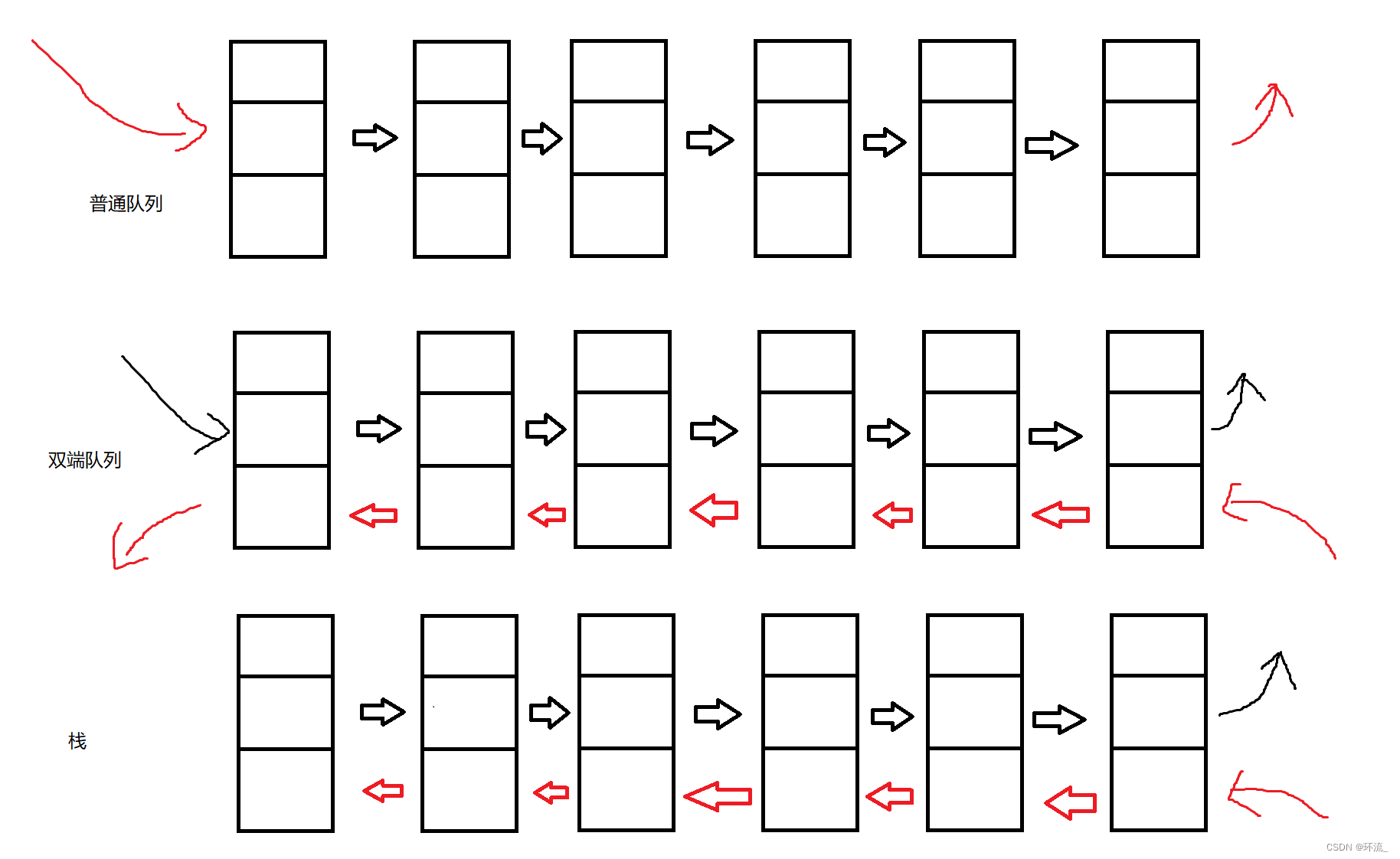
 上图展示了双链表的强大之处，使用双链表我们可以实现普通队列，实现双端队列，还可以实现栈~

当然，双链表这么牛逼，使用来实现一个队列岂不是小菜一碟~所以我们提升一下难度，我们不用双链表实现队列，我们改用单链表来实现队列！！！！！

---

我们知道单链表的形式，可以头插尾插，然后还有一个头节点head(这不是虚拟头节点，而是代表第一个元素~)

接下来我们看看怎么使用一个单链表来实现队列，这里我们理想的方式是使队列的入队和出队操作的时间复杂度都分别达到O(1)（遵循先进先出的规则）

1.头插法入队，删除尾巴节点出队（先进先出）——头插的时间复杂度是O(1)，我们有一个头节点head，因此不需要遍历，可以直接头插插入，因此我们使用头插入队；然后我们删除尾巴节点来出队，我们想要删除尾巴节点来实现出队，这样才能完成先进先出的特点，但是我们发现删除尾巴节点出队的话，需要遍历，因此出队操作的时间复杂度达到了O(N)；这貌似不是我们想要的 0_0

2.尾插法入队，删除头节点出队（先进先出）——我们使用尾插法的话，我们每次插入都要去遍历去寻找最后一个节点，导致入队操作的时间复杂度达到了O(N)，但我们删除头节点的时间复杂度却是O(1)，可是吧，我们的初衷是想入队出队都达到O(1)哦~

3.那我们还能怎么办？当然是发挥我们的主观能动性，上述两个方式结合一下啦~我们仍然需要遵循先进先出的规定，既然这样，我们仍然采用尾插法入队，但这里要给尾巴节点设置一个tail标志，用来记住尾巴节点，这样每次插入才能直接找到尾巴节点，不需要遍历，从而使入队达到O(1),而我们删除头节点来出队，头节点随时被记录着，所以删除头节点来出队，自然是O(1)~

那么下面是自定义实现普通队列的代码（有注解）

/**
 * 使用单链表加上标记尾巴节点来实现出队和入队都是O(1)的队列
 */
public class MyQueue {

    //创建节点
    static class Node{
        public int val;
        public Node next;
        public Node(int val){
            this.val = val;
        }
    }

    //创建队列的头和尾
    public Node head;
    public Node tail;

    /**
     * 入队操作
     * 当没有元素的时候
     * 当有元素的时候
     */
    public void offer(int val){
        Node node = new Node(val);
        if(head == null){
            head = node;
            tail = node;
        }else {
            tail.next = node;//使用有标记的尾插，达到O(1)
            //tail = node;
            tail = tail.next;
        }
    }

    /**
     * 出队操作
     * 判断是否有节点的情况
     * 判断是否只有一个节点的情况
     * 判断有多个节点的情况
     * 出队是要返回值的，记得保存好头节点，删除头节点后要返回
     */
    public int poll(){
        if(head == null){
            return -1;//这里也可以抛出一个异常
        }
        //要先提前记录好头节点
        int oldVal = head.val;
        if(head.next == null){
            //这是只有一个节点的情况
            //直接让head和tail指向空即可
            /*head = null;
            tail = null;*/
            head = tail = null;//可以连在一起这样写
        }else {
            //这里是有两个节点或以上的情况
            //直接让head变为当前头节点的下一个节点即可
            head = head.next;
        }
        //最后这里要返回出队的原始头节点的值
        return oldVal;
    }

    /**
     * 查看当前队头元素
     */
    public int peek(){
        if(head == null){
            return -1;//这里也可以抛出一个异常
        }
        return head.val;
    }
}

以上就是使用单链表实现一个队列的简单操作，入队出队时间复杂度均为O(1)

---

（3）介绍Queue接口以及队列的使用

 

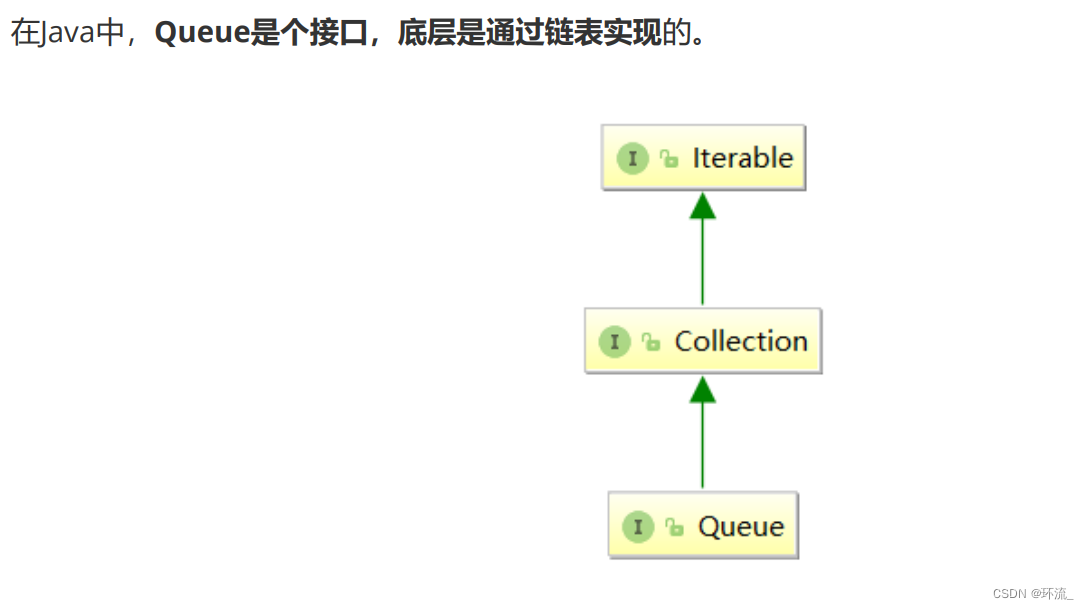
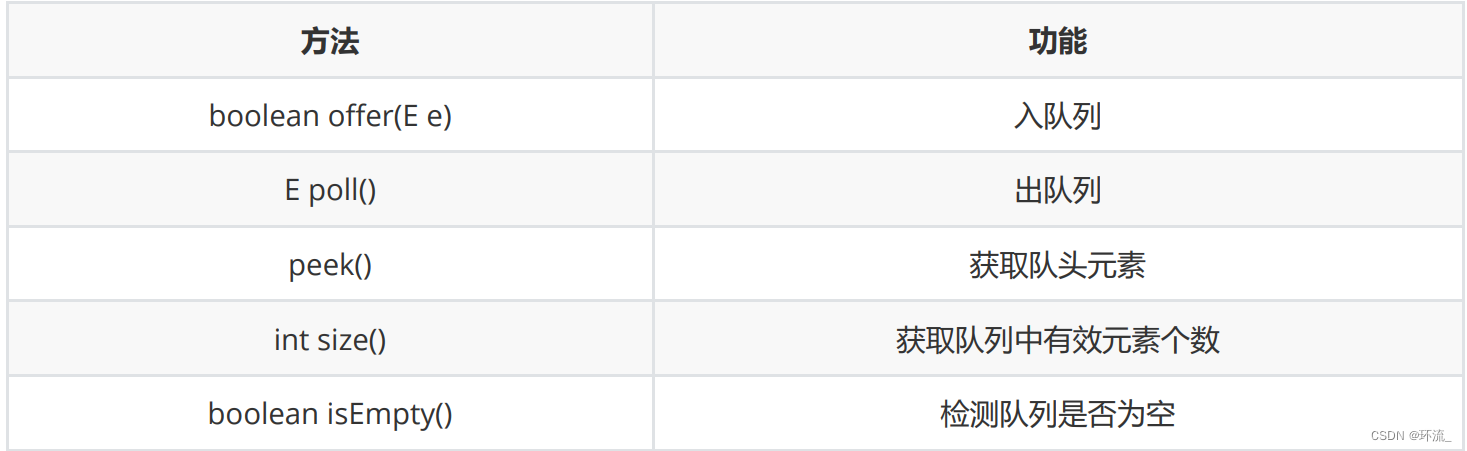
 （图片来源：比特高博）

注意：Queue是个接口，在实例化时必须实例化LinkedList的对象，因为LinkedList实现了Queue接口。

 

---

循环队列

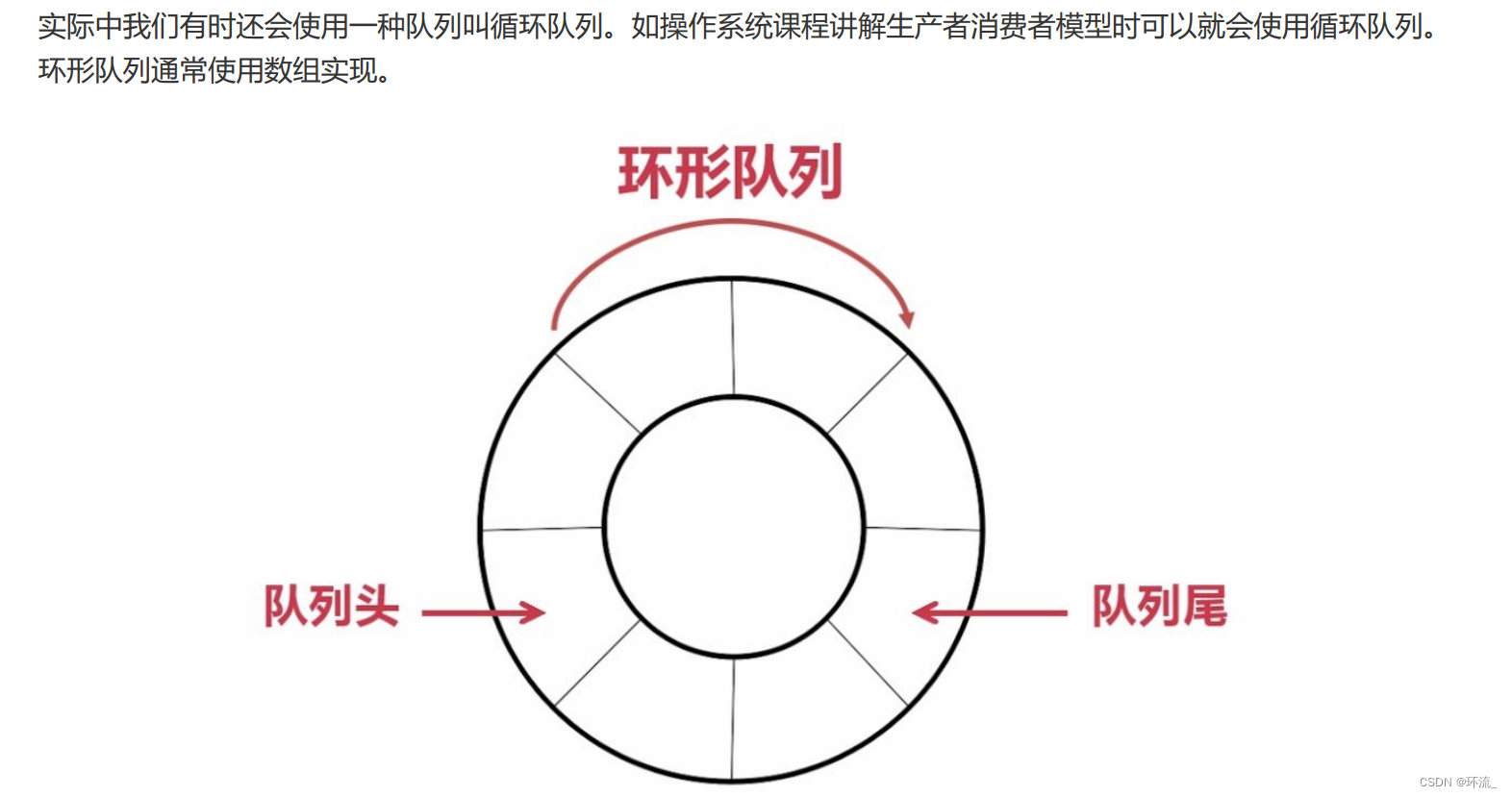
 （图片来源：比特高博）

循环队列一般使用数组来实现

循环队列，同样要先进先出嘛，那么给定你一个数组，我们现在要往数组里面入队了（放元素）

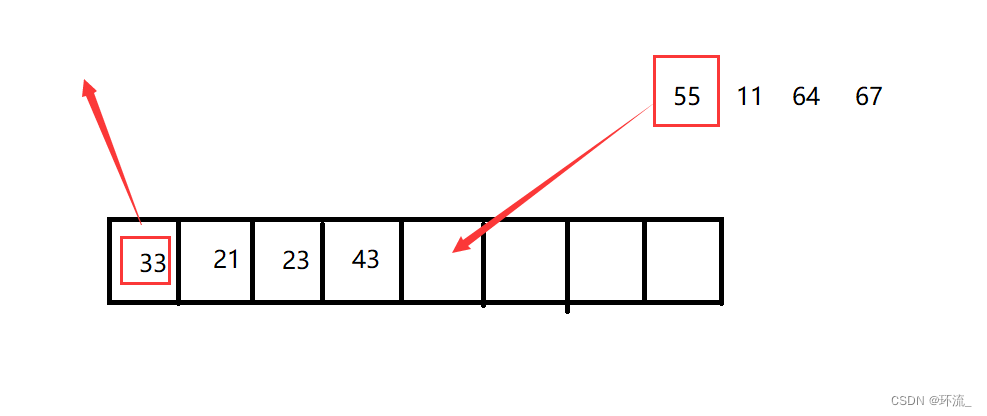
 但是我们可以放元素，也同样可以出元素对吧，我们要放入55，然后33出队，然后我们不仅放不仅出，最后元素会放到数组的最后位置

 

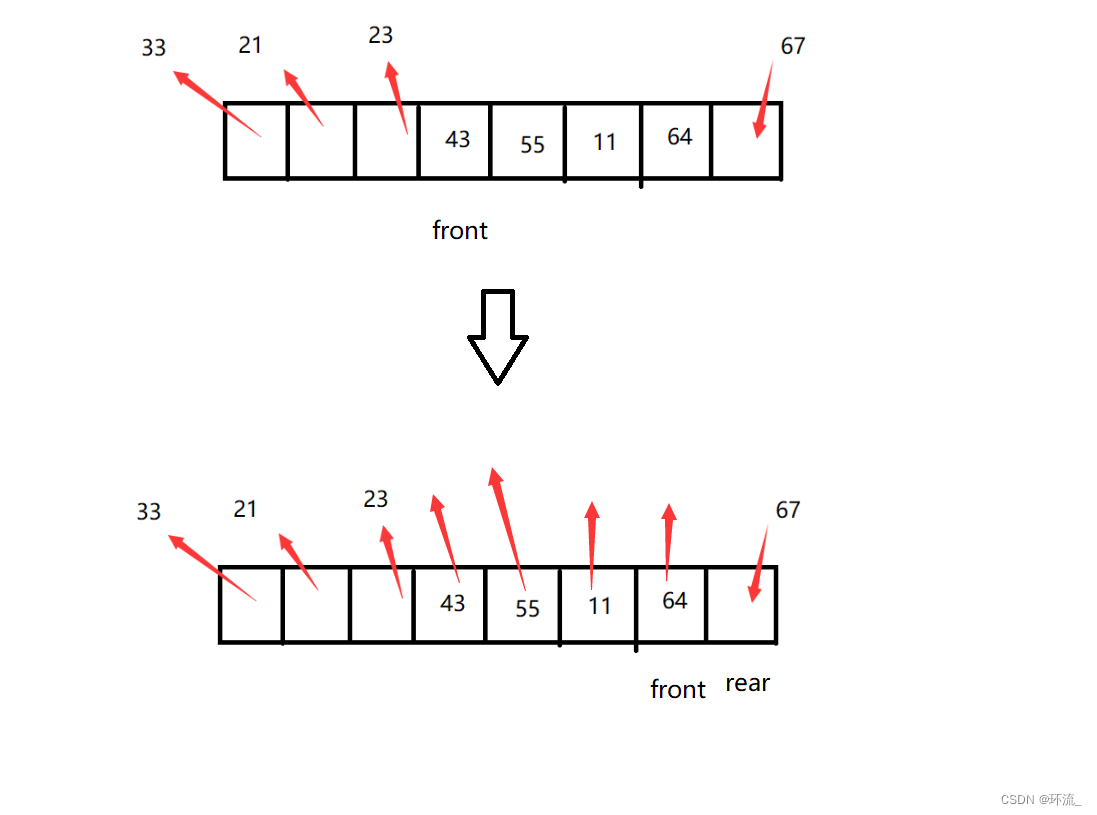
 我们现在front走到倒数第二个位置了，然后把67放入最后一个位置，rear++，为空，表示数组满了，但是我们发现，前面还存在我们之前出队元素的空间！！问题是你的rear还无法返回到0下标的空间

为了解决这个问题，我们把数组给卷起来看~

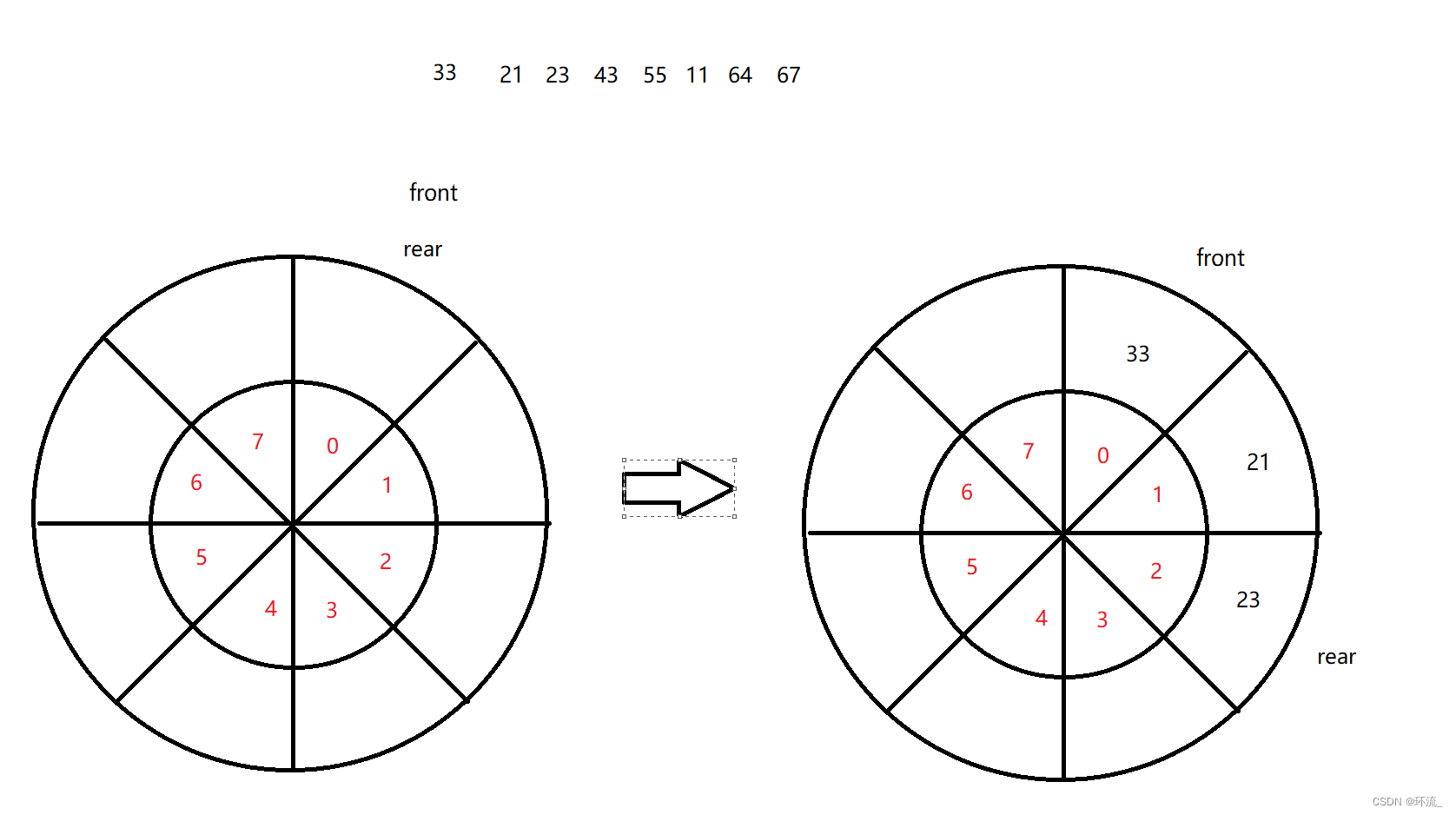
 我们把数组卷起来后，正常的往里面添加元素，刚开始front和rear相遇，表示数组为空，当我们不停的放入元素后，假设是一个循环（可以从7到0）

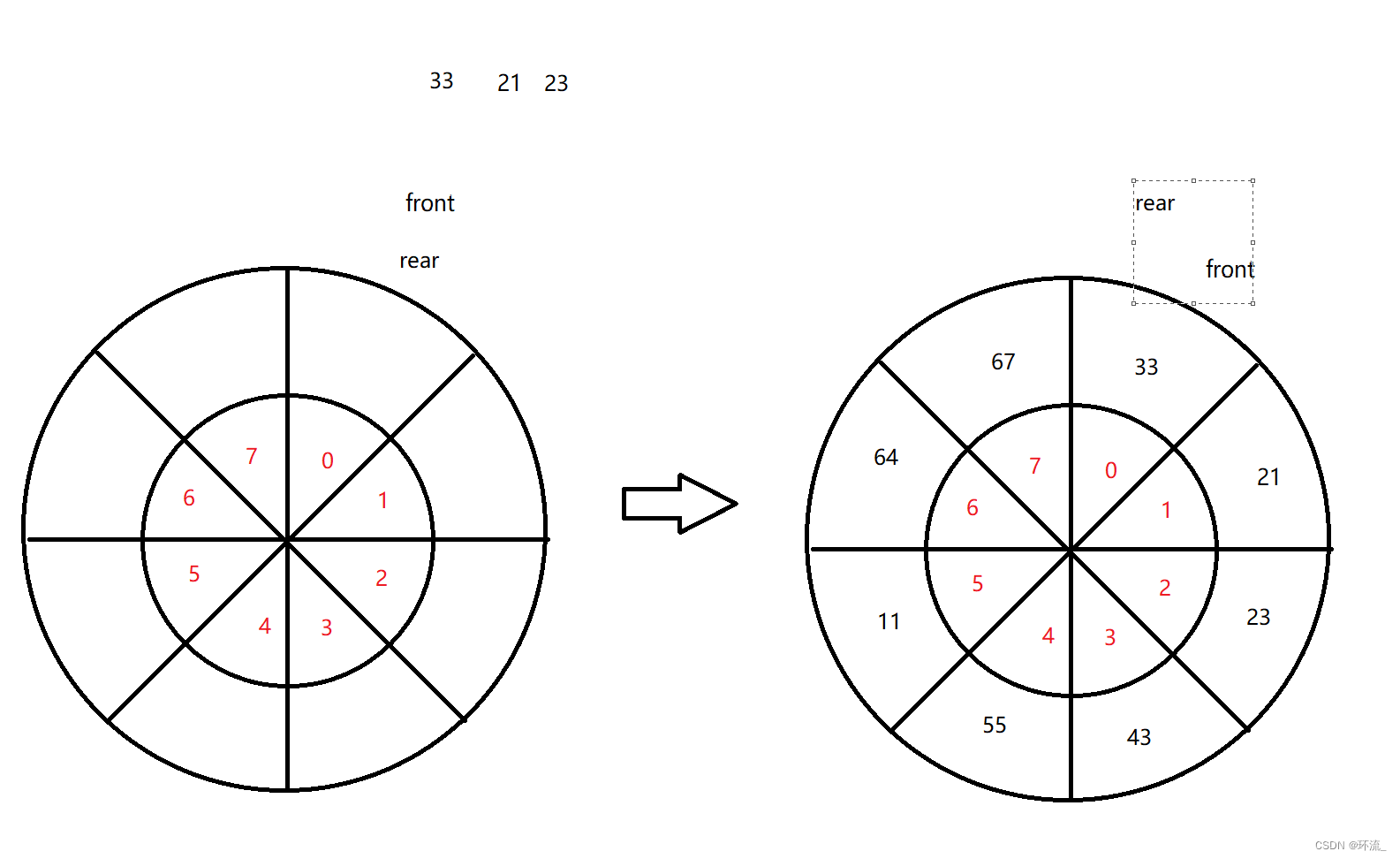
我们发现此时front又再次和rear相遇了，那么此时数组到底是空还是满呢？我们无法判断

为此我们有两种方法来判断当前数组是否为满

1.计数方法：这是最好的一个办法，我们定义一个usedSize来记录有效元素的个数，每当放入一个元素，计数器usedSize++，当usedSize的大小等于数组的大小的时候，我们就知道数组满了 

2.浪费空间法：当我们插入元素到6下标后，rear++会走到7，此时我们就要判断rear的下一个位置是否是0，如果为0，那么我们就不再对7下标位置插入元素，浪费掉这个空间，然后判定数组为满

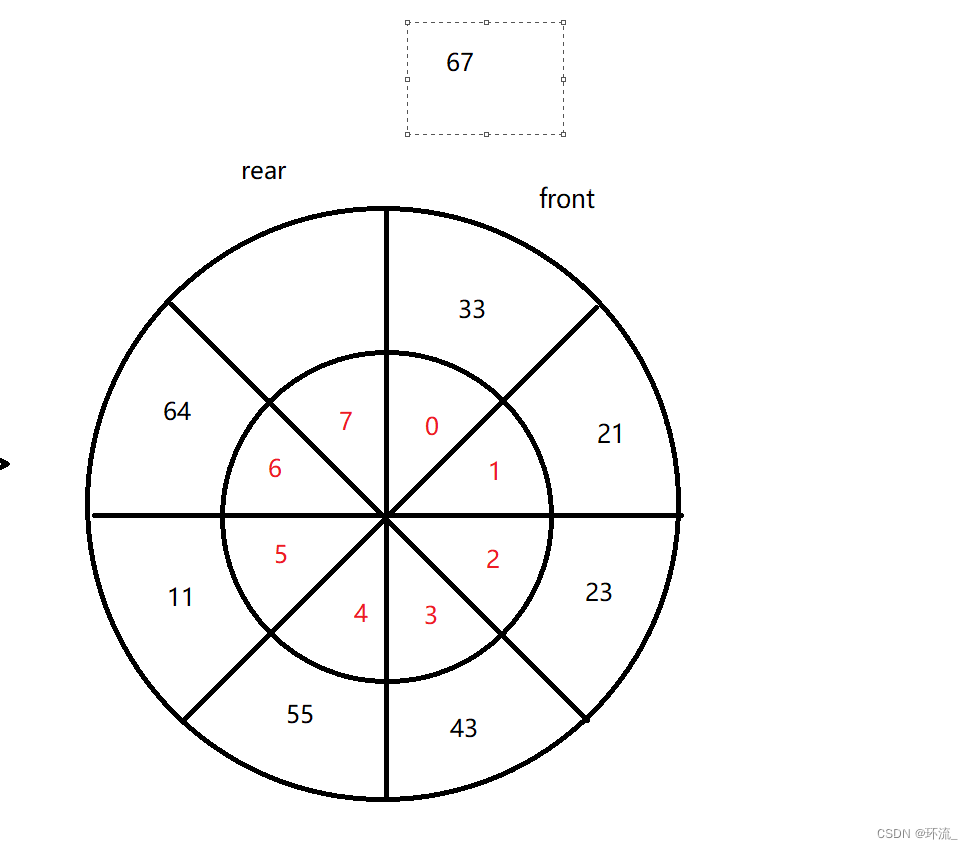
 计数器方法是最简单也是最好用的，只需要每次插入++一下就行了，接下来我们看看怎么浪费一个空间来实现这个循环队列

下面是代码展示

/**
 * 浪费空间的策略来设计循环队列
 */
public class MyCircularQueue {
    public int[] elem;
    //public int usedSize;计数
    public int front;//队头元素
    public int rear;//队尾元素

    public MyCircularQueue(int k){
        this.elem = new int[k+1];//数组初始化
    }
    //接下来是一堆方法

    /**
     * 入队
     * 要注意满的情况
     * 还要注意怎么从最后的下标跑到下标0从而实现循环的概念
     */
    public boolean enQueue(int value){
        if(isFull()){
            return false;
        }

        this.elem[rear] = value;
        //这里千万不能让rear++，要是++，你怎么从最后的下标跳到下标0？
        rear = (rear + 1) % elem.length;
        return true;
    }

    /**
     * 出队
     */
    public boolean deQueue(){
        if(isEmpty()){
            return false;
        }
        front = (front + 1) % elem.length;//这样才能循环
        return true;
    }

    /**
     * 获取队头元素
     * @return
     */
    public int Front(){
        if(isEmpty()){
            return -1;
        }
        return elem[front];
    }

    /**
     * 获取队尾元素
     * @return
     */
    public int Rear(){
        if (isEmpty()){
            return -1;
        }

        int index = (rear == 0) ? elem.length-1 : rear-1;
        return elem[index];
    }

    //判断满
    public boolean isFull(){
        return (rear + 1) % elem.length == 0;
    }

    //判断空
    public boolean isEmpty(){
        return front == rear;
    }
}

当我们每次插入元素的时候，我们不要让rear++，出元素的时候也不要直接让front++，如果直接让他们++，要怎么使7变到0从而完成循环效果？所以++是行不通滴，我们要使用一个式子

（当前位置+1）% 数组长度

假设现在rear在4下标位置，我们插入元素要4下标位置后，不能不让rear直接++到5的位置，而是 

（rear + 1） % len  =  （4+1）%8 = 5，我们发现rear正好到达5位置，那么我们想想我们插入7个元素后，此时rear在7位置下标，此时应该为满了，不能再插入了，因此当rear下一个位置是0下标的时候，就判断为满，使用上述这个式子，同样可以使rear过渡到0位置，（7+1）%8 = 0；

因此每次插入元素之前，都要判断是否为满，为空就是规定当front==rear的时候为空，因此每次删除元素的时候同样要去判断数组是否为空

当然，实现循环队列，还是那句话，使用计数器来实现是最好的（呜呜呜）

以上就是循环队列的实现和细节讲解