(一)递归概念
将复杂问题 递推分解为最简问题 然后将结果回归的过程Windows - LinuxLinux = Linux is not Unix使用方法: 自己调用自己
(二)斐波那契数列
兔子问题有一对大兔子 每个月繁衍 一对小兔子(一公一母)小兔子 每个月生长为 大兔子现有一对小兔子 一年后 有多少对?M1 1 AM2 1 A~M3 2 A->BM4 3 A->C + B~M5 5 A->D + B->E + C~M6 8 A->F + B->G + C->H + D~ + E~当前的所有兔子 = 上个月的所有兔子 + 这个月新生的兔子(可以繁衍的兔子)= 上个月的所有兔子数量 + 上上个月的所有兔子数量(经过了一个月的生长周期)Mn = M(n-1) + M(n-2)M5 = M4 + M3= (M3+M2) + (M2+M1)= (M2+M1 + M2) + (M2+M1)= 1+1+1 + 1+1 = 5M1=1 M2=1使用方式:1 )推导出递推公式 —— 找规律2 )找到递推的出口 —— 找出口
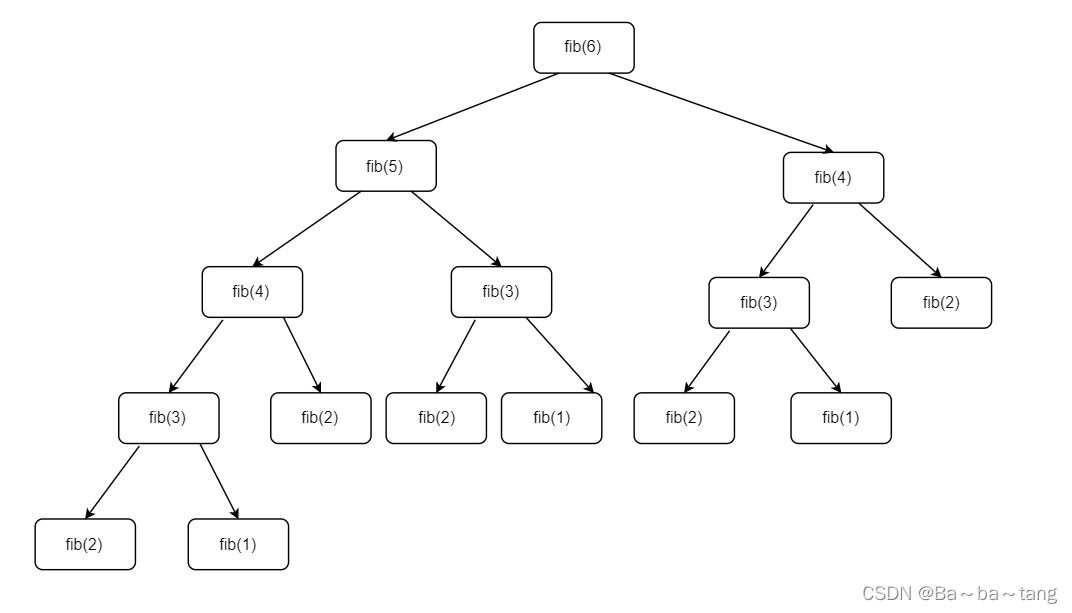
public static int fib(int N) {
if (N == 1) return 1;
if (N == 2) return 1;
System.out.println("求第" + N + "个月的兔子数量");
System.out.println("转化为求第" + (N - 1) + "个月和第" + (N - 2) + "个月的兔子数量");
return fib(N - 1) + fib(N - 2);
}
大部分递归
可以转化为迭代处理
Make it work,Make it right,Make it fast
思路:使用数组存储,通过
n-1
和
n-2
的值进行计算
public static int fib1(int N) {
// 6 —— 0 1 2 3 4 5
// fib(0) = 0 有时需要处理
if (N <= 1) return 1;
int[] arr = new int[N];
arr[0] = 1;
arr[1] = 1;
for (int i = 2; i < arr.length; i++) {
arr[i] = arr[i - 1] + arr[i - 2];
}
return arr[N - 1];
}
递归经典应用之汉诺塔
汉诺塔
印度的恒河 瓦拉那西 诞生婆罗门教放了三根柱子,其中一个根柱子上放了 64 个圆盘需要将全部圆盘 移动到另一根柱子上并且 每次只能移动一个 移动过程中 小圆盘必须在大圆盘之上为何不可完成?
分析:一个圆盘 A->C两个圆盘 A->B A->C B->C三个圆盘 A->C A->B C->B ( 把前两个圆盘 从 A 移动到 B)A->C ( 移动最大的圆盘 )B->A B->C A->C ( 再把前两个圆盘 从 B 移动到 C)N 个圆盘先把前 N-1 个圆盘 从 A 移动到 B ( 经由 C)再把最大的圆盘 从 A 移动到 C最后把前 N-1 个圆盘 从 B 移动到 C ( 经由 A)移动次数H(1) = 1H(2) = 3H(3) = H(2) + 1 + H(2) = 7H(4) = 7 + 1 + 7 = 15H(N) = H(N-1) + 1 + H(N-1) = 2^N - 1
// 四个参数 有n个圆盘 需要从A柱子移动到C 经由B
// 起始 中间 终点
public static void hanoi(int n, char A, char B, char C) {
// 出口
if (n == 1) {
System.out.println(A + "->" + C);
return;
}
// 先把前N-1个圆盘 从A移动到B (经由C)
// 再把最大的圆盘 从A移动到C
// 最后把前N-1个圆盘 从B移动到C (经由A)
hanoi(n - 1, A, C, B);
System.out.println(A + "->" + C);
hanoi(n - 1, B, A, C);
}public class Fibonacci {
public static void main(String[] args) {
System.out.println(fib1(6));
}
// 返回第n个月有多少只兔子
public static int fib(int N) {
if (N == 1) return 1;
if (N == 2) return 1;
System.out.println("求第" + N + "个月的兔子数量");
System.out.println("转化为求第" + (N - 1) + "个月和第" + (N - 2) + "个月的兔子数量");
return fib(N - 1) + fib(N - 2);
}
public static int fib1(int N) {
// 6 —— 0 1 2 3 4 5
// fib(0) = 0 有时需要处理
if (N <= 1) return 1;
int[] arr = new int[N];
arr[0] = 1;
arr[1] = 1;
for (int i = 2; i < arr.length; i++) {
arr[i] = arr[i - 1] + arr[i - 2];
}
return arr[N - 1];
}
}public class Hanoi {
public static void main(String[] args) {
//三个圆盘 A->C A->B C->B (把前两个圆盘 从A移动到B)
// A->C (移动最大的圆盘)
// B->A B->C A->C (再把前两个圆盘 从B移动到C)
hanoi(3, 'A', 'B', 'C');
}
// 四个参数 有n个圆盘 需要从A柱子移动到C 经由B
// 起始 中间 终点
public static void hanoi(int n, char A, char B, char C) {
// 出口
if (n == 1) {
System.out.println(A + "->" + C);
return;
}
// 先把前N-1个圆盘 从A移动到B (经由C)
// 再把最大的圆盘 从A移动到C
// 最后把前N-1个圆盘 从B移动到C (经由A)
hanoi(n - 1, A, C, B);
System.out.println(A + "->" + C);
hanoi(n - 1, B, A, C);
}
}