2.1 内存的工作原理

需要将数据存储到内存时，你请求计算机提供存储空间，计算机给你一个存储地址。

需要存储多项数据时，有两种基本方式——数组和链表。

2.2 数组和链表

有时候，需要在内存中存储一系列元素。

使用数组意味着所有待办事项在内存中都是相连的(紧靠在 一起的)。

现在假设你要添加第四个待办事项，但后面的那个抽屉放着别人的东西!

在这种情况 下，你需要请求计算机重新分配一块可容纳4个待办事项的内存，再将所有待办事项都移到那里。

同样，在数组中添加新元素也可能很麻烦。如果没 有了空间，就得移到内存的其他地方，因此添加新元素的速度会很慢。

一种解决之道是“预留座位”:即便当前只有3个待办事项，也请计算机提供10个位置，以防需要添加待办事项。这样，只要待办事项不超过10 个，就无需转移。

这是一个不错的权变措施，但它存在如下两个缺点：
你额外请求的位置可能根本用不上，这将浪费内存。你没有使用， 别人也用不了。
待办事项超过10个后，你还得转移。

对于这种问题，可使用链表来解决。

2.2.1 链表

链表中的元素可存储在内存的任何地方。

链表的每个元素都存储了下一个元素的地址，从而使一系列随机的内存地址串在一起。

在链表中添加元素很容易：只需将其放入内存，并将其地址存储到前一个元素中。

使用链表时，根本就不需要移动元素。

链表的优势在插入元素方面，那数组的优势又是什么呢?

2.2.2 数组

在需要读取链表的最后一个元素时，你不能直接读取，因为你不知道它所处的地址，必须先访问元素#1，从中获取元素 #2的地址，再访问元素#2并从中获取元素#3的地址，以此类推，直到访问最后一个元素。

需要同时读取所有元素时，链表的效率很高：你读取 第一个元素，根据其中的地址再读取第二个元素，以此类推。

但如果你需要跳跃，链表的效率真的很低。

数组与此不同：你知道其中每个元素的地址。

需要随机地读取元素时，数组的效率很高，因为可迅速找到数组的任何元素。

2.2.3 术语

数组的元素带编号，编号从0而不是1开始。

元素的位置称为索引 。

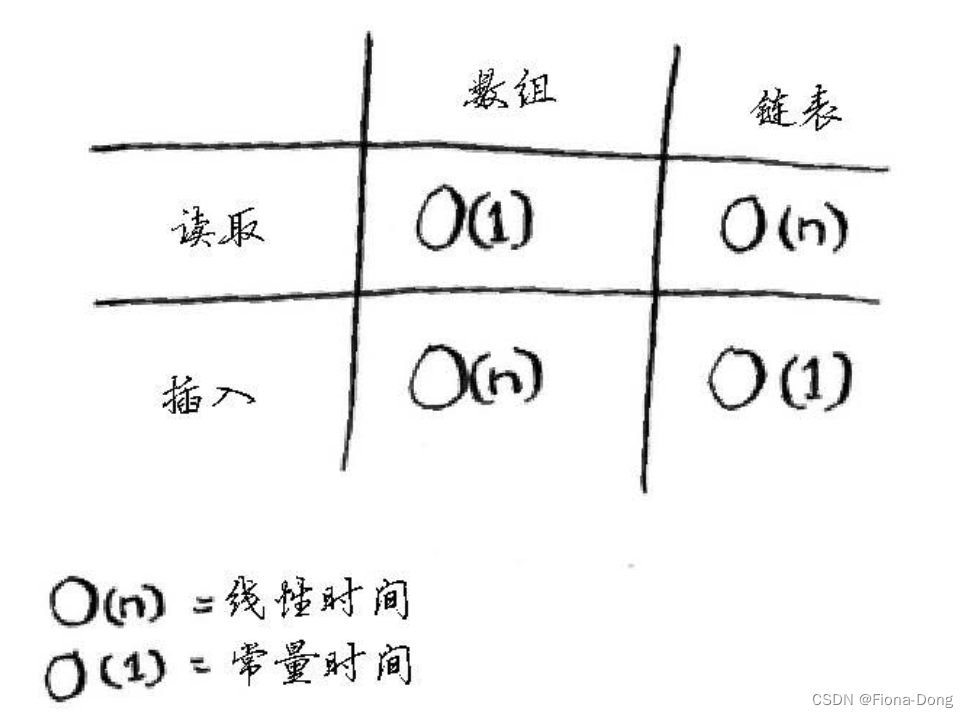
下面列出了常见的数组和链表操作的运行时间。

2.2.4 在中间插入

需要在中间插入元素时，数组和链表哪个更好呢?

使用链表时，插入元素很简单，只需修改它前面的那个元素指向的地址。

而使用数组时，则必须将后面的元素都向后移。如果没有足够的空间，可能还得将整个数组复制到其他地方!

因此，当需要在中间插入元素时，链表是更好的选择。

2.2.5 删除

如果你要删除元素呢?

链表也是更好的选择，因为只需修改前一个元素指向的地址即可。

而使用数组时，删除元素后，必须将后面的元素都向前移。

下面是常见数组和链表操作的运行时间。

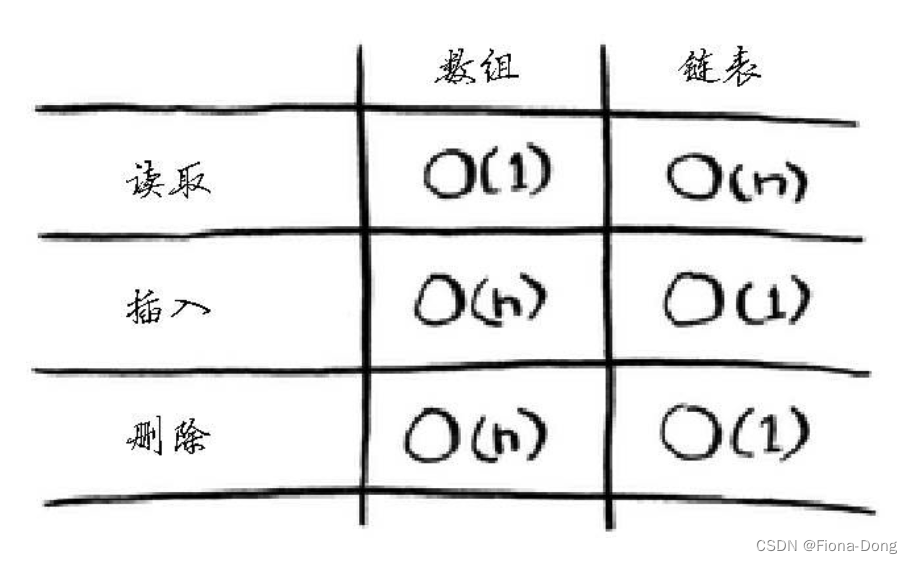
数组和链表哪个用得更多呢?

显然要看情况。但数组用得很多，因为它支持随机访问。

有两种访问方式：随机访问 和 顺序访问。顺序访问意味着从第一个元素开始逐个地读取元素。链表只能顺序访问。随机访问意味着可直接跳到第十个元素。

本书经常说数组的读取速度更快，这是因为它们支持随机访问。

很多情况都要求能够随机访问，因此数组用得很多。

2.3 选择排序

假设你的计算机存储了很多乐曲。对于每个乐队，你都记录了其作品被播放的次数。

你要将这个列表按播放次数从多到少的顺序排列，从而将你喜欢的乐队排序。该如何做呢?

一种办法是遍历这个列表，找出作品播放次数最多的乐队，并将该乐队添加到一个新列表中。再次这样做，找出播放次数第二多的乐队。继续这样做，你将得到一个有序列表。

要找出播放次数最多的乐队，必须检查列表中的每个元素。这需要的时间为O (n )。因此对于这种时间为O (n )的操作，你需要执行n 次。需要的总时间为 O (n × n )，即O ($n^2$)。

示例代码：

将数组元素按从小到大的顺序排列。先编写一个用于找出数组中最小元素的函数。
然后，使用这个函数来编写选择排序算法。

def findSmallest(arr):
    smallest = arr[0]
    smallest_index = 0
    for i in range(len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_index = i
    return smallest_index

def selectionsSort(arr):
    newArr = []
    for i in range(len(arr)):
        smallest = findSmallest(arr)
        newArr.append(arr.pop(smallest))
    return newArr

print(selectionsSort([5,3,6,2,10]))

References:
《 算法图解》—— 第2章 选择排序