图分类！！！

deepwalk

使用图中节点与节点的共现关系来学习节点的向量表示。那么关键的问题就是如何来描述节点与节点的共现关系，DeepWalk给出的方法是使用随机游走(RandomWalk)的方式在图中进行节点采样,RandomWalk是一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点，从其邻居中随机采样节点作为下一个访问节点，重复此过程，直到访问序列长度满足预设条件,获取足够数量的节点访问序列后，使用skip-gram model 进行向量学习。

deepwalk核心代码

DeepWalk算法主要包括两个步骤，第一步为随机游走采样节点序列，第二步为使用skip-gram modelword2vec学习表达向量。

①构建同构网络，从网络中的每个节点开始分别进行Random Walk 采样，得到局部相关联的训练数据；

②对采样数据进行SkipGram训练，将离散的网络节点表示成向量化，最大化节点共现，使用Hierarchical Softmax来做超大规模分类的分类器

同构网络（Homogeneous Network）是指所有节点在网络中具有相同功能的网络。在执行基本功能时，一个节点可以与其它节点互换。例如，固定电话网络中，每个电话对应网络中的一个节点，每个节点执行的功能基本上与其它任何节点相同。因此，电信网络通常是同质的。

LINE 算法原理

一种新的相似度定义

first-order proximity

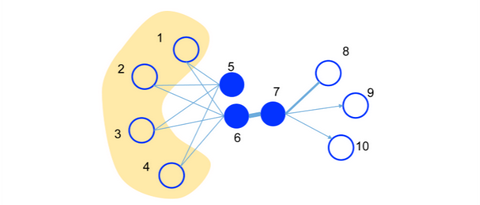
1阶相似度用于描述图中成对顶点之间的局部相似度，形式化描述为若 u , v 之间存在直连边，则边权 wuv 即为两个顶点的相似度，若不存在直连边，则1阶相似度为0。如上图，6和7之间存在直连边，且边权较大，则认为两者相似且1阶相似度较高，而5和6之间不存在直连边，则两者间1阶相似度为0。1st order 相似度只能用于无向图当中。

second-order proximity

仅有1阶相似度就够了吗？显然不够，如上图，虽然5和6之间不存在直连边，但是他们有很多相同的邻居顶点(1,2,3,4)，这其实也可以表明5和6是相似的，而2阶相似度就是用来描述这种关系的。形式化定义为，令 pu=(wu,1,...,wu,|V|) 表示顶点 u 与所有其他顶点间的1阶相似度，则 u 与 v 的2阶相似度可以通过 pu 和 pv 的相似度表示。若u与v之间不存在相同的邻居顶点，则2阶相似度为0。

Graph Embedding node2vec：算法原理，实现和应用

【Graph Embedding】node2vec：算法原理，实现和应用

](https://zhuanlan.zhihu.com/p/56380812)

node2vec是一种综合考虑DFS邻域和BFS邻域的graph embedding方法。简单来说，可以看作是deepwalk的一种扩展，是结合了DFS和BFS随机游走的deepwalk。

nodo2vec 算法原理

优化目标

设 f(u) 是将顶点 u 映射为embedding向量的映射函数,对于图中每个顶点u，定义 NS(u) 为通过采样策略 S 采样出的顶点 u 的近邻顶点集合。

node2vec优化的目标是给定每个顶点条件下，令其近邻顶点（如何定义近邻顶点很重要）出现的概率最大。

maxf∑u∈Vlog⁡Pr(NS(U)|f(u))

为了将上述最优化问题可解，文章提出两个假设：

条件独立性假设

假设给定源顶点下，其近邻顶点出现的概率与近邻集合中其余顶点无关。 Pr(Ns(u)|f(u))=∏ni∈Ns(u)Pr(ni|f(u))

特征空间对称性假设

这里是说一个顶点作为源顶点和作为近邻顶点的时候共享同一套embedding向量。(对比LINE中的2阶相似度，一个顶点作为源点和近邻点的时候是拥有不同的embedding向量的) 在这个假设下，上述条件概率公式可表示为 Pr(ni|f(u))=exp⁡f(ni)⋅f(u)∑v∈Vexp⁡f(v)⋅f(u)

根据以上两个假设条件，最终的目标函数表示为 maxf∑u∈V[−log⁡Zu+∑ni∈Ns(u)f(ni)⋅f(u)]

由于归一化因子 Zu=∑ni∈Ns(u)exp⁡(f(ni)⋅f(u)) 的计算代价高，所以采用负采样技术优化。

顶点序列采样策略

node2vec依然采用随机游走的方式获取顶点的近邻序列，不同的是node2vec采用的是一种有偏的随机游走。

给定当前顶点 v ，访问下一个顶点 x 的概率为

πvx 是顶点 v 和顶点 x 之间的未归一化转移概率， Z 是归一化常数。

node2vec引入两个超参数 p 和 q 来控制随机游走的策略，假设当前随机游走经过边 (t,v) 到达顶点 v 设 πvx=αpq(t,x)⋅wvx ， wvx 是顶点 v 和 x 之间的边权，

dtx 为顶点 t 和顶点 x 之间的最短路径距离。

下面讨论超参数 p 和 q 对游走策略的影响

Return parameter,p

参数p控制重复访问刚刚访问过的顶点的概率。注意到p仅作用于 dtx=0 的情况，而 dtx=0 表示顶点 x 就是访问当前顶点 v 之前刚刚访问过的顶点。那么若 p 较高，则访问刚刚访问过的顶点的概率会变低，反之变高。

In-out papameter,q

q 控制着游走是向外还是向内，若 q>1 ，随机游走倾向于访问和 t 接近的顶点(偏向BFS)。若 q<1 ，倾向于访问远离 t 的顶点(偏向DFS)。

下面的图描述的是当从 t 访问到 v 时，决定下一个访问顶点时每个顶点对应的 α 。

动态时间规整（DTW）算法简介

DTW最初用于识别语音的相似性。我们用数字表示音调高低，例如某个单词发音的音调为1-3-2-4。现在有两个人说这个单词，一个人在前半部分拖长，其发音为1-1-3-3-2-4；另一个人在后半部分拖长，其发音为1-3-2-2-4-4。

现在要计算1-1-3-3-2-4和1-3-2-2-4-4两个序列的距离（距离越小，相似度越高）。因为两个序列代表同一个单词，我们希望算出的距离越小越好，这样把两个序列识别为同一单词的概率就越大。

先用传统方法计算两个序列的欧几里得距离，即计算两个序列各个对应的点之间的距离之和。

距离之和 
= |A(1)-B(1)| + |A(2)-B(2)| + |A(3)-B(3)| + |A(4)-B(4)| + |A(5)-B(5)| + |A(6)-B(6)|
= |1-1| + |1-3| + |3-2| + |3-2| + |2-4| + |4-4|
= 6

如果我们允许序列的点与另一序列的多个连续的点相对应（相当于把这个点所代表的音调的发音时间延长），然后再计算对应点之间的距离之和。如下图：B(1)与A(1)、A(2)相对应，B(2)与A(3)、A(4)相对应，A(5)与B(3)、B(4)相对应，A(6)与B(5)、B(6)相对应。

这样的话，

距离之和
= |A(1)-B(1)| + |A(2)-B(1)| + |A(3)-B(2)| + |A(4)-B(2)| + |A(5)-B(3)| + |A(5)-B(4)| + |A(6)-B(5)| + |A(6)-B(6)| 
= |1-1| + |1-1| + |3-3| + |3-3| + |2-2| + |2-2| + |4-4| + |4-4|
= 0

我们把这种“可以把序列某个时刻的点跟另一序列多个连续时刻的点相对应”的做法称为时间规整（Time Warping）。

现在我们用一个6*6矩阵M表示序列A（1-1-3-3-2-4）和序列B（1-3-2-2-4-4）各个点之间的距离，M(i, j)等于A的第i个点和B的第j个点之间的距离，即

M(i,j)=|A(i)–B(j)|,1<=i,j<=6

我们看到传统欧几里得距离里对应的点：

A(1)-B(1)
A(2)-B(2)
A(3)-B(3)
A(4)-B(4)
A(5)-B(5)
A(6)-B(6)

它们正好构成了对角线，对角线上元素和为6。

时间规整的方法里，对应的点为：

A(1)A(2)-B(1)
A(3)A(4)-B(2)
A(5)-B(3)B(4)
A(6)-B(5)B(6)

这些点构成了从左上角到右下角的另一条路径，路径上的元素和为0。

因此，DTW算法的步骤为：

计算两个序列各个点之间的距离矩阵。
寻找一条从矩阵左上角到右下角的路径，使得路径上的元素和最小。

我们称路径上的元素和为路径长度。那么如何寻找长度最小的路径呢？

矩阵从左上角到右下角的路径长度有以下性质：

当前路径长度 = 前一步的路径长度 + 当前元素的大小
路径上的某个元素(i, j)，它的前一个元素只可能为以下三者之一：

a) 左边的相邻元素 (i, j-1) b) 上面的相邻元素 (i-1, j) c) 左上方的相邻元素 (i-1, j-1)

假设矩阵为M，从矩阵左上角(1,1)到任一点(i, j)的最短路径长度为Lmin(i, j)。那么可以用递归算法求最短路径长度：

起始条件：

Lmin(1,1)=M(1,1)

递推规则：

Lmin(i,j)=min{Lmin(i,j−1),Lmin(i−1,j),Lmin(i−1,j−1)}+M(i,j)

递推规则这样写的原因是因为当前元素的最短路径必然是从前一个元素的最短路径的长度加上当前元素的值。前一个元素有三个可能，我们取三个可能之中路径最短的那个即可。

struc2Vec

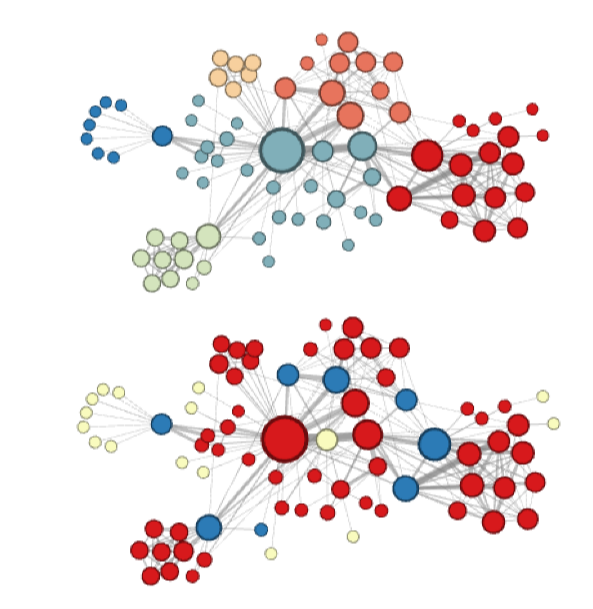
struc2vec可以看作是从另一个角度去抽取图上的某些特征，deepwalk学习的是近邻相似性，line学习的是一阶近邻和二阶近邻相似性，node2vec学习近邻相似性和结构相似性，但是node2vec其实无法学习到充分的结构相似性，因为bias random walk的步数毕竟是有限的，如果两个节点之间的距离非常远，则很难去学习到所谓的结构相似性，而struc2vec则是直接针对于结构相似性进行学习

相似度定义

Struc2Vec是从空间结构相似性的角度定义顶点相似度的。

用下面的图简单解释下，如果在基于近邻相似的模型中，顶点u和顶点v是不相似的，第一他们不直接相连，第二他们不共享任何邻居顶点。

而在struc2vec的假设中，顶点u和顶点v是具有空间结构相似的。他们的度数分别为5和4，分别连接3个和2个三角形结构，通过2个顶点(d,e;x,w)和网络的其他部分相连。

直观来看，具有相同度数的顶点是结构相似的，若各自邻接顶点仍然具有相同度数，那么他们的相似度就更高。

struc2vec使用层次结构来度量不同节点结构相似性，并构造一个多层图结构 M 来计算结构相似性并为节点生成embedding向量；

struc2vec认为，一个好的embdding表示应该能够反映两种信息：

1、具有相似社区结构的节点其embedding的结果要相近；

2、节点的结构相似性不依赖于节点或边的属性甚至是节点的标签信息

根据不同距离的邻居信息分别算出每个节点对的结构相似度，这涉及到了不同层次的结构相似度的计算，到这里就可以较好的理解层次化结构具体是什么意思了；

图片来自：https://zhuanlan.zhihu.com/p/63175042

2、构造一个加权多层图，其中网络中的所有节点都存在于每一层中（完全同一张图），并且每一层都对应于测量结构相似性时的层次结构存在级别上的差异。此外，每一层中每个节点对之间的edge权重与其结构相似度成反比；

3、使用多层图为每个节点生成上下文。特别是，多层图上的有偏随机游走（edge带权，不是完全随机游走的）用于生成节点序列，这个序列中很可能包括在结构上更相似的节点。

不得不说，这一步赞叹作者的脑洞，既然距离远结构相似的node无法直接通过在一张图上的游走得到，那么就构建多图，然后在图之间进行有偏游走，但是可以看到，这样的计算量是非常大的；

4、使用word2vec的方法对采样出的随机游走序列学习出每个节点的节点表示。

还有一个更好的图帮助理解，还是来自同一篇文章：

GraphSAGE

流程图：

采样：采样的例子，定为三个邻居节点，如果多了，就随机选择三个，如果少了，就从已有的节点全部选上，另外从中再次选择几个补上

聚合：均值聚合，lstm聚合（lstm本身是聚合的，但是通过将输入节点随机排列，是的lstm可以设用于无序的集合），pooling聚合

minbatch:GraphSAGE采用聚合邻居，和GCN使用全图方式，变成采样，这样在minbatch下，可以不使用全图信息，这使得在大规模上训练变得可行

第一步，按照要求k,s去选择节点，

GraphSAGE_embedding

训练的是GraphSAGE的权重参数w，经过GraphSAGE后，生成的embedding.,求loss，而不是直接生成节点的embedding

GAT(graph attention networks)

向往的GAT(图注意力网络的原理、实现及计算复杂度)

1 Graph Attention Networks的诞生

随着GCN的大红大紫（可以参考如何理解 Graph Convolutional Network（GCN）？），graph领域的deep learning研究可谓变得风生水起，人工智能又出现了新的网红。GCN在一系列任务取得了突破性进展的同时，一系列的缺点也逐渐被放大。

深度学习三巨头”之一的Yoshua Bengio组提出了Graph Attention Networks（下述简称为GAT）去解决GCN存在的问题并且在不少的任务上都取得了state of art的效果（可以参考机器之心：深入理解图注意力机制的复现结果），是graph neural network领域值得关注的工作。

2 聊点基础

登堂入室之前，先介绍三点基础问题。

2.1 Graph数据结构的两种“特征”

当我们说起graph或者network的数据结构，通常是包含着顶点和边的关系。研究目标聚焦在顶点之上，边诉说着顶点之间的关系。

对于任意一个顶点 i ，它在图上邻居 Ni ,构成第一种特征，即图的结构关系。

图1 graph示意图

当然，除了图的结构之外，每个顶点还有自己的特征 hi （通常是一个高维向量）。它可以使社交网络中每个用户的个体属性；可以是生物网络中，每个蛋白质的性质；还可以使交通路网中，每个交叉口的车流量。

graph上的deep learning方法无外乎就是希望学习上面的两种特征。

2.2 GCN的局限性

GCN是处理transductive任务的一把利器（transductive任务是指：训练阶段与测试阶段都基于同样的图结构），然而GCN有两大局限性是经常被诟病的：

（a）无法完成inductive任务，即处理动态图问题。inductive任务是指：训练阶段与测试阶段需要处理的graph不同。通常是训练阶段只是在子图（subgraph）上进行，测试阶段需要处理未知的顶点。（unseen node）

（b）处理有向图的瓶颈，不容易实现分配不同的学习权重给不同的neighbor。

2.3 Mask graph attention or global graph attention

还有一件事件需要提前说清楚：GAT本质上可以有两种运算方式的，这也是原文中作者提到的

Global graph attention

顾名思义，就是每一个顶点 i 都对于图上任意顶点都进行attention运算。可以理解为图1的蓝色顶点对于其余全部顶点进行一遍运算。

优点：完全不依赖于图的结构，对于inductive任务无压力

缺点：（1）丢掉了图结构的这个特征，无异于自废武功，效果可能会很差（2）运算面临着高昂的成本

Mask graph attention

注意力机制的运算只在邻居顶点上进行，也就是说图1的蓝色顶点只计算和橙色顶点的注意力系数。

3 GAT并不难懂

和所有的attention mechanism一样，GAT的计算也分为两步走：

3.1 计算注意力系数（attention coefficient）

对于顶点 i ，逐个计算它的邻居们（ j∈Ni ）和它自己之间的相似系数

eij=a([Whi||Whj]),j∈Ni(1)

解读一下这个公式：首先一个共享参数 W 的线性映射对于顶点的特征进行了增维，当然这是一种常见的特征增强（feature augment）方法；[⋅||⋅] 对于顶点 i,j 的变换后的特征进行了拼接（concatenate）；最后 a(⋅) 把拼接后的高维特征映射到一个实数上，作者是通过 single-layer feedforward neural network实现的。

显然学习顶点 i,j 之间的相关性，就是通过可学习的参数 W 和映射 a(⋅) 完成的。

有了相关系数，离注意力系数就差归一化了！其实就是用个softmax

αij=exp(LeakyReLU(eij))∑k∈Niexp(LeakyReLU(eik))(2)

要注意这里作者用了个 LeakyReLU(⋅) ，至于原因嘛，估计是试出来的，毕竟深度玄学。

上面的步骤可以参考图2进行理解

图2 第一步运算示意图

3.2 加权求和（aggregate）

完成第一步，已经成功一大半了。第二步很简单，根据计算好的注意力系数，把特征加权求和（aggregate）一下。

hi′=σ(∑j∈NiαijWhj)(3)

hi′ 就是GAT输出的对于每个顶点 i 的新特征（融合了邻域信息）， σ(⋅) 是激活函数。

式（3）看着还有点单薄，俗话说一个篱笆三个桩，attention得靠multi-head帮！来进化增强一下

hi′(K)=||k=1Kσ(∑j∈NiαijkWkhj)(4)

嗯，这次看起来就很健壮了，multi-head attention也可以理解成用了ensemble的方法，毕竟convolution也得靠大量的卷积核才能大显神威！

上面的步骤可以参考图3进行理解

图3 第二步运算示意图

4 GAT的代码实现

上面的内容已经介绍了GAT模型的基本原理，在代码实现方面，下面的文章讲解得比较详细，感觉兴趣的朋友可以参考。

木盏：【GNN】图注意力网络GAT(含代码)657 赞同 · 95 评论文章编辑

5 GAT的计算复杂度

下面来推导一下单头GAT模型的计算复杂度，为了与主流文献中的介绍保持一致，用 |V| 表示图中的顶点数， |E| 表示图中的边数， F 表示原始的特征维度， F′ 表示输出的特征维度。

计算复杂度是由运算中的乘法次数决定的，从上面的公式(1)-(4)可以看出，GAT的运算主要涉及如下两个乘法运算环节：

顶点的特征映射，即Whi 将F 维的向量hi映射到F′维的空间， W 是 F×F′ 维的参数矩阵。因此， Whi 的计算复杂度是 O(F×F′) 。对于所有顶点的特征都需要进行映射，则计算复杂度为 O(|V|×F×F′)
计算注意力系数过程中的 a(⋅) 映射，从公式(1)可以看出，a(⋅) 是将 2×F′ 维的向量映射到一个实数上，则其计算复杂度为 O(F′) 。在计算注意力系数的过程中，图有多少条边，就需要计算多少次（因为每个顶点计算与其邻居顶点的相似系数），则其计算复杂度为 O(|E|×F′)

结合上面两个环节，GAT模型首先计算所有顶点的特征映射，然后计算注意力系数，后续的aggregate环节中主要都是加权求和运算，不再涉及高复杂度的乘法运算了。因此，单头GAT模型的计算复杂度为 O(|V|×F×F′)+O(|E|×F′) ，而多头（multi-head）情形下的计算复杂度就是单头的 K （ K 是head数）倍。

6 谈几点深入的理解

6.1 与GCN的联系与区别

无独有偶，我们可以发现本质上而言：GCN与GAT都是将邻居顶点的特征聚合到中心顶点上（一种aggregate运算），利用graph上的local stationary学习新的顶点特征表达。不同的是GCN利用了拉普拉斯矩阵，GAT利用attention系数。一定程度上而言，GAT会更强，因为顶点特征之间的相关性被更好地融入到模型中。