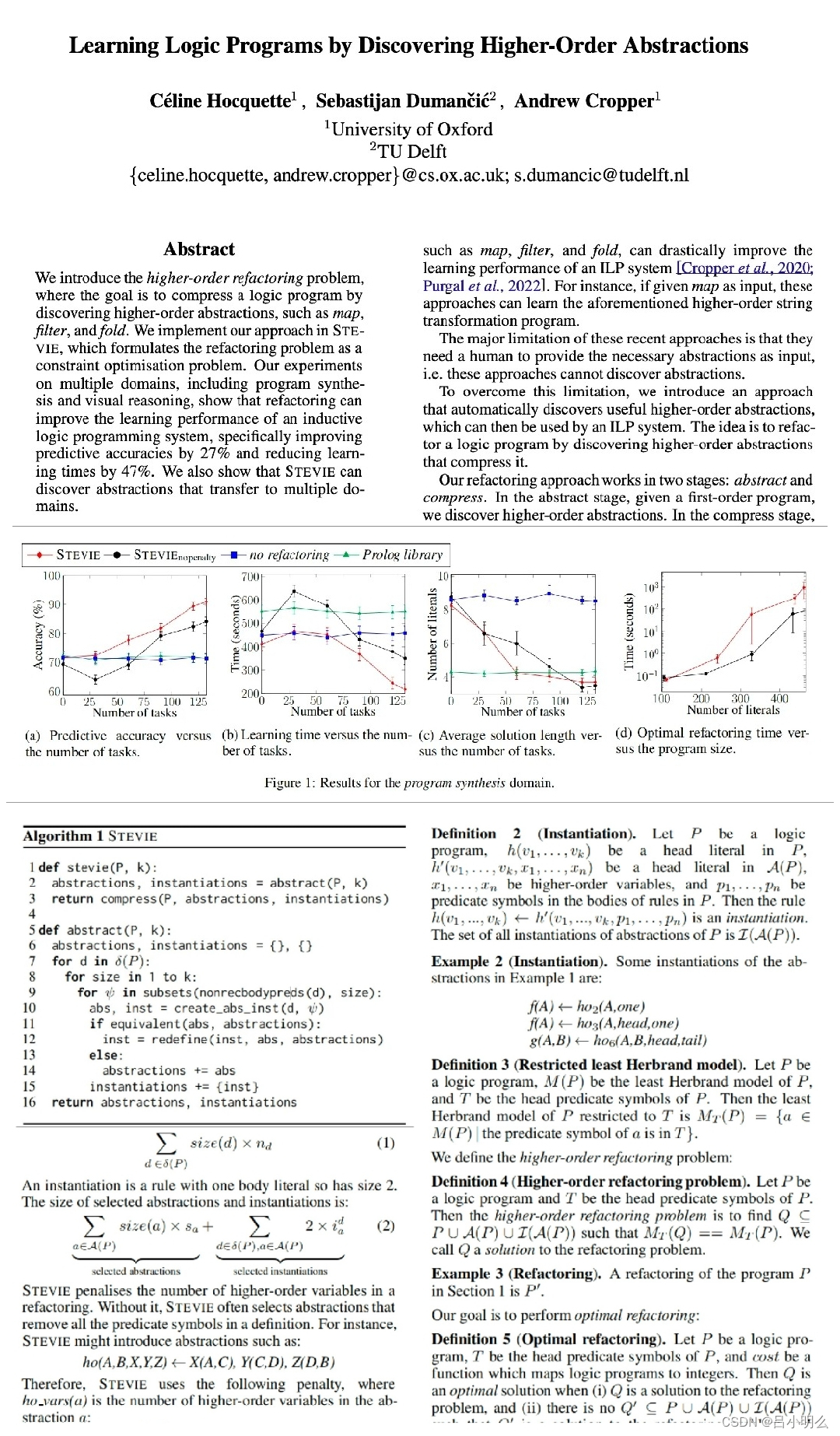
Multiagent Environments
In multiagent environments, each agent must:
— Consider everyone else’s actions
— Coordinate in order to act coherently
多个智能体(agent)相互作用,每个智能体都具有自己的目标和行动策略。在多智能体环境中,智能体需要考虑其他智能体的行动,并协调一致以采取有效的行动。
“Games” 博弈
• Game theory views any multiagent system as “game“
• Most commonly studied games in AI are called
— Deterministic 确定性博弈是指博弈中每个智能体的行动都是确定性的,不存在随机性。
— Turn-taking (agents act alternately) 博弈中智能体交替行动
— Two-player 博弈中只有两个智能体参与,每个智能体都在自己的回合中做出决策。
— Zero-sum (individual utility is always equal and opposite)博弈中每个智能体的收益之和为零
— Perfect Information (fully observable) 完全信息博弈是指博弈中每个智能体都知道其他智能体的所有信息,包括他们的策略和收益。
Defining Games
• Two Standard Representations:
— Normal Form: (a.k.a. Matrix Form, Strategic Form)
List what payoffs get as a function of their actions
◦ It is as if players moved simultaneously
◦ But strategies encode many things
在正常形式中,每个玩家根据自己的行动获得支付,这些支付以矩阵的形式表示。
类似于玩家同时行动,但实际上策略包含了许多信息。
— Extensive Form: includes timing of moves
◦ Players move sequentially, represented as a tree
◦ Keeps track of what each player knows when they make each decision
玩家按顺序移动,这些移动以树状结构表示。
扩展形式可以追踪每个玩家在做出每个决策时所知道的信息。


• An extensive form game is defined as a search problem with the following elements:
— S0: initial state
— Player (s): which player moves at state s
— Actions(s): what are the actions available at state s
— Result(s, a): transition model
— Terminal Test(s): true when the game is over, defines terminal states
— Utility(s, p): utility function (or payoff) for player p at terminal state s
(in zero sum games Utility(s, p1) = −Utility(s, p2))