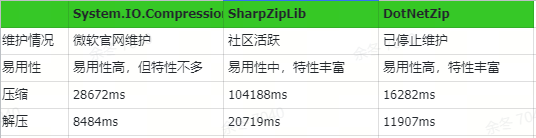
本篇内容节选自今年初我撰写的那篇10万的文章《融合RL与LLM思想，探寻世界模型以迈向AGI》，其观点也是文章中核心中的核心。

想进一步完整阅读电子版的伙伴大家可关注评论联系我，节选内容如下↓

“...存在一个大的开放的tokenization世界。

在这个世界中存在着可用token泛化表征的多种模式链（pattern chain），其映射结构或者可等效于tokenize世界中存在着自然且合理的token间单跳或多跳映射的分布·distribution或模式链·pattern chain的构象。

这里所说的token间单或多跳映射的分布或pattern chain的构象直觉上可 以当前微分拓扑学和数据科学中的数据流形分布或流形嵌入等相关理论来进行抽象表述。- 这部分相关观点大家也可以参考顾险峰教授的跨领域学科「计算共形几何」中相关的理论描述。

同时，流形在某种程度上又能很好的体现出高维到低维分布的泛化性，表征分布与映射下的结构稳定性与连续性。

进一步延展的思路是：结合AIGC的当下，是否可将上述数据科学中的数据流形分布概念扩展到认知科学中的认知流形分布呢？- 我想对于一张人脸图像的多“像素”数据分布与一项多“步骤”复杂推理和决策的认知过程链其所映射出的“流形构象”在数学抽象上是等价的。

而流形下的“distribution”或离散形式化出的“pattern chain”则通过tokenize在理念世界中表征并并泛化了真实世界的各种现象和抽象规律。

这个规律包含了在人类看来简单似直觉的可通过系统·Ⅰ 单跳映射的pattern，也囊括了复杂的需通过系统·Ⅱ 多跳映射的pattern（但这里需要注意，在现实世界中不同的认知层级下这种复杂的多跳推理映射也多有强行转化提炼为基于直觉的单层pattern映射，但猜想这样的pattern转换在世界中的泛化性分布可能会受到改变和一定的影响）。

简单的pattern可包括语言的问答交互，交互过程中的直觉反馈，直觉包括简单的结论性先验知识、生物的行动与决策反射..

复杂的pattern chain包括数学、物理学、生物学的定理证明过程中的演绎与归纳，庞杂而完备的理论(theory)体系，复杂的工程架构，多步骤的生物过程和思维过程..

...”