哈希表的封装和位图

news2025/1/10 3:06:14

文章目录

  • 2 封装
    • 2.1 基础框架
    • 2.2 迭代器(1)
    • 2.3 迭代器(2)
  • 3. 位图
    • 3.1 问题引入
    • 3.2 左移和右移？
    • 3.3 位图的实现
    • 3.4 位图的题目
    • 3.5 位图的应用

2 封装

2.1 基础框架

文章

有了前面map和set封装的经验，容易写出下面的代码

// UnorderedSet.h
#pragma once
#include "HashTable.h"
template <class K, class Hash = HashFunc<K>>
class UnorderedSet
{
	// 返回key
	struct SetKeyOfT
	{
		const K& operator()(const K& key)
		{
			return key;
		}
	};
public:
	bool insert(const K& key)
	{
		return _ht.Insert(key);
	}
private:
	HashTable<K, K, SetKeyOfT, Hash> _ht;
};

// UnorderedMap.h
#pragma once
#include "HashTable.h"
template <class K, class V,  class Hash = HashFunc<K>>
class UnorderedMap
{
	// 返回pair的first,即key
	struct MapKeyOfT
	{
		const K& operator()(const pair<K, V> &kv)
		{
			return kv.first;
		}
	};
public:
	bool insert(const pair<K, V>& kv)
	{
		return _ht.Insert(kv);
	}
	
private:
	HashTable<K, pair<K, V>, MapKeyOfT, Hash> _ht;
};

// HashTable.h
template <class T>
struct HashNode
{
	HashNode(const T& data)
		: _data(data)
		, _next(nullptr)
	{}
	HashNode* _next;
	T _data;
};
// UnorderedMap->HashTable<K, pair<K, V>>
// UnorderedSet->HashTable<K, K>
template <class K, class T, class KeyOfT , class Hash>
class HashTable
{
	typedef HashNode<T> Node;
public:
	// ...
	bool Insert(const T& data)
	{
		// 如果已经有该元素了，返回false
		if (Find(kot(data)))	return false;
		size_t sz = _table.size();
		// 负载因子设置到1
		if (_table.size() == _n)
		{
			size_t newSz = sz * 2;
			vector<Node*> newTable;
			newTable.resize(newSz, nullptr);

			for (size_t i = 0; i < sz; ++i) {
				Node* cur = _table[i];
				while (cur) {
					Node* next = cur->_next;
					size_t hashI = hf(kot(cur->_data)) % newSz;
					// 头插到新链表
					cur->_next = newTable[hashI];
					newTable[hashI] = cur;
					cur = next;
				}
				_table[i] = nullptr;
			}
			_table.swap(newTable);
		}

		size_t hashI = hf(kot(data)) % sz;
		Node* newNode = new Node(data);
		// 头插
		newNode->_next = _table[hashI];
		_table[hashI] = newNode;
		++_n;
		return true;
	}
	// ...
private: 
	vector<Node*> _table;
	size_t _n;
	Hash hf;
	KeyOfT kot;
};

其中HashTable.h中部分代码已经省略，详细见文章

2.2 迭代器(1)

写法1

// HashTable.h
template <class T>
struct __HTIterator
{
	typedef HashNode<T> Node;
	typedef __HTIterator<T> Self;
	Node* _node;
	vector<Node*>& _table;	// 方便找下一个桶
	size_t _hashI;		// 当前找到哪个桶了

	__HTIterator(Node* node, vector<Node*>& table, size_t hashI)
		: _node(node)
		, _table(table)
		, _hashI(hashI)
	{}

	Self& operator++()
	{
		if (_node->_next) {
			// 当前桶还有节点，走到下一个节点
			_node = _node->_next;
		}
		else {
			// 当前桶没有节点了，去找下一个桶
			++_hashI;
			while (_hashI < _table.size()) {
				if (_table[_hashI] != nullptr) {
					// 找到了非空节点
					_node = _table[_hashI];
					break;
				}
				++_hashI;
			}
			// 没有下一个有节点的桶了
			if (_hashI == _table.size()) {
				_node = nullptr;	// 让nullptr充当end()
			}
		}
		return *this;
	}

	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}

	T& operator*()
	{
		return _node->_data;
	}

	T* operator->()
	{
		return &(_node->_data);
	}
};

template <class K, class T, class KeyOfT , class Hash = HashFunc<K>>
class HashTable
{
    // ...
    typedef __HTIterator<T> Iterator;
	Iterator begin()
    {
        // 找到第一个有存值的桶，传给迭代器
        for (size_t i = 0; i < _table.size(); i++) {
            if (_table[i] != nullptr) {
                return Iterator(_table[i], _table, i);
            }
        }
        // 找到最后还没有找到，证明是空哈希表
        return end();
    }
    
    Iterator end()
    {
        return Iterator(nullptr, _table, -1);
    }
  	// ...
}

2.3 迭代器(2)

// 因为后面的__HTIterator使用了HashTable这个类，向上找找不到，所以需要前置声明
template <class K, class T, class KeyOfT, class Hash>
class HashTable;

template <class K, class T, class KeyOfT, class Hash>
struct __HTIterator
{
	typedef HashNode<T> Node;
	typedef __HTIterator<K, T, KeyOfT, Hash> Self;
	Node* _node;
	HashTable<K, T, KeyOfT, Hash>* _ht;	// 方便找下一个桶
	size_t _hashI;		// 当前找到哪个桶了

	__HTIterator(Node* node, HashTable<K, T, KeyOfT, Hash>* ht, size_t hashI)
		: _node(node)
		, _ht(ht)
		, _hashI(hashI)
	{}

	Self& operator++()
	{
		if (_node->_next) {
			// 当前桶还有节点，走到下一个节点
			_node = _node->_next;
		}
		else {
			// 当前桶没有节点了，去找下一个桶
			++_hashI;
			while (_hashI < _ht->_table.size()) {
				if (_ht->_table[_hashI] != nullptr) {
					// 找到了非空节点
					_node = _ht->_table[_hashI];
					break;
				}
				++_hashI;
			}
			// 没有下一个有节点的桶了
			if (_hashI == _ht->_table.size()) {
				_node = nullptr;	// 让nullptr充当end()
			}
		}
		return *this;
	}

	// ...
};

template <class K, class T, class KeyOfT, class Hash>
class HashTable
{
	typedef HashNode<T> Node;
	template <class K, class T, class KeyOfT, class Hash>
	friend struct __HTIterator;		// 让__HTIterator成为HashTable的友元，因为用到了_table这个私有属性
public:
    
	typedef __HTIterator<K, T, KeyOfT, Hash> Iterator;
    Iterator begin()
    {
        // 找到第一个有存值的桶，传给迭代器
        for (size_t i = 0; i < _table.size(); i++) {
            if (_table[i] != nullptr) {
                return Iterator(_table[i], this, i);
            }
        }
        // 找到最后还没有找到，证明是空哈希表
        return end();
    }

    Iterator end()
    {
        return Iterator(nullptr, this, -1);
    }
    // ...
}

const迭代器不再实现，太复杂了。

3. 位图

概念：所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在的。

3.1 问题引入

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。

  1. 遍历，时间复杂度O(N)

  2. 排序(O(NlogN))，利用二分查找: logN

  3. 数据是否在给定的整形数据中，结果是在或者不在，刚好是两种状态，那么可以使用一个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0代表不存在。比如：

​ image-20240908131159204

可以计算一下，40亿个数，需要开2^32bit，即512MB

3.2 左移和右移？

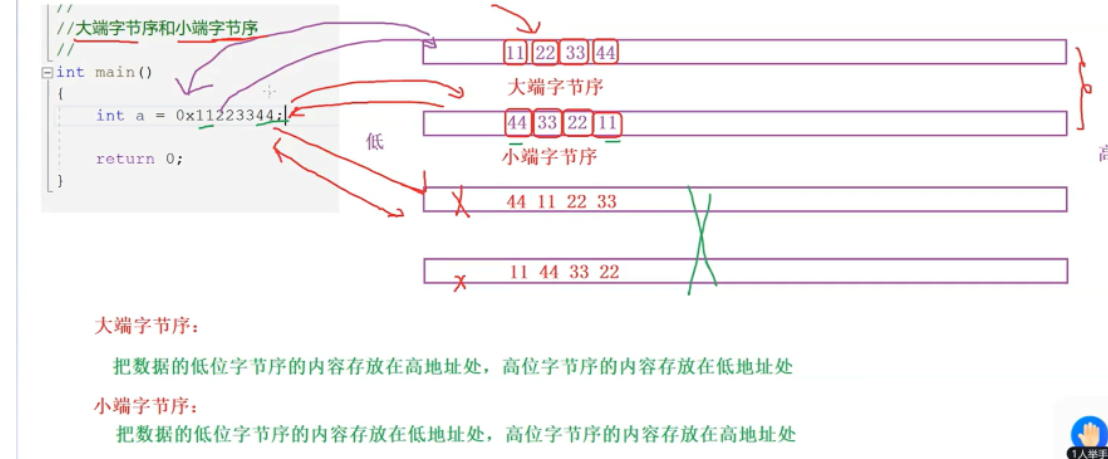
image-20240908154458368

vs是以小端字节序存储的，左移指的是像高地址移动，右移是指向低地址移动，并不是按移动的方向定义的

执行完i = 1

image-20240908155207271

执行完i <<= 8

image-20240908155231047

image-20240908155547251

3.3 位图的实现

// N表示需要多少bit位
template<size_t N>
class MyBitset
{
public:
	MyBitset()
	{
		_bits.resize(N / 32 + 1, 0);
	}

	/*把x映射的位置1
	* x在数组的第几个整形呢？		i = x / 32
	* x在这个整形的第几个位呢？   j = x % 32*/ 
	void set(size_t x) 
	{
		size_t i = x / 32;
		size_t j = x % 32;
		// 或等上1<<j
		_bits[i] |= (1 << j);
	}

	// 把x映射的位置0
	void reset(size_t x)
	{
		size_t i = x / 32;
		size_t j = x % 32;
		// 与等上~(1<<j)
		_bits[i] &= (~(1 << j));
	}

	// 检查x所在的bit是0还是1
	bool test(size_t x)
	{
		size_t i = x / 32;
		size_t j = x % 32;
		// 与上1
		return _bits[i] & (1 << j);
	}
private:
	vector<size_t> _bits;
};

image-20240908162435739

上面的3.1的问题，我们可以开一个bitset来解决

// solution 1
MyBitset<0xffffffff> bs;
// solution 2
MyBitset<-1> bs2;

3.4 位图的题目

  1. 给定100亿个整数，设计算法找到只出现一次的整数？

使用两个bitset，00表示出现0次，01表示出现1次，10表示出现2次或者2次以上

template<size_t N>
class TwoBitset
{
public:
	/*
	* 00->01
	* 01->10
	* 10->same
	*/
	void set(size_t x)
	{
		if (!_bs1.test(x) and !_bs2.test(x)) {
			_bs2.set(x);
		}
		else if (!_bs1.test(x) and _bs2.test(x)) {
			_bs1.set(x);
			_bs2.reset(x);
		}
	}

	/* 打印出现一次的数字 */
	void PrintOnce()
	{
		for (size_t i = 0; i < N; i++) {
			if (!_bs1.test(i) and _bs2.test(i))
				cout << i << ' ';
		}
		cout << endl;
	}

private: 
	MyBitset<N> _bs1;
	MyBitset<N> _bs2;
};
  1. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

与上面类似：将这些整数各自映射到一个位图，一个值在两个位图都存在，则是交集

  1. 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

也是一样，两个位图，00表示出现0次，01表示出现1次，10表示出现2次，11表示出现3次及以上

3.5 位图的应用

  1. 快速查找某个数据是否在一个集合中
  2. 排序 + 去重
  3. 求两个集合的交集、并集等
  4. 操作系统中磁盘块标记

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2116168.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

WireShark抓包软件介绍和安装

WireShark抓包软件介绍和安装

文章目录 一、WireShark软件介绍1. **概述**2. **主要功能**3. **使用场景**4. **安装和使用**5. **优点和限制**6. **结论** 二、WireShark的安装三、WireShark的基本使用1. **混杂模式&#xff08;Promiscuous Mode&#xff09;****概述****工作原理****应用场景****启用方式…
阅读更多...
STM32F407VET6开发板RT-Thread memheap 内存堆的适配

STM32F407VET6开发板RT-Thread memheap 内存堆的适配

相关文章 STM32F407VET6开发板RT-Thread的移植适配 STM32F407VET6开发板RT-Thread MSH 串口的适配 环境 STM32F407VET6 开发板&#xff08;魔女&#xff09;&#xff0c;http://www.stm32er.com/ Keil MDK5&#xff0c;版本 5.36 memheap 内存堆 RT-Thread 支持 memheap …
阅读更多...
数据结构基础讲解（二）——线性表之单链表专项练习

数据结构基础讲解（二）——线性表之单链表专项练习

本文数据结构讲解参考书目&#xff1a; 通过网盘分享的文件&#xff1a;数据结构 C语言版.pdf 链接: https://pan.baidu.com/s/159y_QTbXqpMhNCNP_Fls9g?pwdze8e 提取码: ze8e 上一节我讲了线性表中顺序表的定义以及常用的算法&#xff0c;那么这节我将继续讲解顺序表中的链式…
阅读更多...
MySQL-CRUD入门1

MySQL-CRUD入门1

文章目录 认识配置文件client节点mysql节点mysqld节点 数据的添加(Create)添加一行数据添加多行数据两种添加数据的效率对比 数据的查询(Retrieve)全列查询指定列查询查询中带有表达式关于字面量关于as重命名 临时表引入distinct去重order by 排序关于NULL 认识配置文件 在我们…
阅读更多...
数据结构基础详解(C语言): 树与二叉树的应用_哈夫曼树与哈夫曼曼编码_并查集_二叉排序树_平衡二叉树

数据结构基础详解(C语言): 树与二叉树的应用_哈夫曼树与哈夫曼曼编码_并查集_二叉排序树_平衡二叉树

文章目录 树与二叉树的应用1.哈夫曼树与哈夫曼曼编码1.1 带权路径长度1.2 哈夫曼树1.2.1 哈夫曼树的构造1.3 哈夫曼编码 2.并查集2.1 并查集的三要素2.1.1 并查集的逻辑结构2.1.2 并查集的存储结构 2.2 并查集的优化2.2.1 初步优化&#xff08;并操作优化&#xff09;2.2.2 终极…
阅读更多...
flink wordcount

flink wordcount

Maven配置pom文件 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/P…
阅读更多...
mybatis-plus使用@EnumValue搭配shardingsphere报错“getObject with type”

mybatis-plus使用@EnumValue搭配shardingsphere报错“getObject with type”

目录 一、背景二、修改方案三、如何让修改的TypeHandler生效1、在TableField中配置TypeHandler2、考虑直接在TypeHandlerRegistry注册该枚举的handler为自定义的handler处理类。3、不止重写MybatisEnumTypeHandler&#xff0c;还重写CompositeEnumTypeHandler类3.1、修改Compos…
阅读更多...
【WPF】桌面程序开发之xaml页面主题和样式详解

【WPF】桌面程序开发之xaml页面主题和样式详解

使用Visual Studio开发工具&#xff0c;我们可以编写在Windows系统上运行的桌面应用程序。其中&#xff0c;WPF&#xff08;Windows Presentation Foundation&#xff09;项目是一种常见的选择。然而&#xff0c;对于初学者来说&#xff0c;WPF项目中xaml页面的布局设计可能是一…
阅读更多...
Bat的退役前

Bat的退役前

我们很讨厌bat 语法这版的命令形式后缀尽管古老&#xff0c;可是在涉及细微VS 项目op 时候&#xff0c;它起到了不可忽视且非它不行的效应 我们不想替历史背上厚重的学习包袱&#xff0c;可是我们能忽视BAT 吗 如若进入到 无window时代&#xff0c;我们几乎得全然依仗BAT专家。…
阅读更多...
35天学习小结

35天学习小结

距离上次纪念日&#xff0c;已经过去了35天咯 算算也有5周了&#xff0c;在这一个月里&#xff0c;收获的也挺多&#xff0c;在这个过程中认识的大佬也是越来越多了hh 学到的东西&#xff0c;其实也没有很多&#xff0c;这个暑假多多少少还是有遗憾的~ 第一周 学习了一些有…
阅读更多...
【计算机组成原理】详细解读带符号整数的原码表示法

【计算机组成原理】详细解读带符号整数的原码表示法

带符号整数的表示——原码 导读一、有符号整数的存储结构二、有符号整数的表现形式三、原码3.1 原码与真值之间的转换3.2 原码的运算3.3 原码的优缺点 结语 导读 大家好&#xff0c;很高兴又和大家见面啦&#xff01;&#xff01;&#xff01; 在上一篇内容中我们介绍了无符号…
阅读更多...
828华为云征文｜基于华为云Flexus云服务器X搭建jumpserver堡垒机软件

828华为云征文｜基于华为云Flexus云服务器X搭建jumpserver堡垒机软件

文章目录 ❀前言❀jumpserver堡垒机概述❀环境准备❀部署说明❀在线安装❀浏览器访问❀资产添加❀资产授权❀资产登录❀总结 ❀前言 近期华为云推出了最新的华为云Flexus云服务器X&#xff0c;这款云主机在算柔性算力做出了重大变革。华为云Flexus云服务器X基于擎天QingTian架…
阅读更多...
Xilinx FPGA 原语解析（二）：IBUFDS差分输入缓冲器（示例源码及仿真）

Xilinx FPGA 原语解析（二）：IBUFDS差分输入缓冲器（示例源码及仿真）

目录 前言&#xff1a; 一、原语使用说明 二、原语实例化代码模版 三、使用示例 1.设计文件代码 2.仿真文件代码 3.仿真结果 前言&#xff1a; 本文主要参考资料xilinx手册&#xff0c;《Xilinx 7 Series FPGA and Zynq-7000 All Programmable SoC Libraries Guide for…
阅读更多...
LeetCode 热题 100 回顾1

LeetCode 热题 100 回顾1

干货分享&#xff0c;感谢您的阅读&#xff01;原文见&#xff1a;LeetCode 热题 100 回顾_力code热题100-CSDN博客 一、哈希部分 1.两数之和 &#xff08;简单&#xff09; 题目描述 给定一个整数数组 nums 和一个整数目标值 target&#xff0c;请你在该数组中找出 和为目标…
阅读更多...
【Python 千题 —— 算法篇】词频统计

【Python 千题 —— 算法篇】词频统计

Python 千题持续更新中 …… 脑图地址 👉：⭐https://twilight-fanyi.gitee.io/mind-map/Python千题.html⭐ 题目背景 在日常开发和文本处理工作中，单词计数是一个非常基础但又极为重要的操作。无论是统计一篇文章的词频，还是分析一段文本的关键词，单词计数都起着关键作用…
阅读更多...
Spring Boot 集成 MinIO 与 KKFile 实现文件预览功能

Spring Boot 集成 MinIO 与 KKFile 实现文件预览功能

文件预览功能是提升用户体验的重要部分，尤其是在文档管理系统中。本文将带你逐步实现如何在 Spring Boot 项目中集成 MinIO（一个对象存储系统）与 KKFileView（一个开源文件预览工具），以实现对各种类型文件的在线预览 项目准备 Java 11+ Spring Boot MinIO 服务器 KKFileV…
阅读更多...
C语言 ——— 带副作用的宏参数

C语言 ——— 带副作用的宏参数

目录 带有副作用的代码 带有副作用的宏参数 结论 带有副作用的代码 代码演示&#xff1a; int a 10;int b a; 副作用解析&#xff1a; 变量 a 在赋值给 b 之前 a 的值自增了1&#xff0c;那么 int b a; 这条代码就带有副作用 带有副作用的宏参数 代码演示&#xff1a…
阅读更多...
学会收纳，对“衣服山”说再见，我推荐你读这4本书

学会收纳，对“衣服山”说再见，我推荐你读这4本书

面对日积月累形成的“衣服山”&#xff0c;我们还是会经常苦恼“没有衣服穿”&#xff0c;主要原因是我们出门前&#xff0c;很难用手边的衣服对相应的场合进行搭配。 我们的衣柜存在这样一个怪圈&#xff1a;衣柜里的衣服不断增加&#xff0c;尽管数量多&#xff0c;但是“能…
阅读更多...
CSS —— display属性

CSS —— display属性

用于指定一个元素在页面中的显示方式 HTML中标签元素大体被分为三种类型&#xff1a;块元素、行内元素和行内块元素 块元素 &#xff1a;block 1.独占一行 2.水平方向&#xff0c;占满它父元素的可用空间&#xff08;宽度是父级的100%&#xff09; 3.垂直方向&#xff0c;占据的…
阅读更多...
如何使用QT完成记事本程序的UI界面布局

如何使用QT完成记事本程序的UI界面布局

每日QT技巧查询表-CSDN博客 会持续更新记事本编写的全部过程&#xff0c;关注不迷路 一、相关控件 ①水平和垂直布局 ②按键 ③文本框 ④水平弹簧 ⑤标签 ⑥Widget 二、控件使用方法 1、PushButton 拖出三个按键&#xff0c;并对其进行命名&#xff0c;两处地方命名可以不一…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023