文章目录
- 树与二叉树的应用
- 1.哈夫曼树与哈夫曼曼编码
- 1.1 带权路径长度
- 1.2 哈夫曼树
- 1.2.1 哈夫曼树的构造
- 1.3 哈夫曼编码
- 2.并查集
- 2.1 并查集的三要素
- 2.1.1 并查集的逻辑结构
- 2.1.2 并查集的存储结构
- 2.2 并查集的优化
- 2.2.1 初步优化(并操作优化)
- 2.2.2 终极优化(查操作优化即压缩存储)
- 3.二叉排序树
- 3.1 二叉排序树的定义
- 3.2 二叉排序树的查找
- 3.3 二叉排序树的插入
- 3.4 二叉排序树的构造
- 3.5 二叉排序树的删除(重点)
- 3.6 查找效率分析(ASL)
- 4.平衡二叉树
- 4.1 平衡二叉树的定义
- 4.2 插入操作
- 4.3 插入新结点如何调整不平衡问题
- 4.4 查找效率分析
- 4.5 删除操作
树与二叉树的应用
文章目录:
1.哈夫曼树与哈夫曼曼编码
引入1.1:在学习哈夫曼树和哈夫曼编码之前预备知识
1.1 带权路径长度
结点的权:理解为权重,重要性。
结点的带权路径长度:树根到该结点的路径长度(经过的边数✖️该结点的权值)
树的带权路径长度(WPL):树中所有叶结点的带权路径长度之和。
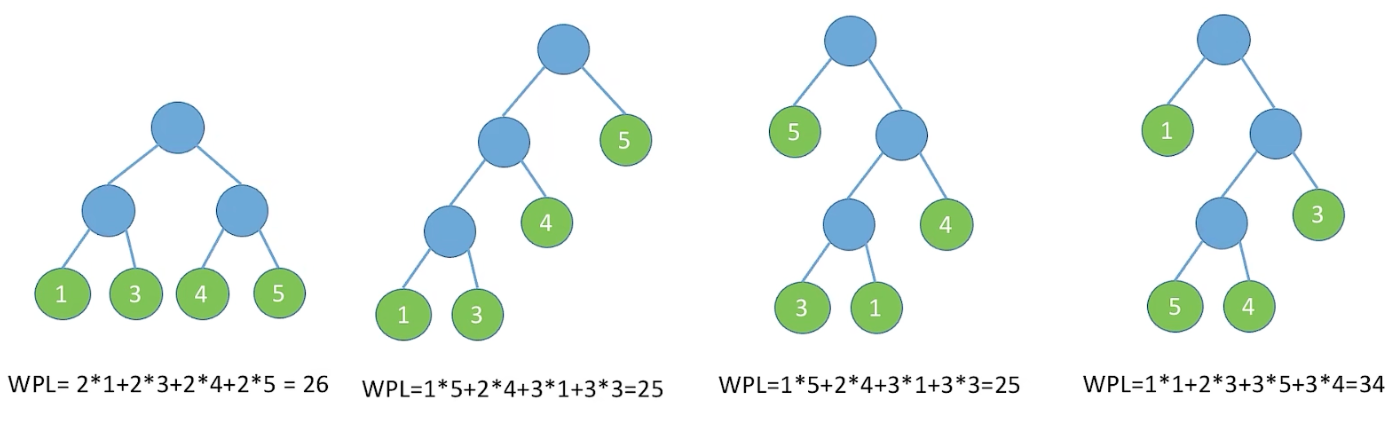
引入1.2 :在含有n个带权叶结点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称最优二叉树。
1.2 哈夫曼树
1.2.1 哈夫曼树的构造
构造步骤:
1️⃣ 找到当前权值最小的两个结点(包括两个结点构造出的新结点)
2️⃣ 将这两个结点通过一个构造出的父结点联系起来,父结点的权值是他俩权值之和。
3️⃣重复上面的步骤,直到没有结点可以添加
哈夫曼树特点:
- 每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大
- 哈夫曼树的结点总数为2n-1
- 哈夫曼树中不存在度为1的结点
- 哈夫曼树并不唯一,但WPL必然相同且为最优。
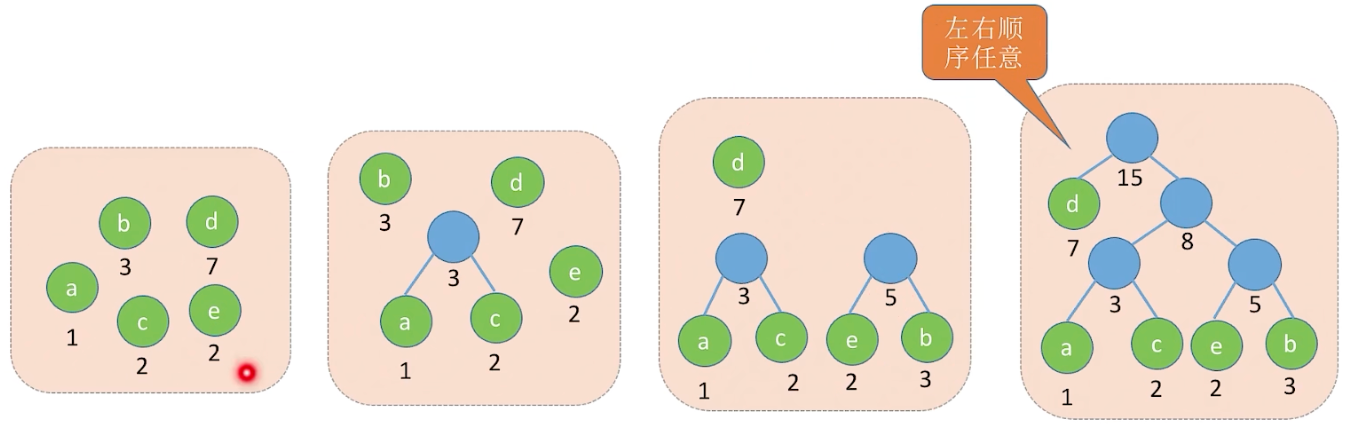
引入1.3 :哈夫曼树的应用->哈夫曼编码,简单理解成,把英文字母用最少的比特表达出来。常用的字母,访问的频率高,权值就高,尽可能的放在树层次低的位置,好进行查找。而构造哈夫曼树,就是用编码的字母配上上他们的权值,构造出一个哈夫曼树,然后做分支算0,右分支算1,将字母编码,不重不漏,且最优,访问时间最快。
1.3 哈夫曼编码
固定长度编码:每个字符用相等长度的二进制位表示
可变长度编码:允许对不同字符用不等长长的二进制位表示
前缀编码:若没有
一个编码是另一个编码的前缀,则称这样的编码为前缀编码。
特点:哈夫曼树不唯一,哈夫曼编码也不唯一,但是WPL是一样的
2.并查集
2.1 并查集的三要素
2.1.1 并查集的逻辑结构
并查集划分不同的集合。
将各种元素划分为若干互不相交的子集。
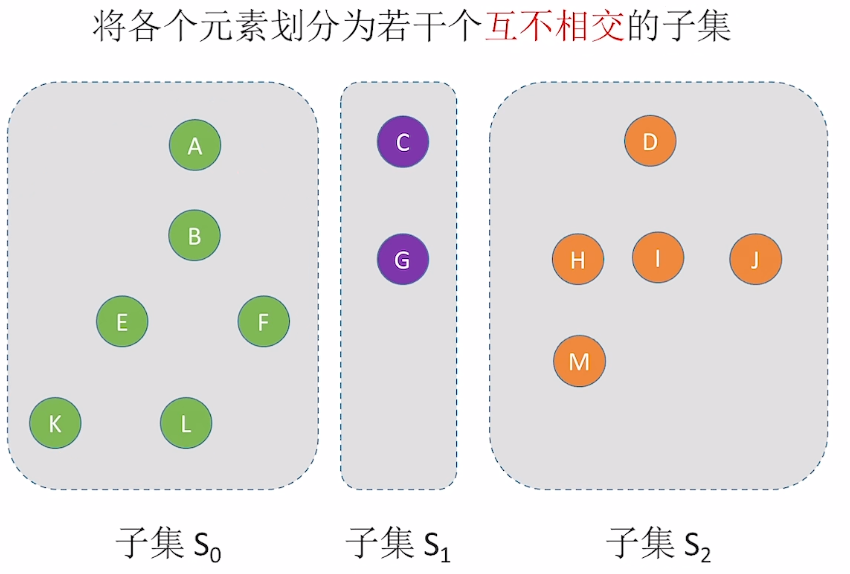
让这些子集组成一颗树,指向一个子集的根结点
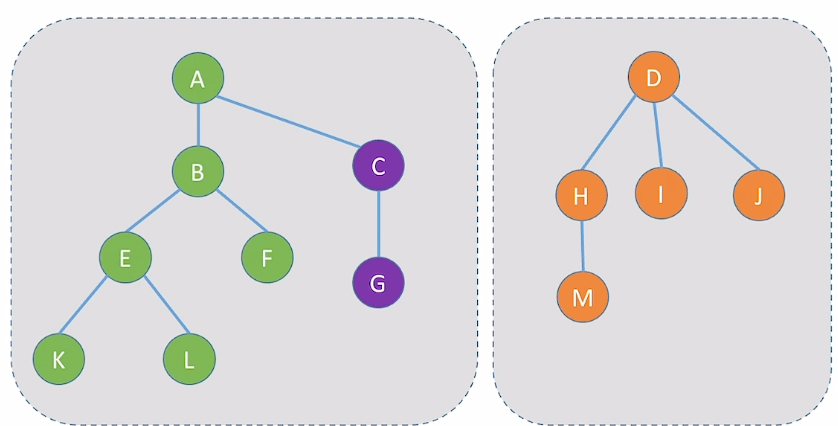
根据逻辑结构描述基本操作:
查:如查找两个结点,是否属于一个集合,两个结点分别查到对应集合树的根结点,并比较根结点是否相同
并:将一个子树的根结点,放到另一根子树根结点的下面,做它的孩子
2.1.2 并查集的存储结构
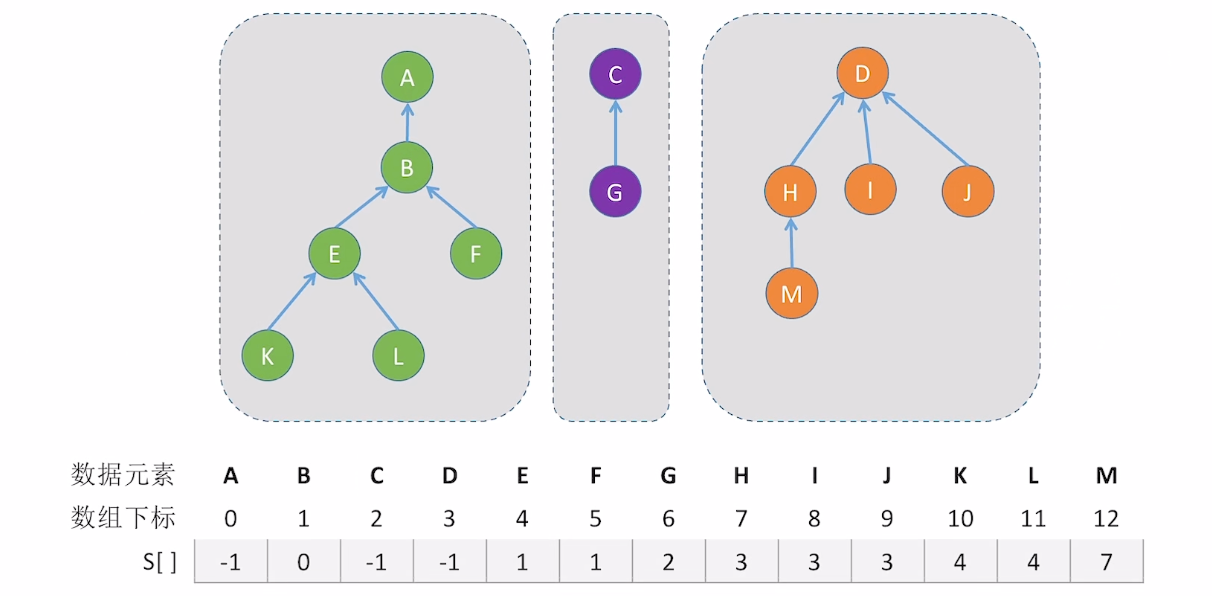
解释说明:
- 存储结构是静态数组,数组下标代表元素是哪个,数组中存储的值,代表它的父结点的下标是哪个,如果是-1,代表没有父结点,即就是根结点
- 注意,这个树的箭头,是由孩子指向双亲的
集合的两个操作:
查操作:从一个结点出发,一步一步找到根结点
并操作:将一个结点的存储值,改成合并的结点的下标。
2.2 并查集的优化
2.2.1 初步优化(并操作优化)
引入思考:
我们希望并查集的树是越宽越好,因为越深我们查找起来越慢,所以说,在并操作这个步骤,有可以改进的地方。我们应该确定两颗树,到底谁应该是谁的孩子,我们的核心目的是让更多的结点在树中的位置离根结点更近,所以,通过结点的个数确定两颗树的关系,结点少的做结点多的孩子,即小树合并到大树
存储结构的改变:
- 根结点存储的值不再是-1,而是根据他所构成的树所有的结点数确定这个值,如他有6个结点,根结点值就是-6,这样方便两个树比较结点数。
- 然后合并之后,把大树的值改成他俩原先的存储值之和,小树根存储值改为大树下标
2.2.2 终极优化(查操作优化即压缩存储)
引入思考:
我们希望并查集的树越宽越好,我们当然可以把某一段树放到根结点下面,降低他的深度,这个操作,我们在每次查找的过程中实现,即查找某一个点的根结点,然后再他包括他经过的所有结点放到根结点下方。
- 在这个过程中,修改途径结点的存储值,一步到位直接存储根结点的下标。
3.二叉排序树
3.1 二叉排序树的定义
二叉排序树,又称二叉查找树(BST)
一颗二叉树或者空二叉树,或者具有如下性质的二叉树:
- 左子树上所有结点的关键字均小于根结点的关键字
- 右子树上所有结点的关键字均大于根结点的关键字
- 左子树和右子树又各是一颗二叉排序树
3.2 二叉排序树的查找
从根结点出发,比根结点小走左子树,比根结点大走右子树,每次对比根结点,数值相等则查找成功,找到空子树则查找失败
3.3 二叉排序树的插入
若原二叉排序树为空,则直接插入结点,否则根据关键字先找插入位置,再进行插入操作,小的插在左边,大的插到右边
3.4 二叉排序树的构造
多次使用二叉排序树插入操作
注意:
- 不同的关键字可能得到同款二叉排序树
- 也可能得到不同款二叉排序树
3.5 二叉排序树的删除(重点)
二叉排序树根据删除结点的情况可分为三种情况:
先搜索找到目标结点:
1️⃣若被删除结点z是叶结点,则直接删除,不会破坏二叉排序树的性质。
2️⃣若被删除的结点只有左子树或右子树,直接让它的那个子树代替它的位置即可
3️⃣被删除的结点既有左子树又有右子树
- 从左子树找到最大的结点,代替它的位置(即左子树最右下的结点)
- 从右子树找到最小的结点,代替它的位置(即右子树最左下的结点)

3.6 查找效率分析(ASL)
查找长度:在查找运算中,需要对比关键字的次数称为查找长度,反映了查找操作时间的复杂度。
具体实例求查找成功的平均查找长度ASL
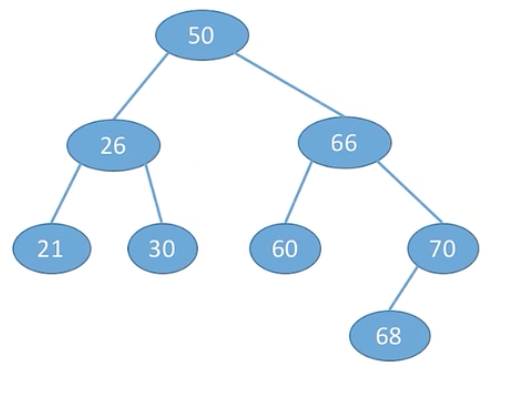
查找成功:
(查询次数✖️同等查询次数结点数)➗结点总数
ASL=(1*1+2*2+3*4+4*1)/8=2.625
具体实例求查找失败的平均查找长度ASL
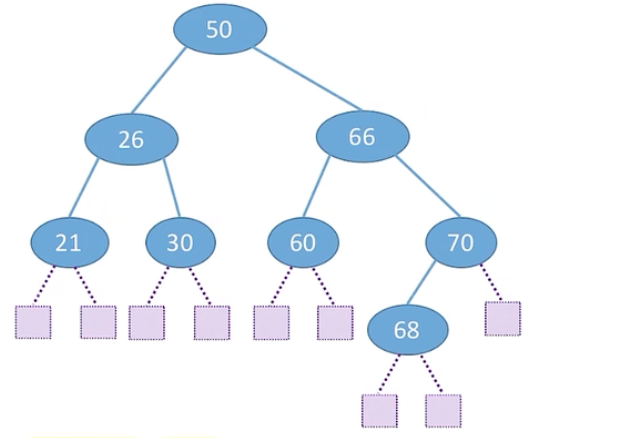
查找失败
(判断出是空子树需要的查找次数*这种情况的数量)/情况数
ASL=(3*7+4*2)/9=3.22
总结:
查找效率分析
最好情况:
n个结点的二叉树最小高度为⌊log2n⌋+1,平均查找长度=O(log2n)
最坏情况:
每个结点只有一个分支,树高h=结点n。平均查找长度O(n)
4.平衡二叉树
4.1 平衡二叉树的定义
平衡二叉树:简称AVL树,树上任一结点的左子树和右子树的高度之差不超过1
4.2 插入操作
在二叉排序树的插入操作中,不难得知,插入一个结点后,平衡二叉树可能就不平衡了,所以在每次插入完之后,我们就需要检查平衡二叉树,找出最小不平衡子树,然后调整最小不平衡子树。
4.3 插入新结点如何调整不平衡问题
根据插入位置不同,分为四种类型
- LL(插入在左孩子的左子树)
- RR(插入在右孩子的右子树)
- LR(插入在左孩子的右子树)
- RL(插入在右孩子的左子树)
为什么假定所有子树的高度都是H
如何调整最小不平衡子树?
记法:孩子反向旋转,左旋右旋指的是往上旋转
LL:左孩子右旋成为根结点,多出来的右子树,移动到原先根结点的左子树
RR:右孩子左旋成为根结点,多出来的左子树,移动到原先根结点的右子树
LR:右子树先左旋,再右旋
RL:左子树先右旋,再左旋
4.4 查找效率分析
我们以nh表示深度为h的平衡树中含有的最少结点数
不难推出:
n0=0
n1=1
n2=2
n3=4
总结归纳出,nh=nh-1+nh-2+1
可以证明n个结点的平衡二叉树的最大深度是O(log2n),平衡二叉树的平均查找长度为O(log2n)
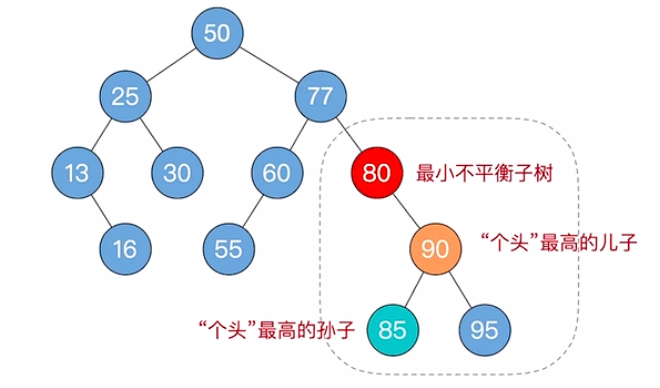
4.5 删除操作
1️⃣删除结点
若删除的结点是叶子,直接删
若删除的结点只有一个子树,用子树顶替删除位置
若删除的结点有两颗子树,用前驱(或后继结点)顶替,并转换为对前驱或后继结点的删除
2️⃣ 一路向上找到最小不平衡子树,若无则直接结束
3️⃣找最小不平衡子树下,"个头"最高的儿子和孙子
4️⃣根据孙子的位置,调整平衡(LL/RR/LR/RL)
5️⃣ 如果不平衡向上传导,继续2️⃣