前言
小时候听过一个小孩练琴的故事,老师让他先弹最简单的第一小节,小孩练了两天后弹不出。接着,老师让他直接去练更难的第二小节,小孩练习了几天后还是弹不出,开始感觉到挫败和烦躁了。
小孩以为老师之后会让他从简单的开始练,谁知老师直接让他开始练最难的一小节。小孩不干了,问老师是不是故意刁难他。
老师笑笑,让他现在弹弹第一小节试试。神奇的是,小孩竟然发现自己已经能完整弹出来了。
这有点像我现在的学习状况,前些天我还没搞明白线性模型和多层感知机,就去看了后面卷积神经网络的内容。现在再回看前面的内容时,竟然发现有点豁然开朗了,所以有了前一篇文章。
当然并不是学任何东西都可以像练琴故事里那样,往后学着学着,前面的自然就会了。
我想说的其实是,不要老想着有什么很好的学习方法,陷入“完美主义”而迟迟不开始学。
学就是了,或许学着学着,你就可以搞明白之前觉得困惑的地方。
当然,也不能非常头铁,也是需要一定的“顶层设计”的。学的过程中要时刻搞清楚“是什么”和“为什么”。
一、softmax 回归
前面我们学习了回归,它可以帮助我们解决“多少”的问题。比如预测房屋的价格是多少,某支篮球队的胜场数是多少等等。
在生活中,我们除了会碰到“多少”的问题,还会碰到“哪一个”的分类问题,如:
- 某个图像是蚂蚁还是蜜蜂?
- 某人有可能去看哪一部电影?
这两个的问题界限比较模糊,其中一个原因是分类可以用回归实现。
就比如,我们只希望得到结果到底是哪个类别,到底是蚂蚁还是蜜蜂。
但在实现时,我们会采用连续值的方法,即如果这张图片属于蚂蚁的概率超过了某个值,我们就把它分为蚂蚁这一类。
分类问题
我们从一个图像分类问题开始。假设每次输入的是一个 2 × 2 2\times2 2×2 的灰度图像,需要判断其是“猫”、“狗”还是“鸡”。
对图像的基本知识不清楚的,可以另外看看其他资料。
我们可以用一个标量表示每个像素值,这样一个图像就对应于四个特征 x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4。
接下来,我们要选择如何表示类别(标签)。统计学家发明了一种简单的表示分类数据的方法:独热编码(one-hot encoding)。
独热编码是一个向量,它的分量和类别一样多。类别对应的分量设为 1,其他分量设为 0。
网络架构
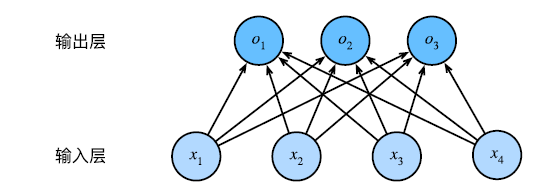
前面提到,我们实现分类需要计算出所有可能类别的条件概率,因此需要一个有多输出的模型,每个类型对应于一个输出。
为了解决线性模型的分类问题,我们需要和输出一样多的仿射函数(affine function),每个输出对应于它自己的仿射函数。
与线性回归一样,softman 回归也是一个单层神经网络(如下图)。由于计算每个输出取决于所有输入,所以 softmax 回归的输出层也是全连接层。
softmax 运算
有了多个输出后,怎么确定好分类结果呢?我们设置一个阈值,比如选择具有最大概率的标签作为预测类别。
例如,得到的三个输出分别为 0.8,0.1 和 0.1,那么我们预测的类别可以说是 1。
若是出现三个输出为 0.8,0.6 和 0.4 呢?我们还能直接确定预测类别是 1 吗?
答案是否定的。一方面,线性层没法保证所有输出之和为 1;另一方面,不同的输入,输出结果可能是负值。这两条违反了概率的基本公理。
要将输出视为概率,我们必须保证在任何数据上的输出是非负的且总和为 1。此外,我们需要一个训练的目标函数,来激励模型精准地估计概率。
例如,在分类器输出 0.5 的所有样本中,我们希望这些样本确实是有一半预测对了。这个属性称为校准(calibration)。
1959 年,社会科学家邓肯·卢斯在选择模型(choice model)的基础上,发明的 s o f t m a x softmax softmax 函数正是这样做的:
softmax 函数能够将未规范化的预测变换为非负数且总和为 1,同时让模型保持可导的性质。如下式:
y
^
=
s
o
f
t
m
a
x
(
o
)
,
y
^
j
=
exp
o
j
∑
k
exp
(
o
k
)
\hat{\pmb{y}}=softmax(\pmb{o}),\hat{y}_j=\frac{\exp{o_j}}{\sum_k\exp{(o_k)}}
y^=softmax(o),y^j=∑kexp(ok)expoj
这个让我想起了交通规划里的 Logit 模型,也是通过这个公式将效用转为选择概率的。
尽管 softmax 是一个非线性函数,但 softmax 回归的输出仍然是由输入特征的仿射变换决定的。因此,softmax 回归是一个线性模型(linear model)。
二、softmax 回归的从零开始实现
准备数据集
与线性回归实现时我们自己生成数据集不同,我们借助已有的图像分类数据集 Fashion-MNIST。
Fashion-MNIST由10个类别的图像组成,分别为t-shirt(T恤)、trouser(裤子)、pullover(套衫)、dress(连衣裙)、coat(外套)、sandal(凉鞋)、shirt(衬衫)、sneaker(运动鞋)、bag(包)和ankle boot(短靴)。
每个类别由训练数据集(train dataset)中的6000张图像和测试数据集(test dataset)中的1000张图像组成。
因此,训练集和测试集分别包含60000和10000张图像,图像大小为 28 × 28 28\times28 28×28。测试数据集不会用于训练,只用于评估模型性能。
torchvision 为我们提供了一系列机器视觉工具包,其中就包括图像数据集及图像处理工具 transforms。
为了使我们读取图像时更轻松,我们直接使用 DataLoader,并使用多线程 loader_num 读取数据集。
将下载数据集与读取数据集整合进一个函数中,并加入 resize 参数用于对图像大小进行调整。
def load_data_fashion_mnist(batch_size, loader_num, resize=None): # 数据集准备
"""下载Fashion-MNIST数据集,然后将其加载到内存中"""
trans = [transforms.ToTensor()] # 数据变换操作列表
if resize: # 如果需要改变形状的话,把resize的操作加到变换列表里
trans.insert(0, transforms.Resize(resize))
trans = transforms.Compose(trans) # 将变换操作集合起来
# 下载训练集和数据集
mnist_train = torchvision.datasets.FashionMNIST(
root="../dataset", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
root="../dataset", train=False, transform=trans, download=True)
return (data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=loader_num),
data.DataLoader(mnist_test, batch_size, shuffle=False,
num_workers=loader_num))
这段代码的逻辑是:首先创建一个只有改变数据格式操作的列表,接着判断是否需要改变图像形状大小,如果需要,则将其加入到列表中。
接着下载 torchvision 中的训练/测试集,最后函数返回两个 DataLoader,分别用于读取训练和测试集。
初始化模型参数
对于 28 × 28 28\times28 28×28 的图像,如果我们把每个像素位置看作一个特征的话,其具有 28 × 28 = 784 28\times28=784 28×28=784 个特征,因此模型的输入为 784 维。数据集具有 10 个类别,故输出维度为 10。
softmax 回归也可视为线性模型,因此其同样只具有两个参数:权重
w
w
w 和偏置
b
b
b。其中权重为
784
×
10
784\times10
784×10 的矩阵,偏置为
1
×
10
1\times10
1×10 行的向量,即
y
1
×
10
=
x
1
×
784
w
784
×
10
+
b
1
×
10
\pmb{y}_{1\times10}=\pmb{x}_{1\times784}\pmb{w}_{784\times10}+b_{1\times10}
y1×10=x1×784w784×10+b1×10
权重采用均值为 0,标准差为 0.01 的正态分布随机数初始化,偏置初始设置零向量。
num_inputs = 784
num_outputs = 10
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)
定义 softmax 操作
因为模型中需要通过 softmax 运算将输出的结果转为概率,因此在定义模型前需要先定义 softmax 操作。
softmax 操作由以下三个步骤组成:
- 对每项求 exp 幂;
- 对每一行求和(每一行代表一个样本),得到每个样本的规范化常数;
- 每一行除以其规范化常数,确保结果之和为 1。
def softmax(X): # 定义 softmax 操作
X_exp = torch.exp(X)
partition = X_exp.sum(1, keepdim=True) # keepdim 指保持维度不变
return X_exp / partition # 这里应用了广播机制
定义模型
定义好 softmax 操作后,我们就可以定义 softmax 回归模型。
这里注意需要对输入的 X 进行 reshape 操作,将其展平为 1 × 784 1\times784 1×784。
def net(X): # 定义模型
return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)
定义损失函数
与线性回归采用平方损失函数不同,softmax 回归采用的是交叉熵损失(cross-entropy loss)。
对于任何标签
y
\pmb{y}
y 和模型预测
y
^
\hat{\pmb{y}}
y^,损失函数为:
l
(
y
,
y
^
)
=
−
∑
j
=
1
q
y
j
log
y
^
j
.
l(\pmb{y},\hat{\pmb{y}})=-\sum_{j=1}^qy_j\log{\hat{y}_j}.
l(y,y^)=−j=1∑qyjlogy^j.
这可能是深度学习中最常见的损失函数,因为分类问题的数量远远超过回归问题的数量。
def cross_entropy(y_hat, y): # 交叉熵损失函数
return - torch.log(y_hat[range(len(y_hat)), y])
定义优化器
我们仍然采用小批量随机梯度下降对参数进行更新,代码和前面线性回归的一样。
def my_optimizer(params, lr, batch_size): # 定义优化器
"""小批量随机梯度下降"""
with torch.no_grad(): # 以下操作不计算梯度
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
分类精度
给定预测概率 y ^ \hat{y} y^,当我们必须输出硬预测(hard prediction)时,我们通常选择预测概率最高的类。
当预测与真实标签一致时,说明该样本预测正确。分类精度即预测正确的样本数与总样本数之比。
精度是我们最关心的性能衡量标准,几乎所有分类问题都会关注它。
我们首先定义一个计算精度的函数,当传入预测值和真实值时,这个函数可以返回预测正确的数量。
def accuracy(y_hat, y):
"""计算预测正确的数量"""
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = y_hat.argmax(axis=1)
cmp = y_hat.type(y.dtype) == y
return float(cmp.type(y.dtype).sum())
当模型训练完后,我们还需要计算其在测试集上的表现,因此我们可以定义一个函数,用于计算模型在指定数据集上的精度。
def evaluate_accuracy(net, data_iter):
"""计算在指定数据集上模型的精度"""
if isinstance(net, torch.nn.Module):
net.eval() # 将模型设置为评估模式
metric = Accumulator(2) # 正确预测数、预测总数
with torch.no_grad():
for X, y in data_iter:
metric.add(accuracy(net(X), y), y.numel())
return metric[0] / metric[1]
由于是小批量读取,我们还需要定义一个累加器 Accumulator 类,用于得到整个数据集的精度。
class Accumulator:
"""在n个变量上累加"""
def __init__(self, n):
self.data = [0.0] * n
def add(self, *args):
self.data = [a + float(b) for a, b in zip(self.data, args)]
def reset(self):
self.data = [0.0] * len(self.data)
def __getitem__(self, idx):
return self.data[idx]
训练
softmax 回归的训练过程和线性回归很类似,从初始的参数出发,逐轮训练计算损失并更新。
因为我们需要查看每一轮训练后的效果,所以需要单独定义一个训练一轮的函数。
除此之外,我们还需要定义一个完整训练的函数,该函数反复调用训练一轮的函数。这样当换了一个模型时,我们也只需要改变传入的参数即可实现新模型的训练。
训练一轮的函数代码如下。函数内首先判断这个模型是否是实例化了 nn.Module 这个类,例如线性回归从零开始的模型是自己实现的,而简洁实现则是使用了 nn.Linear。
之后定义累加器,开始 for 循环批量读取训练集,计算损失并更新。接着,判断是调用了 pytorch 的损失函数和优化器,还是使用了自己写的,各自有不同的写法。
最后返回整个训练集的平均训练损失与训练集上的精度。
def train_epoch(net, train_iter, loss, updater): #@save
"""训练模型一个迭代周期"""
# 将模型设置为训练模式
if isinstance(net, torch.nn.Module):
net.train()
# 训练损失总和、训练准确度总和、样本数
metric = Accumulator(3)
for X, y in train_iter:
# 计算梯度并更新参数
y_hat = net(X)
l = loss(y_hat, y)
if isinstance(updater, torch.optim.Optimizer):
# 使用PyTorch内置的优化器和损失函数
updater.zero_grad()
l.mean().backward()
updater.step()
else:
# 使用定制的优化器和损失函数
l.sum().backward()
updater([W, b], lr, batch_size)
metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
# 返回训练损失和训练精度
return metric[0] / metric[2], metric[1] / metric[2]
完整训练的函数代码如下。在传入模型、训练集、测试集、损失函数、训练轮数和优化器后,进入 for 循环,开始调用训练一轮的函数,可以返回该轮训练后的损失以及精度。
接着利用 evaluate_accuracy 函数计算此轮训练后的模型在测试集上的精度。往后的 writer 和 print 都是为了可视化训练情况,其中前者是利用了 pytorch 自带的 tensorboard。
def train(net, train_iter, test_iter, loss, num_epochs, updater):
"""训练模型"""
for epoch in range(num_epochs):
train_loss, train_acc = train_epoch(net, train_iter, loss, updater)
test_acc = evaluate_accuracy(net, test_iter)
writer.add_scalar('train_loss', train_loss, epoch)
writer.add_scalar('train_acc', train_acc, epoch)
writer.add_scalar('test_loss', test_acc, epoch)
print(f'第{epoch + 1}轮的训练损失为{train_loss}')
print(f'第{epoch + 1}轮的训练精度为{train_acc}')
print(f'第{epoch + 1}轮的测试集精度为{test_acc}')
return train_loss, train_acc, test_acc
以上是实现模型训练所需要的函数,下面我们开始编写主代码。李沐老师的代码是用 jupyter notebook 编写的,而我是用 pycharm,有些时候就会报错。
我猜测可能是设置了多线程的原因,我需要把主代码写在 if __name__ == '__main__': 里才可以运行。
if __name__ == '__main__':
lr = 0.1 # 学习率
batch_size = 256
writer = SummaryWriter('./runs') # 设置tb文件保存位置
train_iter, test_iter = load_data_fashion_mnist(batch_size, 4)
# 初始化权重和偏置
num_inputs = 784
num_outputs = 10
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)
# 设置随机种子,方便复现
random_seed = 326
torch.manual_seed(random_seed)
# 训练
num_epochs = 40
train_loss, train_acc, test_acc = train(net, train_iter, test_iter, cross_entropy, num_epochs, my_optimizer)
writer.close()
开始运行后,训练过程的数据会被记录在 ./runs 文件夹下,即当前目录下的 runs 文件夹下。
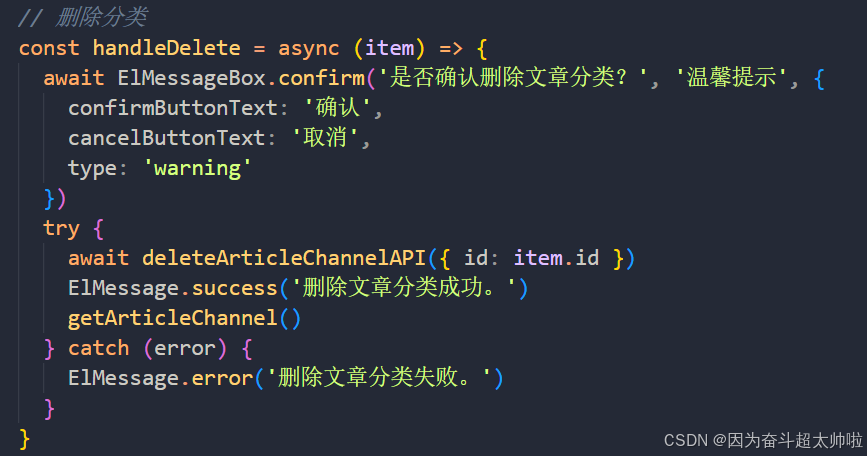
我们在左侧目录下找到 runs 文件夹,右键选择复制相对路径。接着打开底部 Terminal,输入 conda activate pytorch 激活项目的虚拟环境,回车。
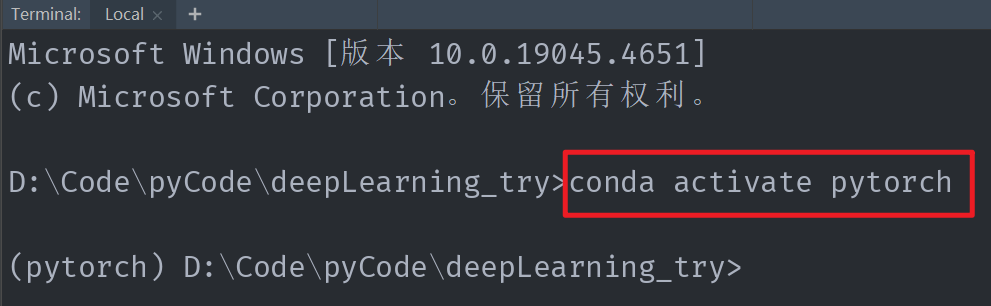
配置 pytorch 环境我是按照 b 站土堆视频来的,环境名称就叫 pytorch。
随后,输入 tensorboard --logdir=,接着粘贴刚复制的相对路径,回车,它会返回给你一个网址,点击它即可进入 tensorboard。
随后点击上方右侧的 SCALARS,就可以看到我们本次训练的训练损失、训练精度、测试精度随训练轮数的变化。
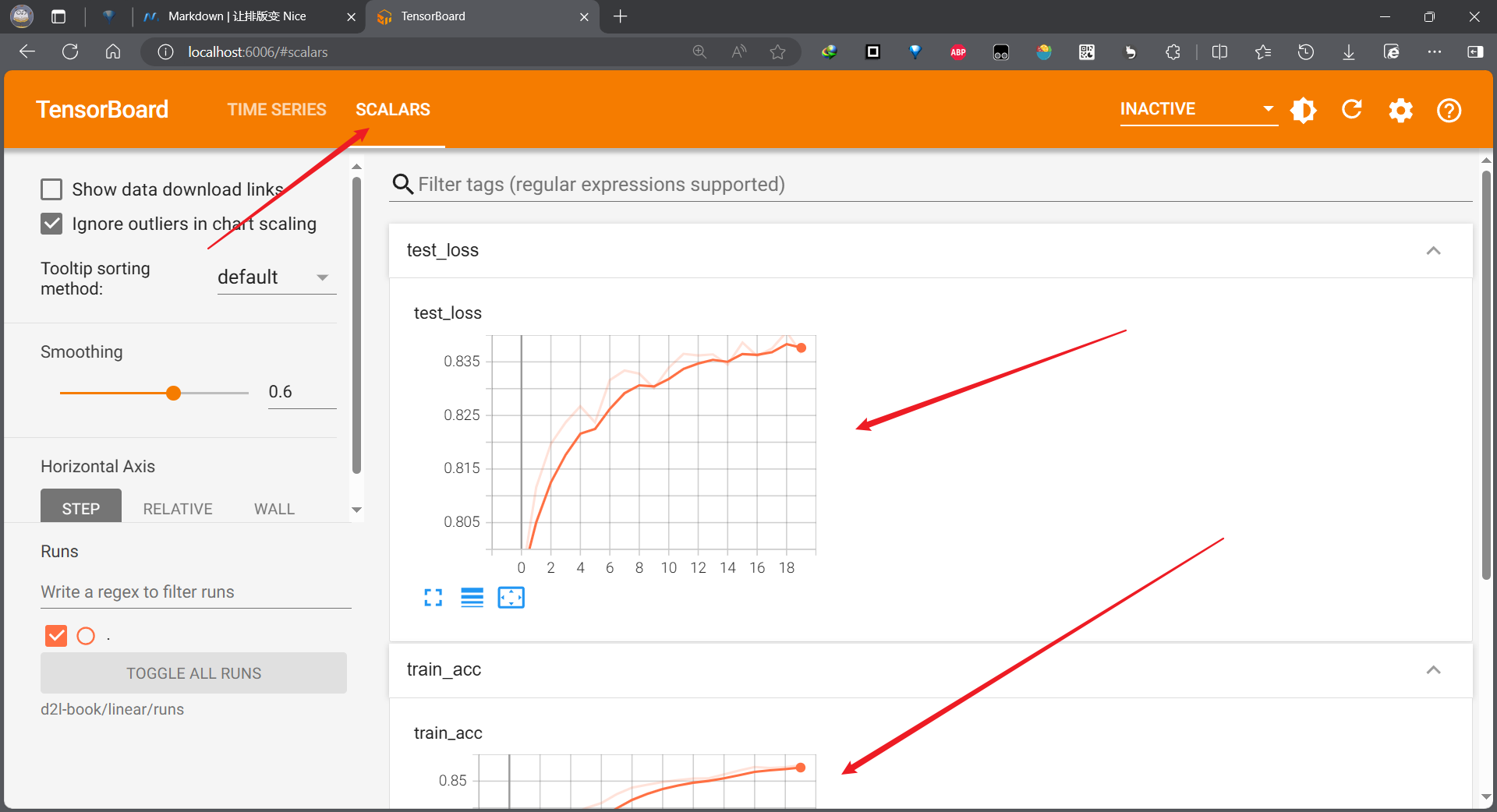
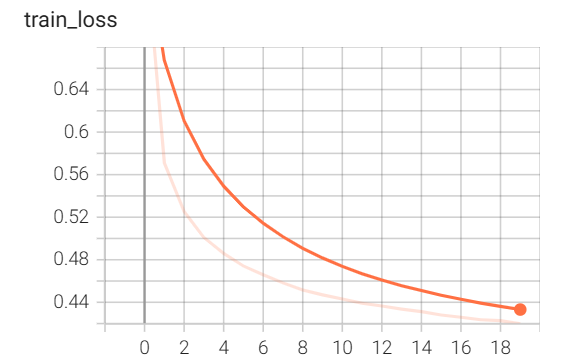
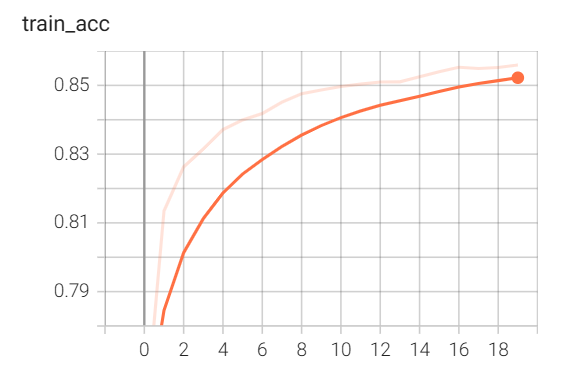
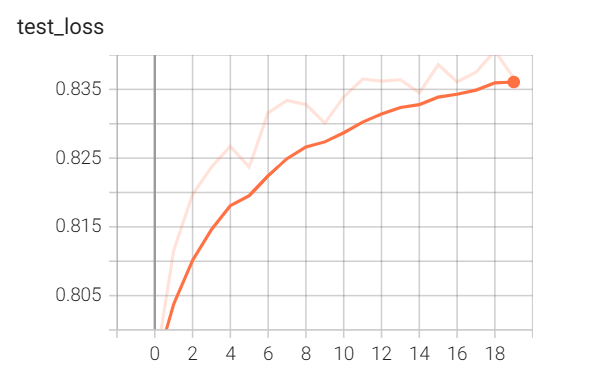
从图中可以发现,训练损失并未收敛到一个稳定的常数,其他两项也是。不过要注意纵坐标,训练精度和测试精度其实已经算比较稳定了。
另外,运行的时间也比较长,因此,我打算增加训练轮数到 40 轮,并利用 GPU 进行训练。
增加训练轮数简单,把 num_epochs 改为 40 即可。
利用 GPU 训练的话,需要数据、模型都放进 GPU。定义的使用 GPU 的函数如下:
def try_gpu(i=0): # 有 GPU 则使用,否则使用 CPU
"""如果存在,则返回gpu(i),否则返回cpu()"""
if torch.cuda.device_count() >= i + 1:
return torch.device(f'cuda:{i}')
return torch.device('cpu')
接着在相应模型和数据后添加 .to(try_gpu()),具体位置可见文章末尾完整代码,我是按照土堆视频里那样加的。
再次运行前,记得把原本 runs 文件夹下的文件先删掉,不然可能出来的图中含有上一次的数据。
运行过程中我看着控制台,似乎打印的速度和前面用 CPU 差不多,我还上网搜了怎么确认使用了 GPU 训练。
打开任务管理器和使用 nvidia-smi 都显示 GPU 在使用。同时我注意到我的 CPU 使用率是 100%。
网上说是可能还存在读写操作,所以影响 GPU 的使用,我感觉可能是 tensorboard 的使用导致的。不管了,我也忘了测一下运行时间,后面再研究研究。
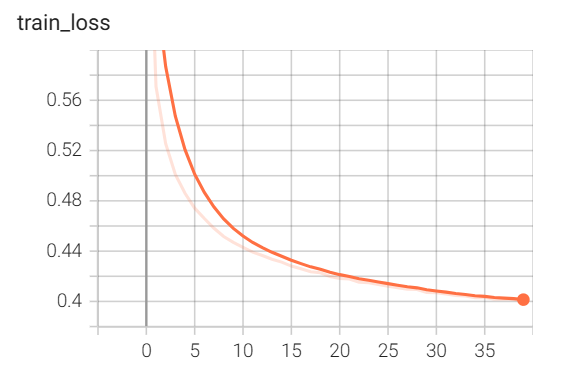
训练了 40 轮后的相关结果如下,感觉不错。
第40轮的训练损失为0.4002220250447591
第40轮的训练精度为0.86335
第40轮的测试集精度为0.8424
遗憾地是,从训练损失变化图来看,40 轮训练似乎也并未收敛。
三、softmax 回归的简洁实现
下面我们使用 pytorch 框架来简洁地实现 softmax 回归。准备数据集和前面一样,用的同一个函数,batch_size 也不变。
定义模型与初始化模型参数
回想一下从零开始实现,原本数据集中的图像大小是
28
×
28
28\times28
28×28,我们把它 reshape 成
1
×
784
1\times784
1×784 才传入线性层。这一操作称为展平,pytorch 中有专门的层(Flatten())来实现类似的处理。
因此,softmax 使用的模型有两层,一层为 Flatten(),另一层为 nn.Linear(784, 10)。
# PyTorch不会隐式地调整输入的形状。因此,
# 我们在线性层前定义了展平层(flatten),来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10)) # 定义模型
在简洁实现线性回归时,由于其只有一层线性层,初始化模型采用的是直接指定net[0]的两个参数。
而如果层数较多时,直接指定不太方面,我们可以自己定义一个权重的函数,利用 net.apply 对每一层进行初始化,而如果需要对某层进行特定操作时,可在函数中加入 if 判断。
def init_weights(m): # 对特定层的权重进行初始化,偏置默认为0初始化
if type(m) == nn.Linear:
nn.init.normal_(m.weight, mean=0, std=0.01)
损失函数
损失函数直接调用 nn 模块下的现成函数即可。
loss = nn.CrossEntropyLoss(reduction='none') # 损失函数,这里取值none即直接返回loss向量
优化器
优化器通用,调用 nn.optim 下现成的函数即可。
optimizer = torch.optim.SGD(net.parameters(), lr=lr) # 优化器
训练
进行训练可以直接调用我们在从零开始实现时写好的训练函数。由于我们在训练函数中已经进行了if判断,因此只要直接修改传入的参数即可。
num_epochs = 10
train_loss, train_acc, test_acc = train(net, train_iter, test_iter, loss, num_epochs, optimizer)
运行如下程序可得到第十轮训练后的相关评估结果。
if __name__ == '__main__':
lr = 0.1 # 学习率
batch_size = 256
writer = SummaryWriter('./runs/softmax_concise') # 设置tb文件保存位置
train_iter, test_iter = load_data_fashion_mnist(batch_size, 4)
# 初始化权重和偏置(简洁实现时未采用)
num_inputs = 784
num_outputs = 10
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs),
requires_grad=True, device=try_gpu())
b = torch.zeros(num_outputs, requires_grad=True, device=try_gpu())
# 设置随机种子,方便复现
random_seed = 326
torch.manual_seed(random_seed)
# PyTorch不会隐式地调整输入的形状。因此,
# 我们在线性层前定义了展平层(flatten),来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10)) # 定义模型
net = net.to(try_gpu())
net.apply(init_weights) # 初始化模型参数
loss = nn.CrossEntropyLoss(reduction='none') # 损失函数,这里取值none即直接返回loss向量
optimizer = torch.optim.SGD(net.parameters(), lr=lr) # 优化器
num_epochs = 10
train_loss, train_acc, test_acc = train(net, train_iter, test_iter, loss, num_epochs, optimizer)
writer.close()
第10轮的训练损失为0.4472448839187622
第10轮的训练精度为0.8485666666666667
第10轮的测试集精度为0.8322
softmax 回归的两种实现代码见附件:















![[PS]Photoshop 2024下载安装教程附软件包百度网盘分享链接地址](https://i-blog.csdnimg.cn/direct/76128aaa92fe4e259dd5d53f535827a8.png)