矩阵（加速）。。。

news2024/12/28 2:18:54

我限定你在明天中午之前搞定这东西！毕竟之前做过了欸。矩阵，一个看起来很神奇的东西，不过我不打算花太多的时间做这个，还是图论和数论好点儿，还要复习一下之前的数据结构和dp呢。那么先谈谈定义，定义一个矩阵就是一堆数，按照矩形排列形成的集合，那么加法的话用处不大，我们单学乘法，乘法，感觉得先搞懂定义：放一下别人的说法？
在这里插入图片描述
理解一下啊，就是先横后竖，若是不够形象那你可以将一个矩阵转个90度再对比？其实说的也不是这个，这个定义看看就好，重要的是其的的用处。第一当然是可以维护类斐波拉契数列的式子啦，第二也可以用于维护图，第三？动态dp吧好像，不过我还没学。
还有一个问题，就是单位矩阵！这个挺重要的，对于大部分快速幂来说都需要一个单位矩阵，有人用1，有人我不说。再看看那个大佬的在这里插入图片描述
P3390 【模板】矩阵快速幂重新写了一份。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,mod=1e9+7;
struct node 
{
	int n,m,w[220][220];
};node aa,bb;
void init(node &now,int x)
{
	now.n=x,now.m=x;memset(now.w,0,sizeof(now.w));
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
void clean(node &now)
{
	memset(now.w,0,sizeof(now.w));
	return ;
}
node operator * (const node &a,const node &b)
{
	node rt;rt.n=a.n,rt.m=b.m;clean(rt);
	if(a.m!=b.n) return rt;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			for(int k=1;k<=n;k++) rt.w[i][j]=(rt.w[i][j]+a.w[i][k]*b.w[k][j]%mod)%mod;
		}
	}
	return rt;
};
signed main()
{
	int k;scanf("%lld%lld",&n,&k);aa.n=n,aa.m=n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++) scanf("%lld",&aa.w[i][j]);
	}
	node ans;init(ans,n);
	while(k)
	{
		if(k%2==1) ans=(ans*aa);
		aa=aa*aa; k>>=1;	
	}
	for(int i=1;i<=ans.n;i++)
	{
		for(int j=1;j<=ans.m;j++) printf("%lld ",ans.w[i][j]%mod);
		printf("\n");
	}
	return 0;
}

P6435 「EZEC-1」数列很细节的操作呢，对于这个序列前移操作确实没想到。
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
int n,s,m,k;
struct node
{
	int n,m,w[101][101];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{
				for(int k=1;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+x.w[i][k]*y.w[k][j]);
			} 
		}
		return rt;
	};
};node ans;
void init(node &now,int x)
{
	now.n=x,now.m=x;
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
node ksm(node x,int k)
{
	node base;init(base,n); 
	while(k)
	{
		if(k&1) base=base*x;
		x=x*x;k>>=1;
	}
	return base;
}
int main()
{
	scanf("%d%d%d%d",&n,&s,&m,&k);node x;ans.n=ans.m=n;x.n=x.m=n;
	for(int i=1;i<=n;i++) scanf("%d",&ans.w[1][i]);
	for(int i=1;i<=n;i++) x.w[1+i%n][i]=1;
	swap(x.w[s],x.w[m]);ans=ans*ksm(x,k);
	for(int i=1;i<=n;i++) printf("%d ",ans.w[1][i]);
	return 0;
}

P2044 [NOI2012] 随机数生成器这个矩阵是我自己手推的！（虽然不是很难）但还是很厉害！

#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,k,a,c,mod,g;
int gsc(int x,int y)
{
	int rt=0;(x+=mod)%mod;(y+=mod)%mod;
	while(y)
	{
		if(y&1) rt=(rt+x)%mod;
		x=(x+x)%mod;y>>=1;
	}
	return rt;
}
struct node
{
	int n,m,w[201][201];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{	
				for(int k=1;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+gsc(x.w[i][k]%mod,y.w[k][j]%mod)+mod)%mod;
			}
		}
		return rt;
	}
};node ans;
void init(node &now,int x)
{
	now.m=now.n=x;	
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
node ksm(node x,int k)
{ 
	node rt;init(rt,2);
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1;
	}
	return rt;
}
signed main()
{
	scanf("%lld%lld%lld%lld%lld%lld",&mod,&a,&ans.w[1][2],&ans.w[1][1],&k,&g);
	node x;x.n=x.m=2;x.w[1][1]=a;x.w[2][1]=x.w[2][2]=1;ans.n=ans.m=2;
	ans=ans*ksm(x,k);printf("%lld",(g+ans.w[1][1])%g);
	return 0;
}

P3216 [HNOI2011]数学作业说句闲话，学习数学的最好方式就是：睡大觉。那么不妨尝试推一推每一位的式子在这里插入图片描述

#include<bits/stdc++.h>
#define int long long 
using namespace std;
int n,m,mod,t[100001];
struct node 
{
	int n,m,w[101][101];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{
				for(int k=1;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+x.w[i][k]%mod*y.w[k][j]%mod)%mod;//printf("%lld\n",rt.w[i][k]);
			}
		}
		return rt;
	}; 
};node ans,c;
void init(node &now,int x)
{
	now.n=now.m=x;memset(now.w,0,sizeof(now.w));
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
node power(node x,int k)
{
	node rt;init(rt,3);
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1;
	}
	return rt;
}
signed main()
{
	scanf("%lld%lld",&n,&mod);ans.n=ans.m=c.n=c.m=3;t[0]=1;
	ans.w[1][2]=ans.w[1][3]=c.w[2][1]=c.w[2][2]=c.w[3][2]=c.w[3][3]=1;
	for(int i=1;i<=19;i++) t[i]=t[i-1]*10;
	for(int i=1;i;i++)
	{
		c.w[1][1]=t[i]%mod;int tmp=min(n,t[i]-1)-t[i-1]+1;
		ans=ans*power(c,tmp);if(t[i]-1>=n) break;
	}
	printf("%lld",ans.w[1][1]);
	return 0;
}

P1397 [NOI2013] 矩阵游戏呃这个要用费马小定理的散了吧。
那么学一学图论版？P2151 [SDOI2009] HH去散步，大概我会努力说明白的吧，欸，你有没有认真理解过矩阵的性质，你真的知道(a*b=c)的c数组如何得出来的嘛？不会的话快去看看别人的题解（https://www.luogu.com.cn/problem/solution/P2151）学一学哈哈哈哈哈。
既然你已经对矩阵的本质有了些基础的了解，不妨想一想，a矩的第一行，与b矩的第一列，与c第一个点的关系？显然，乘积和对吧，感性的看看，那么仔细一想，好像有点想法，是什么呢，不妨设f[i][j]是从i到j的路径数吧，然后你想想，它每一行枚举的是什么。形象而言f[3][1]对吧，你要走一转。
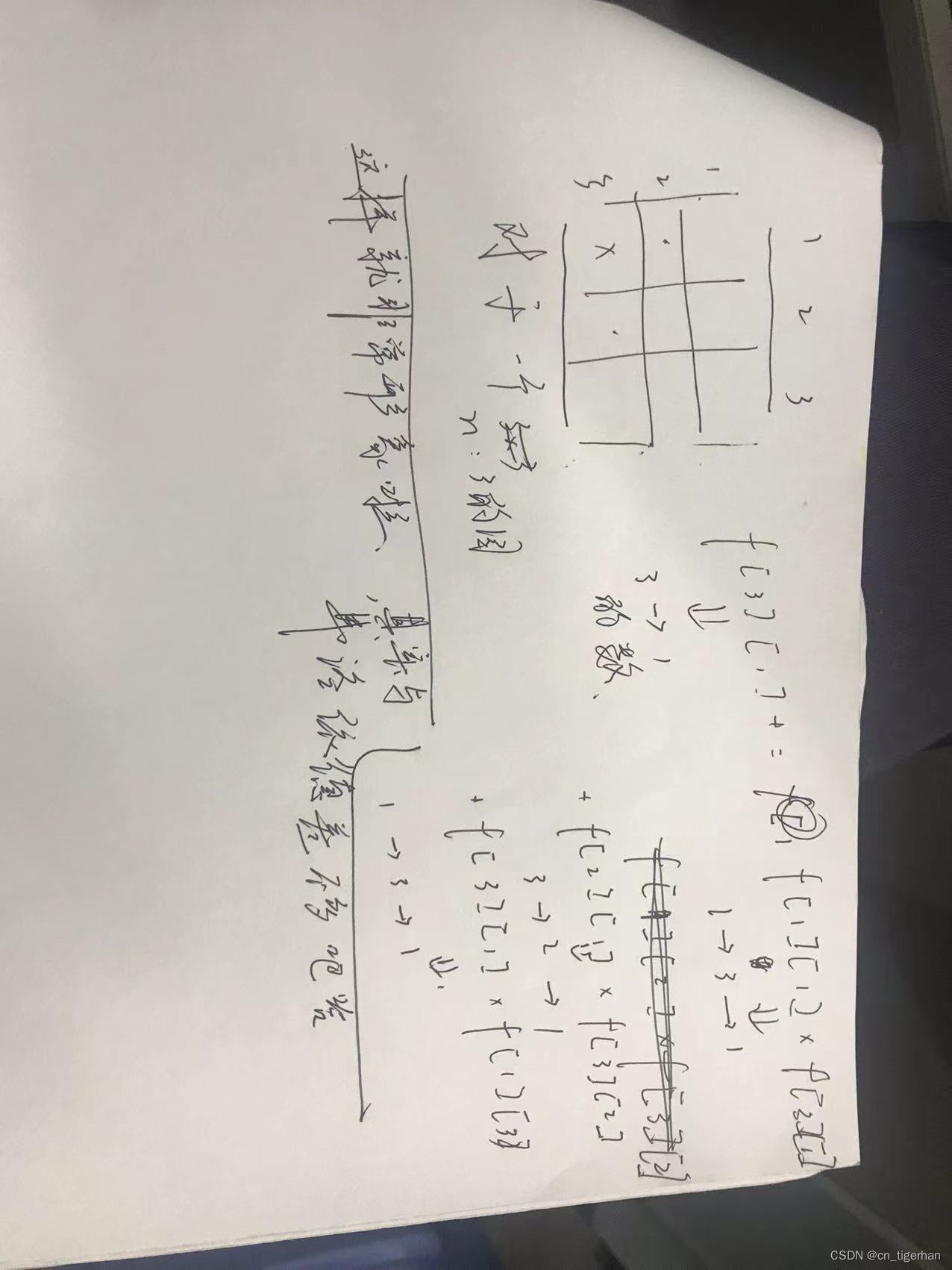
在这里插入图片描述
能看懂否？若不行还是算了吧qwq。理论上将其实就是枚举中转点（确实像佛洛依德），然后其他点到3的路径数是会算上的不然自己手推去，所以不用在意。
那么说回题目，我们不妨尝试理解题面：其实就是让你求有多少条长度为t的路径，但是有一个特殊条件：不能走过一条边以后又立刻反着走一次（如果两次经过同意条边中间隔了别的边是可以的），所以也许大概我们可以先用dp处理出来，然后再用矩阵加速。那么小细节dp的时候注意我们要用边，所以我们构建矩阵的时候也是用边。

#include<bits/stdc++.h>
using namespace std;
int n,m,k,len=1,last[100001],mod=45989;
struct pp
{
	int x,y,next;
};pp p[100001];
struct node
{
	int n,m,w[250][250];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{
				for(int k=1;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+x.w[i][k]*y.w[k][j]%mod)%mod;//printf("%d\n",rt.w[i][j]);
			}
		}
		return rt;
	};
};node ans,base,A,B;
void init(node &now,int x)
{
	now.n=now.m=x;memset(now.w,0,sizeof(now.w)); 
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
void ins(int x,int y)
{
	int now=++len;
	p[now]={x,y,last[x]};last[x]=now; 
	return ;	
}
node power(node x,int k)
{
	node rt;init(rt,len);
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1; 
	}
	return rt;
}
int main()
{
	memset(last,-1,sizeof(last));//printf("*");
	int ST,ED;scanf("%d%d%d%d%d",&n,&m,&k,&ST,&ED);ST++,ED++;
	for(int i=1;i<=m;i++)
	{
		int x,y;scanf("%d%d",&x,&y);x++,y++;
		ins(x,y);ins(y,x); 
	}B.n=1;B.m=A.n=A.m=len;
	for(int i=1;i<=len;i++)
	{
		int x=p[i].y;
		for(int j=last[x];j!=-1;j=p[j].next)	
		{//printf("%d %d ",i,j);
			if((i^1)==j) continue ;
			A.w[i][j]++;
		}
	}
	for(int i=last[ST];i!=-1;i=p[i].next) B.w[1][i]+=1;
	ans=B*power(A,k-1);int sum=0;
	for(int i=last[ED];i!=-1;i=p[i].next) (sum+=ans.w[1][i^1])%=mod;
	printf("%d",sum%mod);
	return 0;
}

P3758 [TJOI2017]可乐

#include<bits/stdc++.h>
using namespace std;
int n,m,k,mod=2017;
struct pp
{
	int x,y,next;
};pp p[100001];
struct node
{
	int n,m,w[250][250];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=0;i<=rt.n;i++)
		{
			for(int j=0;j<=rt.m;j++)
			{
				for(int k=0;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+x.w[i][k]*y.w[k][j]%mod)%mod;//printf("%d\n",rt.w[i][j]);
			}
		}
		return rt;
	};
};node ans,A,B;
void init(node &now,int x)
{
	now.n=now.m=x;memset(now.w,0,sizeof(now.w)); 
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
node power(node x,int k)
{
	node rt;init(rt,m);
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1;
	}
	return rt;
}
int main()
{ 	
	scanf("%d%d",&n,&m);A.n=A.m=ans.n=ans.m=n;
	for(int i=1;i<=m;i++) 
	{
		int x,y;scanf("%d%d",&x,&y);
		A.w[x][y]=A.w[y][x]=1;
	}
	for(int i=0;i<=n;i++) A.w[i][i]=1;
	for(int i=1;i<=n;i++) A.w[i][0]=1;
	scanf("%d",&k);ans=power(A,k);int sum=0;
	for(int i=0;i<=n;i++) (sum+=ans.w[1][i])%=mod;
	printf("%d",sum);
	return 0;  
}

P2886 [USACO07NOV]Cow Relays G矩阵优化弗洛伊德这这这，很高级的样子

#include<bits/stdc++.h>
using namespace std;
int n,m,id[2000001],tot=0;
struct pp
{
	int x,y,next;
};pp p[2000001];
struct node
{
	int n,m,w[200][200];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,63,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{
				for(int k=1;k<=x.m;k++) rt.w[i][j]=min(rt.w[i][j],x.w[i][k]+y.w[k][j]);//printf("%d\n",rt.w[i][j]);
			}
		}
		return rt;
	};
};node ans,A,B;
node power(node x,int k)
{
	node rt=x;k--;
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1;
	}
	return rt;
}
int main()
{
	memset(A.w,63,sizeof(A.w));memset(id,0,sizeof(id));
	int k,ST,ED;scanf("%d%d%d%d",&k,&m,&ST,&ED);
	for(int i=1;i<=m;i++)
	{
		int x,y,c;scanf("%d%d%d",&c,&x,&y);
		if(!id[x]) id[x]=++tot;
		if(!id[y]) id[y]=++tot;
		A.w[id[x]][id[y]]=A.w[id[y]][id[x]]=min(A.w[id[x]][id[y]],c);
	}
	A.n=A.m=tot+1;ans=power(A,k);
	printf("%d",ans.w[id[ST]][id[ED]]); 
	return 0;
}

介绍一个矩阵+拆点的：P4159 [SCOI2009] 迷路

#include<bits/stdc++.h>
using namespace std;
int n,m,k,mod=2009;
struct node
{
	int n,m,w[101][101];
	friend node operator *(const node &x,const node &y)
	{
		node rt;rt.n=x.n,rt.m=y.m;memset(rt.w,0,sizeof(rt.w));
		for(int i=1;i<=rt.n;i++)
		{
			for(int j=1;j<=rt.m;j++)
			{
				for(int k=1;k<=x.m;k++) rt.w[i][j]=(rt.w[i][j]+x.w[i][k]*y.w[k][j])%mod;//printf("%d",rt.w[i][j]);
			}
		}
		return rt;
	};
};node ans,A;
void init(node &now,int x)
{
	now.n=now.m=x;memset(now.w,0,sizeof(now.w));
	for(int i=1;i<=x;i++) now.w[i][i]=1;
	return ;
}
node power(node x,int k)
{
	node rt;init(rt,m); 
	while(k)
	{
		if(k&1) rt=rt*x;
		x=x*x;k>>=1;
	}
	return rt;
}
inline int getpos(const int &u, const int &i)
{
	return u + i * n; 
}
int main()
{
	scanf("%d%d",&n,&k);m=n*9;A.n=A.m=m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=8;j++) A.w[getpos(i,j)][getpos(i,j-1)]=1;
		for(int j=1;j<=n;j++)
		{
			int x;scanf("%1d",&x); 
			if(x) A.w[i][getpos(j,x-1)]=1;
		}
	} 
	ans=power(A,k);printf("%d",ans.w[1][n]);
	return 0;
 }

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/20916.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

kubernetes介绍与资源管理

kubernetes介绍与资源管理

#kubernetes介绍与资源管理 1应用部署方式演变 在部署应用程序的方式上&#xff0c;主要经历了三个时代&#xff1a; 传统部署&#xff1a;互联网早期&#xff0c;会直接将应用程序部署在物理机上 优点&#xff1a;简单&#xff0c;不需要其它技术的参与 缺点&#xff1a;…
阅读更多...
CMSC5713-IT项目管理之人力资源管理Human Resources Management

CMSC5713-IT项目管理之人力资源管理Human Resources Management

文章目录9.1. Introduction9.1.1. Motivation Theories9.1.2. Influence and Power9.1.3. Motivating Team9.2. Project Human Resource Management9.3. Human Resource Planning9.3.1. Project Organization Charts9.3.2. Responsibility Assignment Matrices9.3.2.1. RACI Ch…
阅读更多...
锐捷BFD基础实验配置

锐捷BFD基础实验配置

目录 BFD与静态路由联动 BFD与静态路由联动&#xff08;单跳&#xff09; BFD与静态路由联动&#xff08;多跳&#xff09; BFD与动态路由联动 配置BFD与OSPF联动 配置BFD与BGP联动 BFD与静态路由联动 BFD联动静态路由注意事项 1、配置需要联动的静态路由时&#xff0c…
阅读更多...
Java线程池

Java线程池

自定义线程池 1. 简介 1.1 引入原因 1. 一个任务过来&#xff0c;一个线程去做。如果每次过来都创建新线程&#xff0c;性能低且比较耗费内存 2. 线程数多于cpu核心&#xff0c;线程切换&#xff0c;要保存原来线程的状态&#xff0c;运行现在的线程&#xff0c;势必会更加耗…
阅读更多...
idea创建spring boot工程及配置

idea创建spring boot工程及配置

目录 一、dea 创建spring boot工程 二、打包 三、启动配置文件 一、dea 创建spring boot工程 new project 选择Spring Initializr ,Type&#xff1a;选择Maven&#xff0c;Java 8, Packagin 选择Jar。然后点击next 添加依赖&#xff1a; 选择Sprint Boot版本&#xff0c;选…
阅读更多...
差分约束算法

差分约束算法

差分约束是为了解决这样一组不等式问题&#xff1a; 这个咋解决》我们来看 对于某个下标k而言&#xff0c;提取出关于其的所有不等式&#xff0c;&#xff08;其中xk在第一个),也就是 xk-x1<m1 xk-x2<m2 xk-x3<m3....对于这些不等式相当于是 xk取min(x1m1,x2m2,x3m3…
阅读更多...
面试常问：HTTPS的加密过程 ----- 光明和黑暗的恩怨情仇

面试常问：HTTPS的加密过程 ----- 光明和黑暗的恩怨情仇

目录 关于运营商劫持 &#xff1a; 什么是运营商劫持?? 什么是运营商? 为什么要劫持? 如何劫持? 劫持的危害 互联网公司怎么办? HTTPS 什么是HTTPS 一些概念&#xff1a; HTTPS加密 1. 对称加密&#xff1a; 2. 非对称加密 3. 非对称加密对称加密 4. 加密…
阅读更多...
基于java+ssm购物商城网站系统-计算机毕业设计

基于java+ssm购物商城网站系统-计算机毕业设计

项目介绍 乐优购物商城是商业贸易中的一条非常重要的道路&#xff0c;可以把其从传统的实体模式中解放中来&#xff0c;网上购物可以为消费者提供巨大的便利。通过乐优购物商城这个平台&#xff0c;可以使用户足不出户就可以了解现今的流行趋势和丰富的商品信息&#xff0c;为…
阅读更多...
请求跨域问题

请求跨域问题

在前端请求接口时&#xff0c;出现跨域是很常见的问题&#xff0c;跨域的解决方法也很多&#xff0c;但是目前通用的是以下两种方式&#xff1a; 开发环境生产环境在服务端配置 CORS在服务端配置 CORS配置开发服务器代理&#xff0c;比如 vite-server.proxy配置生产服务器代理…
阅读更多...
Debezium的增量快照

Debezium的增量快照

GreatSQL社区原创内容未经授权不得随意使用&#xff0c;转载请联系小编并注明来源。GreatSQL是MySQL的国产分支版本&#xff0c;使用上与MySQL一致。作者&#xff1a; 如常 Debezium Incremental snapshotting Introduction CDC&#xff08;Change-Data-Capture&#xff09;正…
阅读更多...
Java之反射相关知识补充

Java之反射相关知识补充

Java之反射一、概述1、静态语言和动态语言1.1 静态语言1.2 动态语言2、Reflection(反射)2.1 介绍2.2 流程2.3 Java反射机制提供的功能2.4 优缺点&#xff08;1&#xff09;优点&#xff08;2&#xff09;缺点2.5 反射相关主要API2.6 示例二、反射相关操作1、获取Class类的实例1…
阅读更多...
第十二节：String类【java】

第十二节：String类【java】

目录 &#x1f4d8;1.1 字符串构造方法 &#x1f4d2;1.2 String对象怎样比较 &#x1f4dc;1.2.1 引用类型 比较的是引用中的地址。 &#x1f4c4;1.2.2 boolean equals(Object anObject) 方法&#xff1a;比较怕两个引用所指的对象当中的内容是否一致 &#x1f4d1;1.2…
阅读更多...
企业级nginx使用

企业级nginx使用

企业级nginx使用 nginx实现平滑升级 [rootlnmp nginx-1.16.0]# cd /usr/local/nginx/sbin/ [rootlnmp sbin]# ls nginx nginx.old [rootlnmp sbin]# ./nginx -v nginx version: nginx/1.16.0 [rootlnmp sbin]# ./nginx.old -v nginx version: nginx/1.14.2 [rootlnmp sbin]#操…
阅读更多...
物联网开发笔记（49）- 使用Micropython开发ESP32开发板之控制RGB全彩LED模块

物联网开发笔记（49）- 使用Micropython开发ESP32开发板之控制RGB全彩LED模块

一、目的 这一节我们学习如何使用我们的ESP32开发板来控制RGB全彩LED模块。 二、环境 ESP32 RGB全彩LED模块 Thonny IDE 几根杜邦线 1&#xff0c;共阴极接线方法 2&#xff0c;共阳极接线方法 三、代码 1&#xff0c;亮指定的颜色&#xff0c;比如百度蓝。 我们使用取色…
阅读更多...
万字长文，精美插图，带你玩转redis

万字长文，精美插图，带你玩转redis

资料下载&#xff1a; 链接: https://pan.baidu.com/s/1ue4Bnv4b4ifp0S0I_yOJ_w?pwdd9x9 提取码: d9x9 Redis学习笔记 1. 认识Redis 1.1 什么是NoSQL&#xff1f; SQL是关系型数据库&#xff0c;NoSQL是非关系型数据库 下面是几种非关系型数据库及其优缺点和应用场景。 分类…
阅读更多...
[附源码]java毕业设计网上书店系统

[附源码]java毕业设计网上书店系统

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
【分隔结构】动宾分离

【分隔结构】动宾分离

动宾分离 动词 宾语 状语&#xff1a;如果宾语较长&#xff0c;状语较短&#xff0c;会转化为 动词 状语 宾语 While I disapprove of what you say, I would defend to the death your right to say it. 名词 引导词 主语 及物动词 You are the man that I will marry…
阅读更多...
【K8S】学习笔记（一）

【K8S】学习笔记（一）

K8S学习笔记一、Kubernetes1.1、K8S功能1.2、K8S架构组件1.2.1、架构细节1.3、K8S核心概念1.3.1、Pod1.3.2、Volume1.3.3、Controller1.3.4、Deployment1.3.5、Service1.3.6、Label1.3.7、Namespace1.3.8、API二、搭建K8S2.1、K8S搭建规划2.1.1、单master集群2.1.2、多master集…
阅读更多...
Html5的新增特性

Html5的新增特性

Html5的新增特性主要是针对以前的不足&#xff0c;增加了一些新的标签&#xff0c;新的表单和新的表单属性等。 这些新特性都有兼容性问题&#xff0c;基本是IE9以上版本的浏览器才支持&#xff0c;如果不考虑兼容性问题&#xff0c;可以大量使用这些新特性。 声明&#xff1…
阅读更多...
m基于迫零ZF准则的通信均衡器的matlab仿真

m基于迫零ZF准则的通信均衡器的matlab仿真

目录 1.算法概述 2.仿真效果预览 3.MATLAB部分代码预览 4.完整MATLAB程序 1.算法概述 在数字通信系统中&#xff0c;码间串扰和加性噪声是造成信号传输失真的主要因素&#xff0c;为克服码间串扰&#xff0c;在接收滤波器和抽样判决器之间附加一个可调滤波器&#xff0c;用…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023