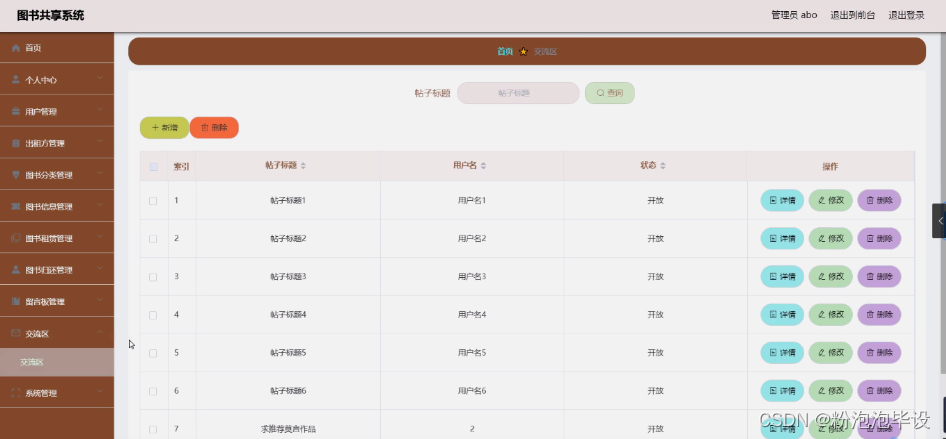
目录
1.算法概述
2.仿真效果预览
3.MATLAB部分代码预览
4.完整MATLAB程序
1.算法概述
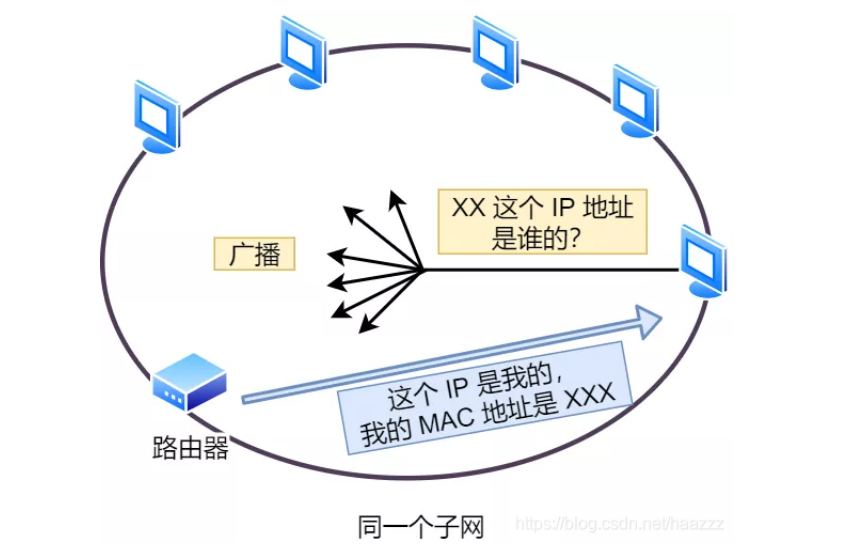
在数字通信系统中,码间串扰和加性噪声是造成信号传输失真的主要因素,为克服码间串扰,在接收滤波器和抽样判决器之间附加一个可调滤波器,用以校正(或补偿)这些失真。对系统中线性失真进行校正的过程称为均衡,实现均衡的滤波器称为均衡滤波器。
ZF均衡算法是一种根据峰值失真准则推导而来的线性均衡算法。将OFDM系统接收端的频域输出方程组用矩阵表示为
Y=HX+W
其中W为加性高斯白噪声。为了得到发送端的发送信号X,最简单的实现方法是将Y乘以矩阵的 逆,即:
![]()
所以迫零均衡器为:
![]()
但当传输信道具有较深的频谱凹陷点时,H(-1)一般不存在,此时一般由其伪逆H+来代替,即
ZF算法有个很大的缺点,没有对噪声进行消除,反而会放大噪声,当信噪比比较低时,性能会非常不好。![]()
由于实际的限带信道的传递函数往往是非理想的,且经常是事变的、未知的,因而系统特性不符合奈窐斯特准则,导致在接受端抽样时刻存在码间干扰,使得系统误码性能下降。为此,要考虑在信道传递函数是非理想情况,且信号在信道传输中受到加性白高斯噪声干扰条件下的接收机的设计问题。本文提出了基于迫零算法的信道均衡器,对迫零线性均衡器进行了理论分析,并在Matlab中进行仿真得到了良好的仿真结果。
迫零算法是由Lucky于1965年提出的,他在分析中略去了信道的加性噪声,所以在实际存在噪声的情况下由该算法得到的解不一定是最佳的,但它易于实现。
所以在信道的频率响应特性比较平坦,所引起的码间干扰不太严重的情况下,由该算法可达到信道均衡的效果。在横向滤波器的延迟单元N为无穷多个的理想线性均衡条件下:

在k为其它值时,hk可能是非零值,构成均衡器输出端的残留码间干扰。在本文的下一章,我们将重点介绍基于迫零的均衡系统的设计与实现。
2.仿真效果预览
matlab2022a仿真
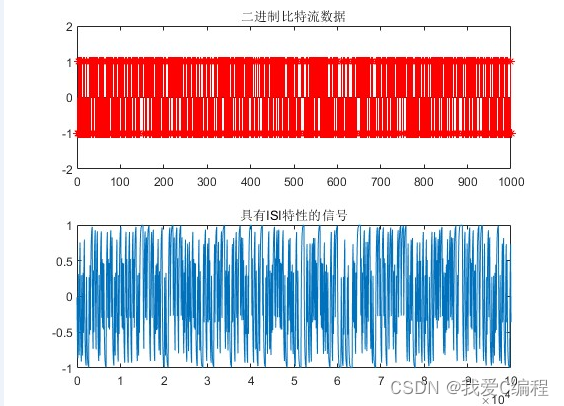
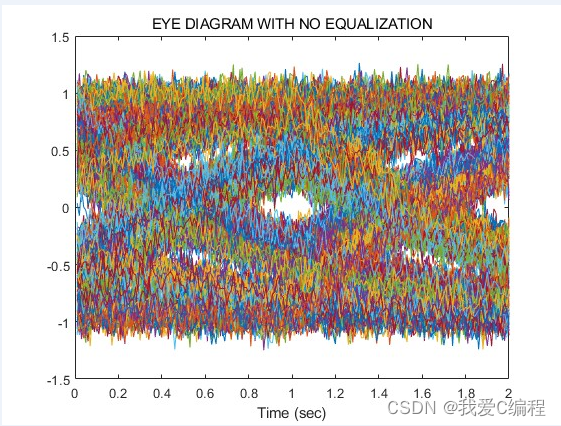
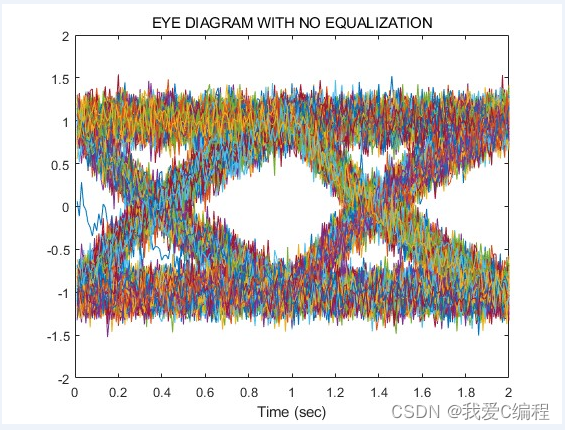
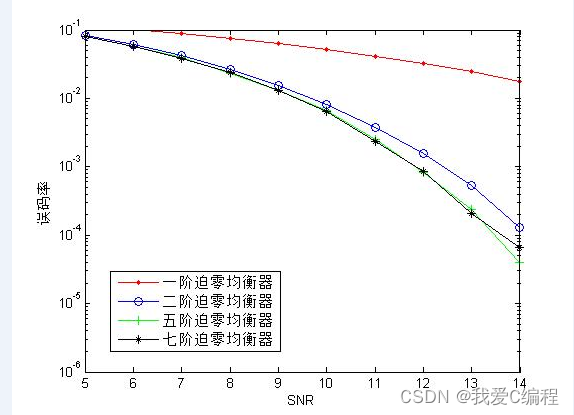
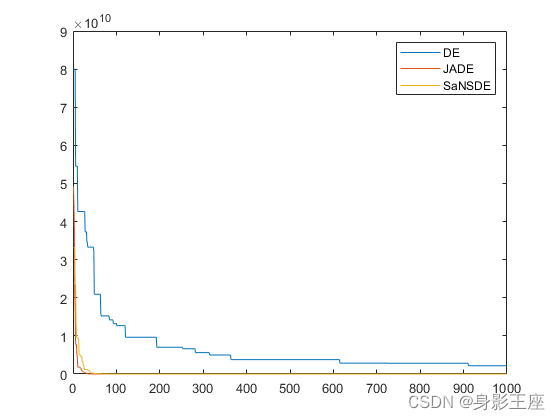
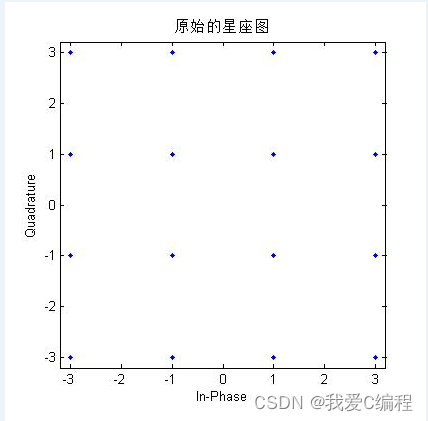
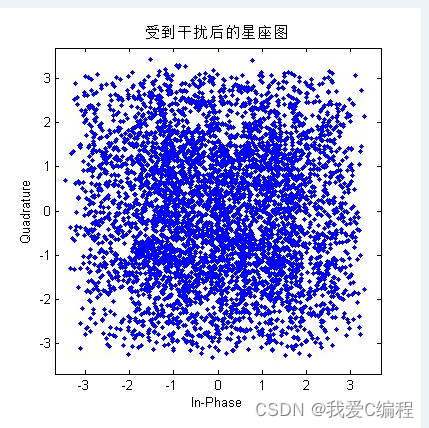
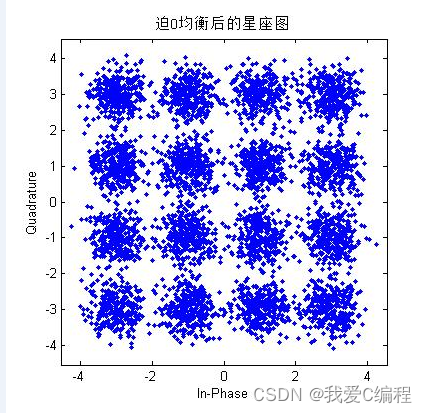
同上面星座图和误码率曲线的分析,我们基本可以知道,系统在1阶迫零的情况下,性能较差,无法正常的工作,此时其误码率也非常的高,当阶数增加到2阶的时候,系统的性能得到了明显的 改善,当系统阶数更高的时候,系统效果良好,误码率很低,基本达到应用级别。
3.MATLAB部分代码预览
function ZF_filter = filters_ZF();
%加载一些有用的参数;
load r0;
load filter_pluse;
load nT;
load nx;
load nc;
load y;
load signal_with_ISI;
load signal_with_ISI_noise;
load cT;
load Ne;
load filter_pluse_sample;
load ZF_out;
%ZF调整
nw = length(ZF_out);
Z = [1; zeros(nT-1,1)];
hzf= 0;
LS = 0;
y = 0;
%均衡滤波器的系数的调整
hzf = kron(ZF_out, Z);
save hzf;
LS = conv(signal_with_ISI_noise, hzf);
save LS;
ZF_filter = LS((Ne*nT+1):(length(LS)-(Ne+1)*nT)+1);
save ZF_filter;
figure
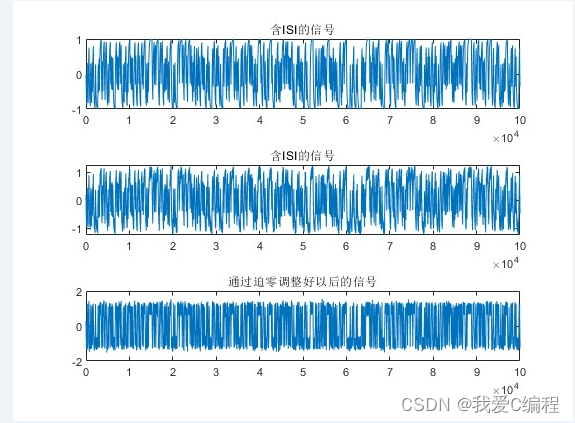
subplot(311);plot(signal_with_ISI) ;title('含ISI的信号');
subplot(312);plot(signal_with_ISI_noise);title('含ISI的信号');
subplot(313);plot(ZF_filter) ;title('通过迫零调整好以后的信号');
eyes(ZF_filter);
01_027_m4.完整MATLAB程序
matlab源码说明_我爱C编程的博客-CSDN博客
V