星型智能反射面辅助NOMA系统的遍历率分析 原文链接

1 STAR-RIS

全称(Simultaneously transmitting and reflecting reconfigurable intelligent surface)，星型智能反射面。
特点：覆盖范围可达到360°；可以同时反射（reflection mode）和折射（refraction mode）
STAR-RIS具体可参考这篇文章

2 摘要

本文分析了一个同时发射和反射的可重构智能表面（STAR-智能反射面）辅助非正交多址(NOMA)系统的遍历速率。
在该系统中，由于障碍物，从基站到小区边缘用户的直接链路是非视距链路，而STAR-智能反射面用于向这些小区边缘用户提供视距链路。 通过将复合信道功率增益的分布拟合为Gamma分布，导出了小区边缘用户的遍历率和高信噪比斜率的闭式表达式。
数值结果表明：

• （1）各态历经率随星智能反射面元素数目的增加而增加，高信噪比斜率固定为常数；
• （2）STAR-智能反射面辅助NOMA系统比传统的智能反射面辅助NOMA系统具有更高的遍历率。

3 系统模型

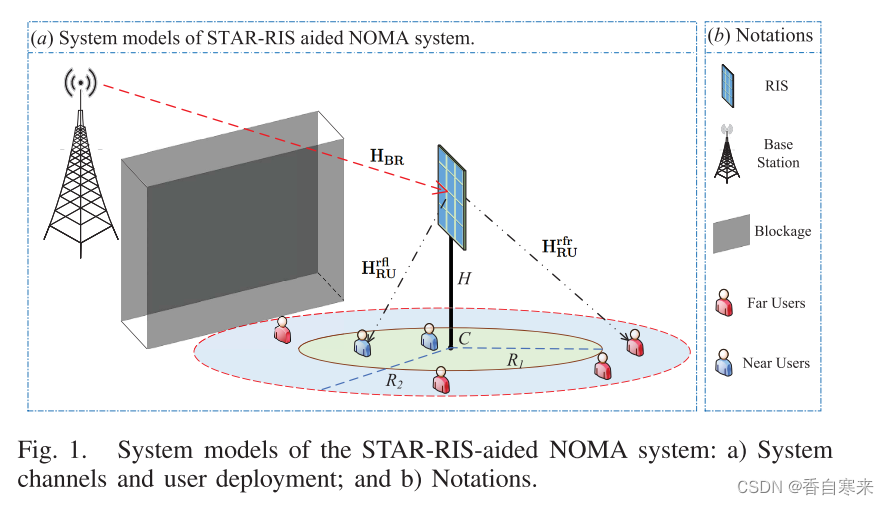
3.1 信道

为了刻画实际快速衰落信道的统计特性，考虑了一种更实际的信道，如Nakagami-M衰落。 该系统的信道模型用Gamma分布模拟，便于多小区性能分析。

3.2 用户位置

我们利用齐次泊松点过程来建模用户的位置。
近场用户与远场用户的** 概率密度函数 (PDF：probability density function)**分别为
$$f_{d_{\text{near }}}(x)=\frac{\partial }{\partial x}\frac{\pi x^2}{\pi R_1^2}=\frac{2x}{R_1^2}$$
$$f_{d_{far}}(x)=\frac{\partial }{\partial x}\frac{\pi \left(x^2-R_1^2\right)}{\pi \left(R_2^2-R_1^2\right)}=\frac{2x}{R_2^2-R_1^2}$$

3.3 ES（Energy Splitting）能量分裂协议

具体看作者的另一篇文章，有具体描述和时间切换（TS：time switching）、**模式切换（MS：mode switching ）**对比。
在这里为了避免ES协议改变连续干扰消除(SIC)的排列顺序 ，反射系数和折射系数分别为${\beta }_n^{rfl}$和${\beta }_n^{rfr}$，且${\beta }_n^{rfl}+{\beta }_n^{rfl}=1$。

3.4 NOMA

为了最大化每个用户的增益并考虑单播传输，考虑采用NOMA用户对，近场用户采用SIC，远场用户直接解码信号。
在这里功率分配系数分别为${\alpha }_{near}$和${\alpha }_{far}$，且${\alpha }_{near}+{\alpha }_{far}=1$。

3.5 信道模型

基站BS通过STAR-RIS到用户UE的反射与折射信道为
$$\left|h_{rfl}\right|=\left|{\mathbf{H}}_{\mathbf{R}\mathbf{U}}^{\mathrm{r}\mathrm{f}\mathrm{l}}{}^T{\mathbf{\Theta }}_{\mathbf{r}\mathbf{f}\mathbf{l}}{\mathbf{H}}_{\mathrm{B}\mathrm{R}}\right|,\left|h_{rfr}\right|=\left|{\mathbf{H}}_{\mathbf{R}\mathbf{U}}^{\mathrm{r}\mathrm{f}\mathrm{r}}{}^T{\mathbf{\Theta }}_{\mathbf{r}\mathbf{f}\mathbf{r}}{\mathbf{H}}_{\mathbf{B}\mathbf{R}}\right|$$

${\Theta }_{\mathbf{r}\mathbf{f}\mathbf{l}}$和${\Theta }_{\mathbf{r}\mathbf{f}\mathbf{r}}$为对角相移矩阵；${\mathbf{H}}_{\mathbf{R}\mathbf{U}}^{\mathrm{r}\mathrm{f}\mathrm{l}}$等为反射用户与BS之间信道

3.6 信干噪比

对于近场用户，采用SIC；远场用户采取直连。
$$\begin{array}{rl}{\gamma }_{\text{near }}^{SIC}& =\frac{P_t{a}_{\text{far }}{\left(d_{\text{near }}^2+H^2\right)}^{-\frac{\alpha }{2}}{d}_{BR}^{-\alpha }{\left|h_k\right|}^2}{P_t{a}_{\text{near }}{\left(d_{\text{near }}^2+H^2\right)}^{-\frac{\alpha }{2}}{d}_{BR}^{-\alpha }{\left|h_k\right|}^2+{\sigma }^2},\\ {\gamma }_{\text{near }}& =\frac{P_t{a}_{\text{near }}{\left(d_{\text{near }}^2+H^2\right)}^{-\frac{\alpha }{2}}{d}_{BR}^{-\alpha }{\left|h_k\right|}^2}{{\sigma }^2},\\ {\gamma }_{\text{far }}& =\frac{P_t{a}_{\text{far }}{\left(d_{\text{far }}^2+H^2\right)}^{-\frac{\alpha }{2}}{d}_{BR}^{-\alpha }{\left|h_j\right|}^2}{P_t{a}_{\text{near }}{\left(d_{\text{far }}^2+H^2\right)}^{-\frac{\alpha }{2}}{d}_{BR}^{-\alpha }{\left|h_j\right|}^2+{\sigma }^2},\end{array}$$
$P_t$为用户的传输功率；${\sigma }^2$为AWGN信道噪声的方差；$\alpha$为路径损耗指数。当近场用户为反射用户时，k=rfl and j=rfr；当近场用户为折射用户时，k=rfr and j=rfl。

4 仿真

4.1 遍历率分析

遍历率表示平均可达速率。$$\begin{array}{rl}{R}_{\text{near }}& =\mathbb{E}\left[\log \left(1+{\gamma }_{\text{near }}\right)\right]u\left({\gamma }_{\text{near }}^{SIC}-{\gamma }_{\text{th }}^{SIC}\right),\\ R_{\text{far }}& =\mathbb{E}\left[\log \left(1+{\gamma }_{\text{far }}\right)\right],\end{array}$$
$\mathbb{E}$为期望函数；$u(t)$为阶跃函数；${\gamma }_{\text{th }}^{SIC}$为SIC阈值。