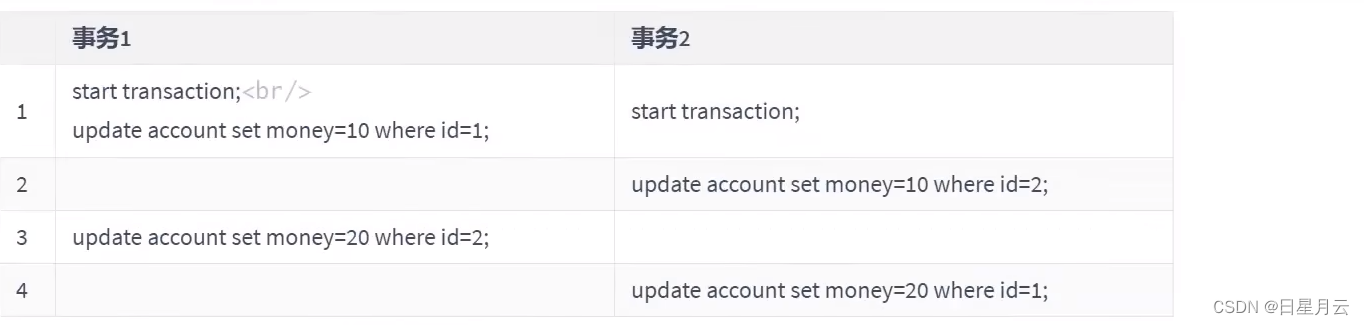
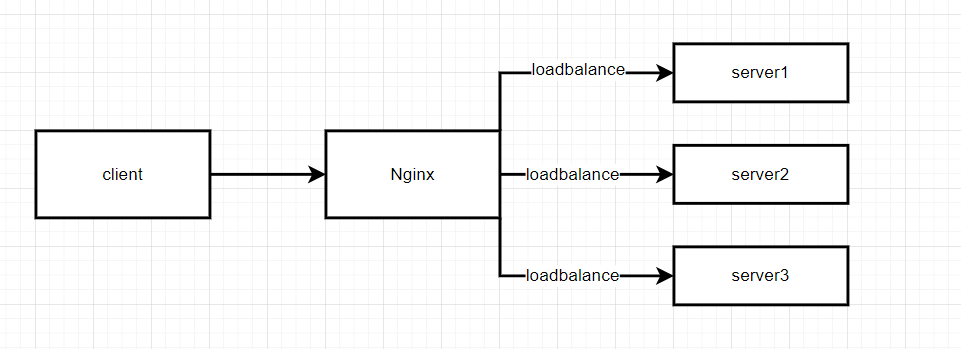
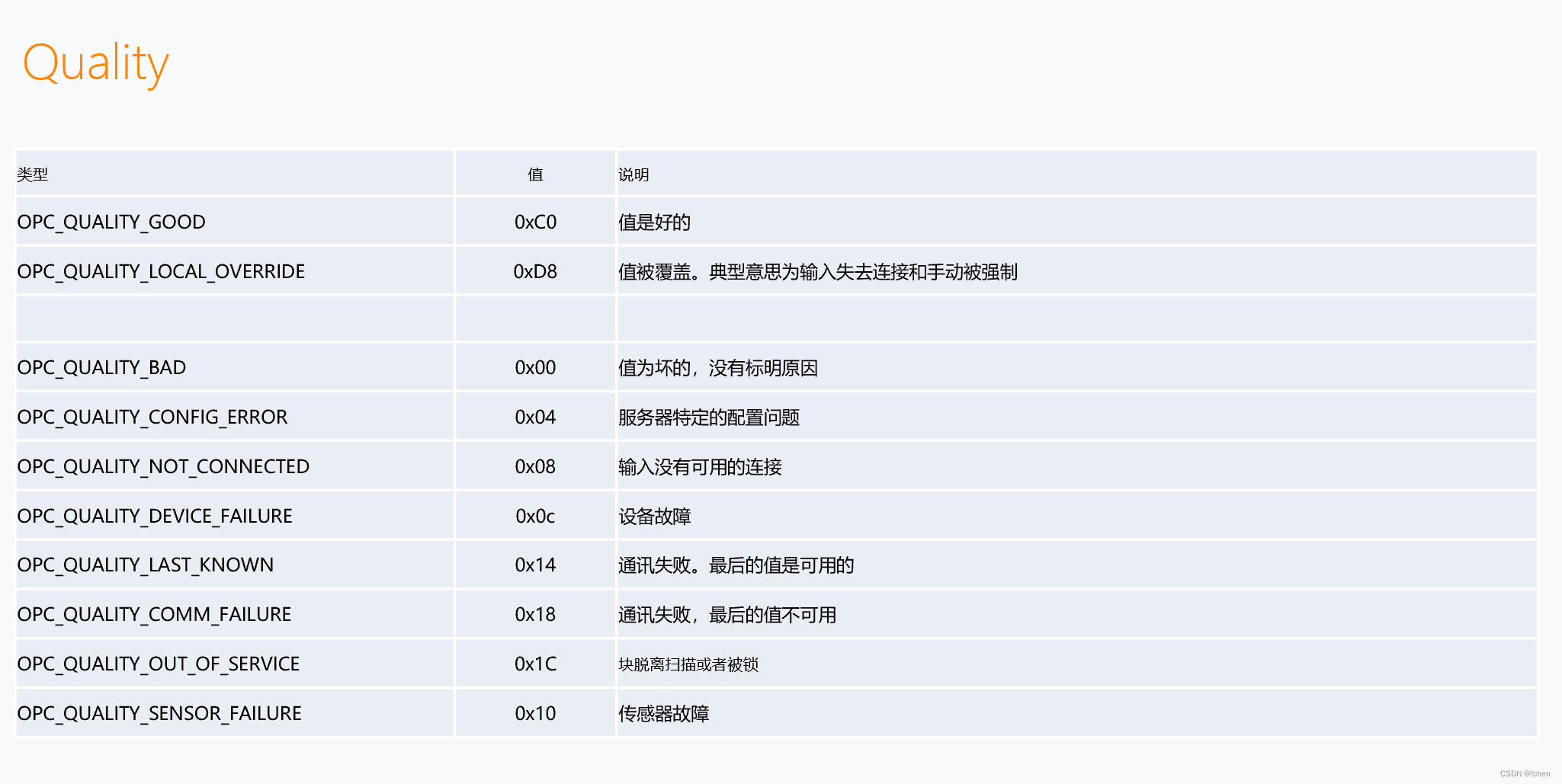
题目如下：

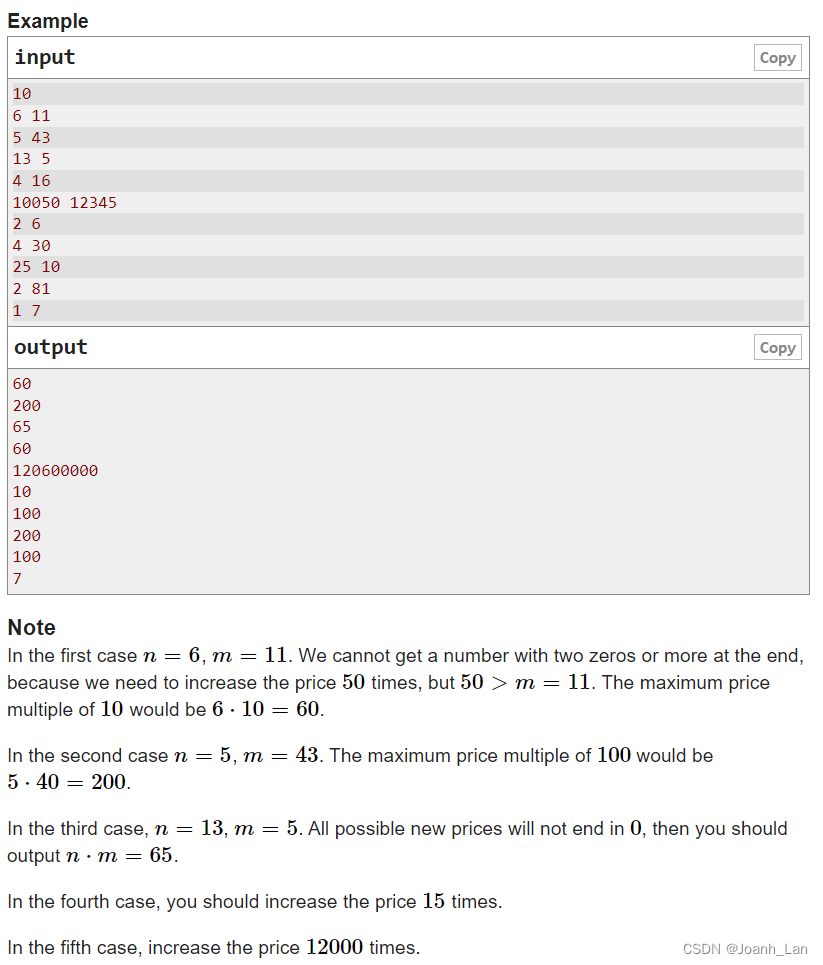
思路 or 题解：

我们先考虑如何操作使结尾有最多的 0
我们不难发现：

2 * 5 = 10
10 = 10

我们是否只需要考虑 2 与 5 的贡献就行了
答案是肯定的！！！

约定：
$cn{t}_5因数5的个数$
$cn{t}_2因数2的个数$

如果 $cn{t}_5>cn{t}_2$ 我们通过 2 去凑更多的 0，也就是 $\times 2$
如果 $cn{t}_2>cn{t}_5$ 我们通过 5 去凑更多的 0，也就是 $\times 5$

最后 通过 10 去凑更多的 0，也就是 $\times 10$

我们再考虑如何 构造最大的数并且 后缀 0 的个数最多
我们通过上面操作 可以使 $n\times x$ 成为后缀 0 个数最多 的一个合法数
如何才可以取最大呢？
$k\times x\times n(k\ge 1)$ 不会改变 后缀 0 个数
就是 将 $x$ 变大就行， 让 $x$ 取得最大值
$x_{max}=m/x\times x$

所以答案就是：
$n\ast m/x\times x$

AC代码：

#define int long long
//#define ll long long
#define PII pair<int, int>
#define px first
#define py second
typedef std::mt19937  Random_mt19937;
Random_mt19937  rnd(time(0));
using namespace std;
const int mod = 1e9 + 7;
const int N = 100009;
int n, m;
void solve()
{
    cin >> n >> m;
    int cnt2 = 0, cnt5 = 0;
    int tt = n;
    while (tt % 2 == 0)
        cnt2++, tt /= 2;
    tt = n;
    while (tt % 5 == 0)
        cnt5++, tt /= 5;
    int x = 1;
    while (cnt5 > cnt2 && x * 2 <= m)
        cnt5--, x *= 2;
    while (cnt5 < cnt2 && x * 5 <= m)
        cnt2--, x *= 5;

    while (x * 10 <= m)
        x *= 10;
    cout << m / x * x * n << '\n';
}
signed main()
{
    buff;
    int _;
    cin >> _;
    while (_--)
        solve();
}