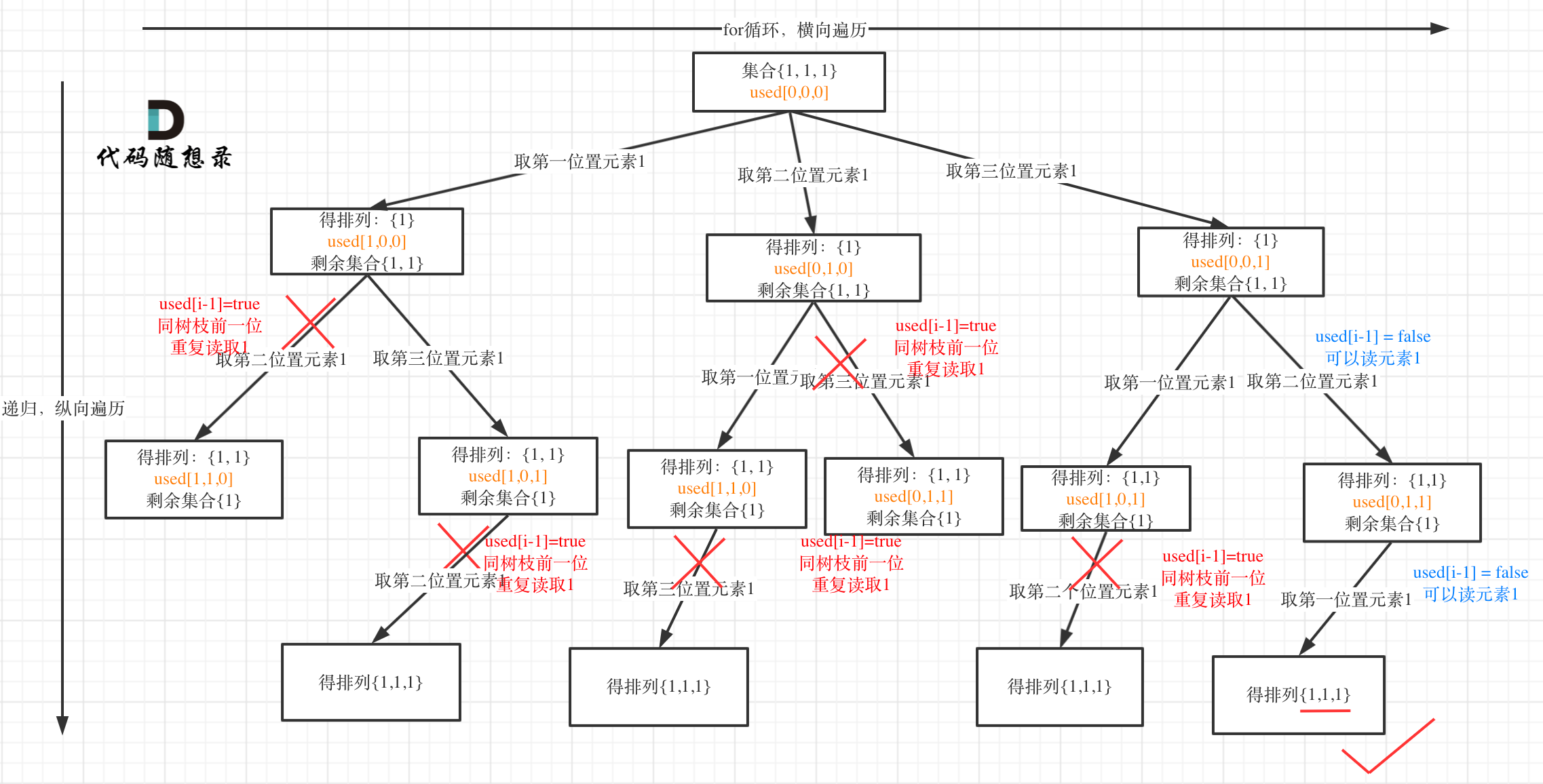
代码 

#include <algorithm>
#include <cassert>
#include <functional>
#include <map>
#include <memory>
#include <queue>
#include <set>
#include <unordered_set>
#include <vector>

namespace jc {

    template <typename K, typename V>
    struct DAGNode {
        K k;
        V v;
        std::set<DAGNode<K, V>*> in;
        std::set<DAGNode<K, V>*> out;
    };

    template <typename K, typename V>
    class DAGGraph {
    public:
        bool AddEdge(const K& from, const K& to);

        V& operator[](const K& key);

        bool Exist(const K& key) const;

        void Clear();

        std::size_t Size() const;

        void Walk(std::function<void(const K& k, const V& v)> f,
            bool start_from_head = true);

        void WalkHeads(std::function<void(const K& k, const V& v)> f);

        void WalkTails(std::function<void(const K& k, const V& v)> f);

        std::unordered_set<K> NextKeys();

        std::unordered_set<K> NextKeys(const K& key);

    private:
        bool IsCyclic(const DAGNode<K, V>& from, const DAGNode<K, V>& to) const;

        void RefreshWalkSequences();

        std::vector<std::set<K>> ConnectedComponents() const;

        void DFS(const K& k, std::unordered_set<K>* visited,
            std::set<K>* connected_components) const;

        std::vector<K> TopologicalSequence(const std::set<K>& connected_components,
            bool start_from_head) const;

    private:
        std::map<K, DAGNode<K, V>> bucket_;
        std::unordered_set<K> heads_;
        std::unordered_set<K> tails_;
        std::vector<std::vector<K>> sequences_start_from_head_;
        std::vector<std::vector<K>> sequences_start_from_tail_;

    private:
        bool allow_modify_ = true;
        std::vector<std::vector<K>> sequences_start_from_head_for_next_;
        std::unordered_set<K> current_heads_for_next_;
    };

    template <typename K, typename V>
    inline bool DAGGraph<K, V>::AddEdge(const K& from, const K& to) {
        assert(allow_modify_);
        if (from == to || !bucket_.count(from) || !bucket_.count(to) ||
            IsCyclic(bucket_.at(from), bucket_.at(to))) {
            return false;
        }
        bucket_.at(from).out.emplace(&bucket_.at(to));
        bucket_.at(to).in.emplace(&bucket_.at(from));
        heads_.erase(to);
        tails_.erase(from);
        sequences_start_from_head_.clear();
        sequences_start_from_tail_.clear();
        return true;
    }

    template <typename K, typename V>
    inline V& DAGGraph<K, V>::operator[](const K& key) {
        if (!bucket_.count(key)) {
            assert(allow_modify_);
            bucket_[key].k = key;
            heads_.emplace(key);
            tails_.emplace(key);
            sequences_start_from_head_.clear();
            sequences_start_from_tail_.clear();
        }
        return bucket_.at(key).v;
    }

    template <typename K, typename V>
    inline bool DAGGraph<K, V>::Exist(const K& key) const {
        return bucket_.count(key);
    }

    template <typename K, typename V>
    inline void DAGGraph<K, V>::Clear() {
        allow_modify_ = true;
        bucket_.clear();
        heads_.clear();
        tails_.clear();
        sequences_start_from_head_.clear();
        sequences_start_from_tail_.clear();
    }

    template <typename K, typename V>
    inline std::size_t DAGGraph<K, V>::Size() const {
        return bucket_.size();
    }

    template <typename K, typename V>
    inline void DAGGraph<K, V>::Walk(std::function<void(const K& k, const V& v)> f,
        bool start_from_head) {
        if (sequences_start_from_head_.empty()) {
            RefreshWalkSequences();
        }
        const std::vector<std::vector<K>>& seqs_to_walk =
            start_from_head ? sequences_start_from_head_ : sequences_start_from_tail_;
        for (const std::vector<K>& seq : seqs_to_walk) {
            std::for_each(std::begin(seq), std::end(seq), [&](const K& key) {
                const DAGNode<K, V>& node = bucket_.at(key);
                f(node.k, node.v);
                });
        }
    }

    template <typename K, typename V>
    inline void DAGGraph<K, V>::WalkHeads(
        std::function<void(const K& k, const V& v)> f) {
        if (sequences_start_from_head_.empty()) {
            RefreshWalkSequences();
        }
        for (const std::vector<K>& seq : sequences_start_from_head_) {
            std::for_each(std::begin(seq), std::end(seq), [&](const K& key) {
                if (heads_.count(key)) {
                    const DAGNode<K, V>& node = bucket_.at(key);
                    f(node.k, node.v);
                }
                });
        }
    }

    template <typename K, typename V>
    inline void DAGGraph<K, V>::WalkTails(
        std::function<void(const K& k, const V& v)> f) {
        if (sequences_start_from_head_.empty()) {
            RefreshWalkSequences();
        }
        for (const std::vector<K>& seq : sequences_start_from_tail_) {
            std::for_each(std::begin(seq), std::end(seq), [&](const K& key) {
                if (tails_.count(key)) {
                    const DAGNode<K, V>& node = bucket_.at(key);
                    f(node.k, node.v);
                }
                });
        }
    }

    template <typename K, typename V>
    inline std::unordered_set<K> DAGGraph<K, V>::NextKeys() {
        assert(allow_modify_);  // allowed call once unless Clear()
        allow_modify_ = false;
        current_heads_for_next_ = heads_;
        if (sequences_start_from_head_.empty()) {
            RefreshWalkSequences();
        }
        return heads_;
    }

    template <typename K, typename V>
    inline std::unordered_set<K> DAGGraph<K, V>::NextKeys(const K& key) {
        assert(!allow_modify_);  // must call NextKeys() before
        assert(current_heads_for_next_.count(key));
        current_heads_for_next_.erase(key);

        std::unordered_set<K> res;
        for (std::vector<K>& seq : sequences_start_from_head_for_next_) {
            auto it = std::find(begin(seq), std::end(seq), key);
            if (it == std::end(seq)) {
                continue;
            }
            seq.erase(it);
            const std::set<DAGNode<K, V>*>& nodes = bucket_.at(key).out;
            for (DAGNode<K, V>* v : nodes) {
                const std::set<DAGNode<K, V>*>& prev_nodes = v->in;
                bool no_prev_node_in_seq =
                    std::all_of(std::begin(prev_nodes), std::end(prev_nodes),
                        [&](DAGNode<K, V>* in_node) {
                            return std::find(std::begin(seq), std::end(seq),
                                in_node->k) == std::end(seq);
                        });
                if (no_prev_node_in_seq) {
                    current_heads_for_next_.emplace(v->k);
                    res.emplace(v->k);
                }
            }
            break;
        }
        return res;
    }

    template <typename K, typename V>
    inline bool DAGGraph<K, V>::IsCyclic(const DAGNode<K, V>& from,
        const DAGNode<K, V>& to) const {
        std::queue<DAGNode<K, V>*> q;
        for (DAGNode<K, V>* v : from.in) {
            q.emplace(v);
        }

        std::unordered_set<DAGNode<K, V>*> visited;
        while (!q.empty()) {
            DAGNode<K, V>* node = q.front();
            q.pop();
            if (visited.count(node)) {
                continue;
            }
            if (node == &to) {
                return true;
            }
            visited.emplace(node);
            for (DAGNode<K, V>* v : node->in) {
                q.emplace(v);
            }
        }

        return false;
    }

    template <typename K, typename V>
    inline void DAGGraph<K, V>::RefreshWalkSequences() {
        sequences_start_from_head_.clear();
        sequences_start_from_tail_.clear();

        const std::vector<std::set<K>> connected_components = ConnectedComponents();
        for (const std::set<K>& x : connected_components) {
            const std::vector<K> seq_from_head = TopologicalSequence(x, true);
            const std::vector<K> seq_from_tail = TopologicalSequence(x, false);
            assert(!seq_from_head.empty());
            assert(!seq_from_tail.empty());
            sequences_start_from_head_.emplace_back(seq_from_head);
            sequences_start_from_tail_.emplace_back(seq_from_tail);
        }

        sequences_start_from_head_for_next_ = sequences_start_from_head_;
    }

    template <typename K, typename V>
    inline std::vector<std::set<K>> DAGGraph<K, V>::ConnectedComponents() const {
        std::vector<std::set<K>> res;
        std::unordered_set<K> visited;
        for (auto& x : bucket_) {
            std::set<K> tmp;
            DFS(x.second.k, &visited, &tmp);
            if (!tmp.empty()) {
                res.emplace_back(tmp);
            }
        }
        std::sort(std::begin(res), std::end(res),
            [&](const std::set<K>& lhs, const std::set<K>& rhs) {
                return lhs.size() < rhs.size();
            });
        return res;
    }

    template <typename K, typename V>
    inline void DAGGraph<K, V>::DFS(const K& k, std::unordered_set<K>* visited,
        std::set<K>* connected_components) const {
        if (visited->count(k)) {
            return;
        }
        visited->emplace(k);
        connected_components->emplace(k);
        if (!bucket_.at(k).in.empty()) {
            for (DAGNode<K, V>* v : bucket_.at(k).in) {
                DFS(v->k, visited, connected_components);
            }
        }
        if (!bucket_.at(k).out.empty()) {
            for (DAGNode<K, V>* v : bucket_.at(k).out) {
                DFS(v->k, visited, connected_components);
            }
        }
    }

    template <typename K, typename V>
    inline std::vector<K> DAGGraph<K, V>::TopologicalSequence(
        const std::set<K>& connected_components, bool start_from_head) const {
        std::map<K, std::vector<K>> adjacency_list;
        std::map<K, int32_t> in_degree;

        for (const K& key : connected_components) {
            if (!in_degree.count(key)) {
                in_degree.emplace(key, 0);
            }
            const std::set<DAGNode<K, V>*>& nodes =
                start_from_head ? bucket_.at(key).out : bucket_.at(key).in;
            for (DAGNode<K, V>* v : nodes) {
                adjacency_list[key].emplace_back(v->k);
                ++in_degree[v->k];
            }
        }

        std::queue<K> q;
        for (auto& x : in_degree) {
            if (x.second == 0) {
                q.emplace(x.first);
            }
        }

        std::vector<K> res;
        while (!q.empty()) {
            const K key = q.front();
            q.pop();
            res.emplace_back(key);
            for (const K& k : adjacency_list[key]) {
                if (--in_degree.at(k) == 0) {
                    q.emplace(k);
                }
            }
        }

        assert(res.size() == connected_components.size());  // graph is DAG
        return res;
    }

}  // namespace jc

namespace jc::test {

    class MockPipelineEngine {
    public:
        void Start() {}
        void Stop() {}
        void Destroy() {}
    };

    void test() {
        DAGGraph<int, std::unique_ptr<MockPipelineEngine>> d;
        // Make Direct Acyclic Graph:
        //    0    6      11  13
        //   / \   |      |
        //  1   3  7  8   12
        //  | x |      \ /
        //  2   4       9
        //   \ /        |
        //    5         10
        // Traverse each child graph in order whose size smaller

        // Start Order:
        // 13
        // 6 -> 7
        // 8 -> 11 -> 12 -> 9 -> 10
        // 0 -> 1 -> 3 -> 2 -> 4 -> 5
        // Stop Order:
        // 13
        // 7 -> 6
        // 10 -> 9 -> 8 -> 12 -> 11
        // 5 -> 2 -> 4 -> 1 -> 3 -> 0

        constexpr int nodes_count = 14;
        for (int i = 0; i < nodes_count; ++i) {
            d[i].reset(new MockPipelineEngine);
        }
        assert(d.AddEdge(0, 1));
        assert(d.AddEdge(0, 3));
        assert(d.AddEdge(1, 2));
        assert(d.AddEdge(3, 4));
        assert(d.AddEdge(1, 4));
        assert(d.AddEdge(3, 2));
        assert(d.AddEdge(2, 5));
        assert(d.AddEdge(4, 5));
        assert(d.AddEdge(6, 7));
        assert(d.AddEdge(8, 9));
        assert(d.AddEdge(9, 10));
        assert(d.AddEdge(11, 12));
        assert(d.AddEdge(12, 9));

        assert(d.Size() == nodes_count);

        for (int i = 0; i < nodes_count; ++i) {
            assert(d.Exist(i));
        }

        assert(!d.AddEdge(1, 0));
        assert(!d.AddEdge(2, 0));
        assert(!d.AddEdge(4, 0));
        assert(!d.AddEdge(7, 6));
        assert(!d.AddEdge(10, 11));
        assert(!d.AddEdge(13, 13));
        assert(!d.AddEdge(13, 14));

        constexpr bool start_from_head = true;
        {
            std::vector<int> v;
            std::vector<int> start_order{ 13, 6, 7, 8, 11, 12, 9, 10, 0, 1, 3, 2, 4, 5 };
            std::vector<int> start_order2{ 13, 6, 7, 8, 11, 12, 9, 10, 0, 3, 1, 4, 2, 5 };
            d.Walk(
                [&](int key, const std::unique_ptr<MockPipelineEngine>& pipeline) {
                    pipeline->Start();
                    v.emplace_back(key);
                },
                start_from_head);
            assert(v == start_order || v == start_order2);
        }

        {
            std::vector<int> v;
            std::vector<int> stop_order{ 13, 7, 6, 10, 9, 8, 12, 11, 5, 2, 4, 1, 3, 0 };
            std::vector<int> stop_order2{ 13, 7, 6, 10, 9, 12, 8, 11, 5, 2, 4, 1, 3, 0 };
            d.Walk(
                [&](int key, const std::unique_ptr<MockPipelineEngine>& pipeline) {
                    pipeline->Stop();
                    v.emplace_back(key);
                },
                !start_from_head);
            assert(v == stop_order || v == stop_order2
            );
        }

        {
            std::vector<int> v;
            std::vector<int> heads_order{ 13, 6, 8, 11, 0 };
            d.WalkHeads(
                [&](int key, const std::unique_ptr<MockPipelineEngine>& pipeline) {
                    pipeline->Destroy();
                    v.emplace_back(key);
                });
            assert(v == heads_order);
        }

        {
            std::vector<int> v;
            std::vector<int> tails_order{ 13, 7, 10, 5 };
            d.WalkTails(
                [&](int key, const std::unique_ptr<MockPipelineEngine>& pipeline) {
                    pipeline->Destroy();
                    v.emplace_back(key);
                });
            assert(v == tails_order);
        }

        {
            std::vector<int> test_sequence{ 13, 6, 7, 0,  1,  3, 4,
                                           2,  5, 8, 11, 12, 9, 10 };

            std::unordered_set<int> heads{ 0, 6, 8, 11, 13 };
            assert(d.NextKeys() == heads);

            std::vector<std::unordered_set<int>> next_keys{
                {}, {7}, {}, {1, 3}, {}, {2, 4}, {}, {5}, {}, {}, {12}, {9}, {10}, {},
            };

            assert(test_sequence.size() == nodes_count);
            assert(next_keys.size() == nodes_count);
            for (int i = 0; i < nodes_count; ++i) {
                assert(d.NextKeys(test_sequence[i]) == next_keys[i]);
            }
        }

        d.Clear();
        assert(d.Size() == 0);
        for (int i = 0; i < nodes_count; ++i) {
            assert(!d.Exist(i));
        }
    }

}  // namespace jc::test

//int main() { jc::test::test(); }

效果