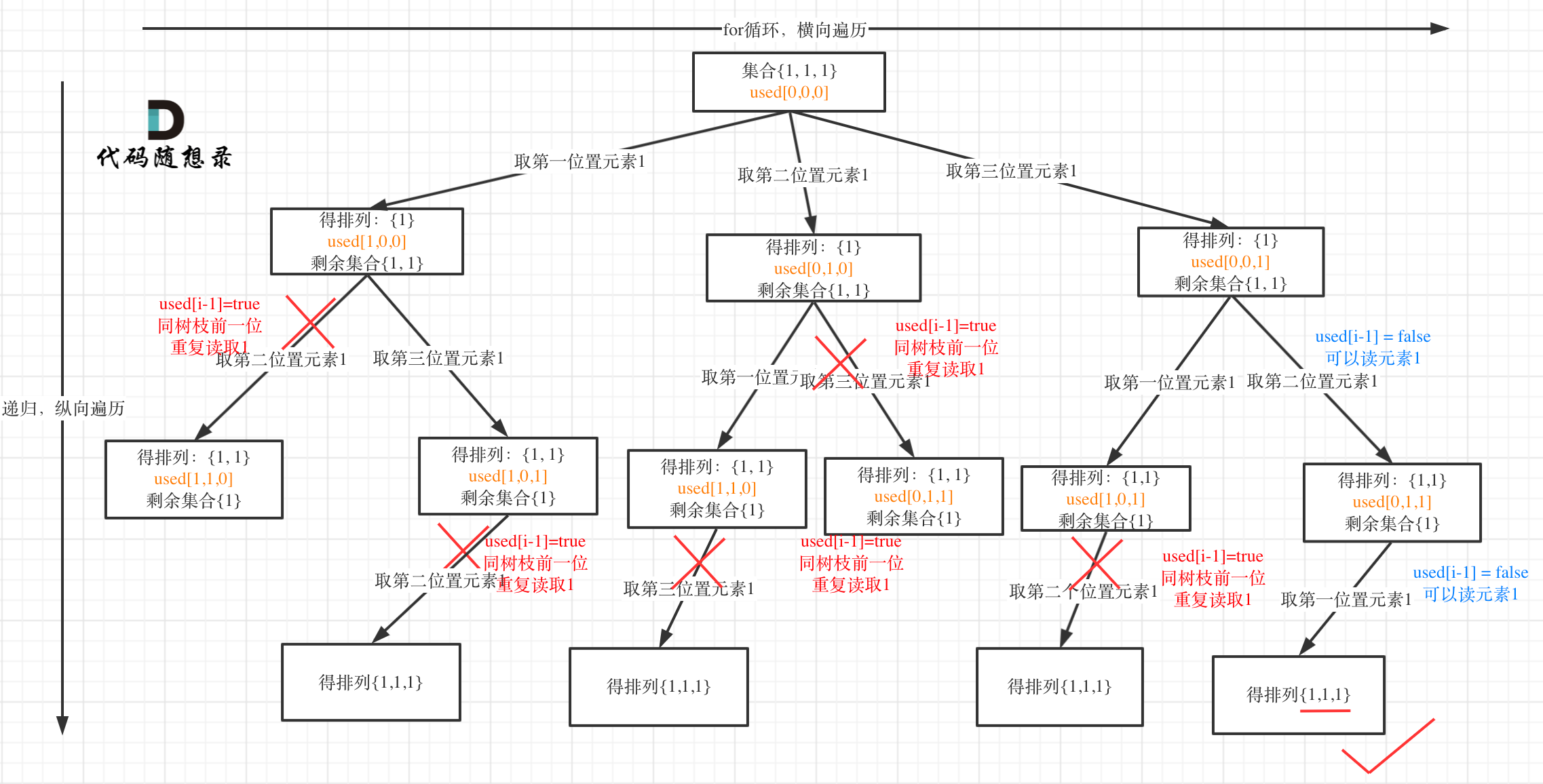
排序补充之快排的三路划分法

快排性能的关键点分析：

决定快排性能的关键点是每次单趟排序后，key对数组的分割，如果每次选key基本⼆分居中，那么快 排的递归树就是颗均匀的满⼆叉树，性能最佳。但是实践中虽然不可能每次都是⼆分居中，但是性能 也还是可控的。但是如果出现每次选到最⼩值/最⼤值，划分为0个和N-1的⼦问题时，时间复杂度为 O(N^2)，数组序列有序时就会出现这样的问题，我们前⾯已经⽤三数取中或者随机选key解决了这个问 题，也就是说我们解决了绝⼤多数的问题，但是现在还是有⼀些场景没解决(数组中有⼤量重复数据 时)，类似⼀下代码。

// 数组中有多个跟key相等的值
int a[] = { 6,1,7,6,6,6,4,9 };
int a[] = { 3,2,3,3,3,3,2,3 };
// 数组中全是相同的值
int a[] = { 2,2,2,2,2,2,2,2 };

三路划分算法思想讲解：

当⾯对有⼤量跟key相同的值时，三路划分的核⼼思想有点类似hoare的左右指针和lomuto的前后指针 的结合。核⼼思想是把数组中的数据分为三段【⽐key⼩的值】 【跟key相等的值】【⽐key⼤的 值】，所以叫做三路划分算法。

1. key默认取left位置的值。
2. left指向区间最左边，right指向区间最后边，cur指向left+1位置。
3. cur遇到⽐key⼩的值后跟left位置交换，换到左边，left++，cur++。
4. cur遇到⽐key⼤的值后跟right位置交换，换到右边，right–。
5. cur遇到跟key相等的值后，cur++。
6. 直到cur > right结束

代码如下：

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<string.h>
void PrintArray(int* a, int n)
{
 for (int i = 0; i < n; ++i)
 {
 printf("%d ", a[i]);
 }
 printf("\n");
}
void Swap(int* p1, int* p2)
{
 int tmp = *p1;
 *p1 = *p2;
 *p2 = tmp;
}

typedef struct
{
 int leftKeyi;
 int rightKeyi;
}KeyWayIndex;
// 三路划分
KeyWayIndex PartSort3Way(int* a, int left, int right)
{
 int key = a[left];
 // left和right指向就是跟key相等的区间
 // [开始, left-1][left, right][right+1, 结束]
 int cur = left + 1;
 while (cur <= right)
 {
 // 1、cur遇到⽐key⼩，⼩的换到左边，同时把key换到中间位置
 // 2、cur遇到⽐key⼤，⼤的换到右边
if (a[cur] < key)
 {
 Swap(&a[cur], &a[left]);
 ++cur;
 ++left;
 }
 else if (a[cur] > key)
 {
 Swap(&a[cur], &a[right]);
 --right;
 }
 else
 {
 ++cur;
 }
 }
 KeyWayIndex kwi;
 kwi.leftKeyi = left;
 kwi.rightKeyi = right;
 return kwi;
}