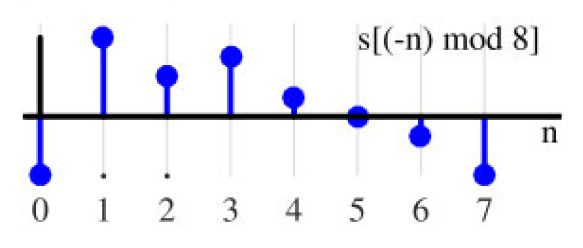
已知空间上的某一个点P在坐标系1下的位置为 P1(1,2,3),需要求出P在三维空间坐标系0之间的相对关系,其中坐标系1是相对于坐标系0绕着x轴旋转60度后转化。示意如下图

程序设计
- 定义P点在坐标系1下的位置
array = np.array([1,2,3])
# [1 2 3]
- 定义坐标系1和坐标系0之间的旋转矩阵
PI = 3.14
angle = 60/360*PI
transforat_array = np.array([[1,0,0],
[0,math.cos(angle),math.sin(angle)],
[0,-math.sin(angle),math.cos(angle)]])
# [[ 1. 0. 0. ]
# [ 0. 0.86615809 0.4997701 ]
# [ 0. -0.4997701 0.86615809]]
- 得到转换结果
d = np.dot(array,transforat_array)
# [1. 0.23300588 3.59801449]
整体程序
import math
import numpy as np
PI = 3.14
array = np.array([1,2,3])
angle = 60/360*PI
print(angle)
transforat_array = np.array([[1,0,0],
[0,math.cos(angle),math.sin(angle)],
[0,-math.sin(angle),math.cos(angle)]])
print(array)
print(transforat_array)
d = np.dot(array,transforat_array)
print(d)
使用ROS 的RVIZ进行查看验证
按照顺序打开和输入指令,不同的的指令需要开启不同的终端执行
roscore
rosrun tf2_ros static_transform_publisher 1 2 3 0 0 0 /base_1 /p
rosrun tf2_ros static_transform_publisher 0 0 0 0 0 0.523333 /base_0 /base_1
rosrun rviz rviz
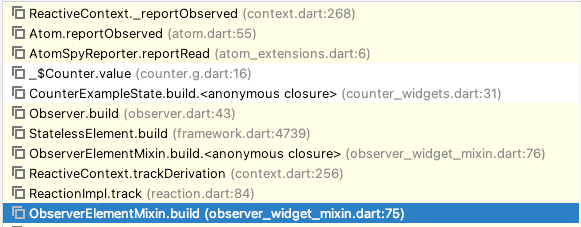
讲话Fixed Frame选择为base_0,表示观察的基坐标,然后就可以查看P点和他之间的相对位置关系,可以从中第二个方框看出ROS计算得到的旋转结果和之前python程序计算出来的结果相同。

在测试的Demo当中,使用的还是静态的发布关系,一般在机械臂上面各个关节关节之间的关系一般会保持静止,变动的是末端执行机构和目标物体之间的相对位置姿态,后续就可以程序来找出机械臂末端的执行机构需要运动到达目标物体的角度和路线了。