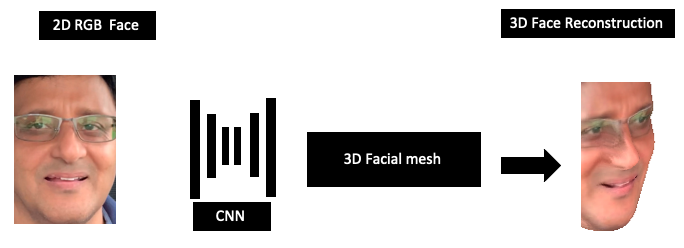
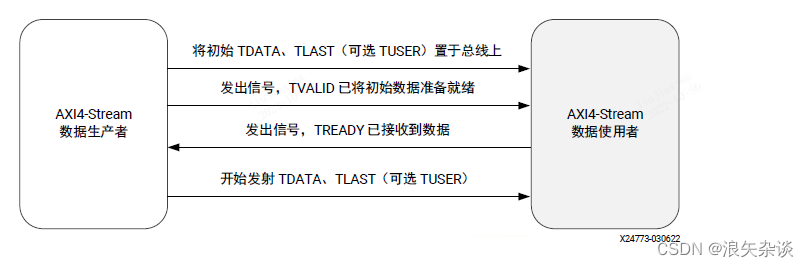
凸集和凸函数

 

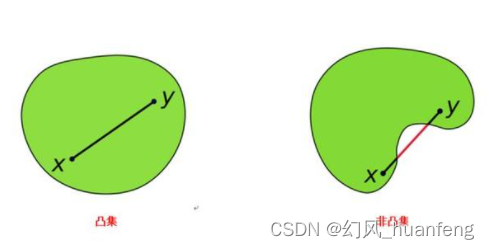
在点集拓扑学与欧几里得空间中，凸集是一个点集，其中每两点之间的直线上的点都落在该点集中。如下所示：

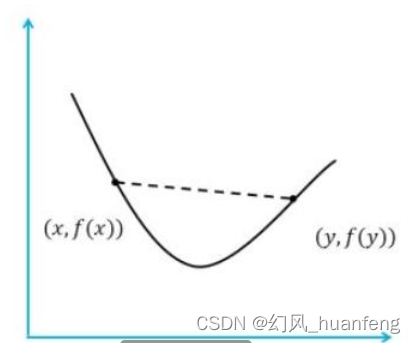
函数任意两点(x,f(x))和(y,f(y))连线上的值大于(x,y)区间内任意一点m的值f(m)，那么这个函数就是一个凸函数：

 

超平面分离定理

空间中存在两类样本，是否一定存在分割超平面能够将两类分割开？

这里存在一个超平面分离定理：它的意思是这样的，两个不相交的凸集，一定存在一个超平面能将其分开。若在两个凸集中有：

 

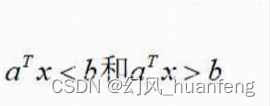
则这两个凸集肯定能够严格分开。所以根据超平面分离定理可知，对于二分类问题而言，必然存在一个超平面（即分割超平面）能够将两类样本严格分开。而SVM求得的超平面就是这两个凸包上距离最短的两点连线的中垂线，也就是凸优化理论中的超平面分离定理中二维情况中所阐释的分类超平面。

凸优化

凸优化问题࿱