文章目录
- 题目
- 任务
- 做题解析
- 第一问
- 第三问
- 第四问
- 第一个预测
- 第二个预测
- 第五问
- 关键技术摘要
- 代码文件下载
题目
制造业是国民经济的主体,近十年来,嫦娥探月、祝融探火、北斗组网,一大批重大标志性创新成果引领中国制造业不断攀上新高度。作为制造业的核心,机械设备在工业生产的各个环节都扮演着不可或缺的重要角色。但是,在机械设备运转过程中会产生不可避免的磨损、老化等问题,随着损耗的增加,会导致各种故障的发生,影响生产质量和效率。
实际生产中,若能根据机械设备的使用情况,提前预测潜在的故障风险,精准地进行检修维护,维持机械设备稳定运转,不但能够确保整体工业环境运行具备稳定性,也能切实帮助企业提高经济效益。
某企业机械设备的使用情况及故障发生情况数据见“train data.xlsx”,用于设备故障预测及故障主要相关因素的探究。数据包含 9000 行,每一行数据记录了机械设备对应的运转及故障发生情况记录。因机械设备在使用环境以及工作强度上存在较大差异,其所需的维护频率和检修问题也通常有所不同。
数据提供了实际生产中常见的机械设备使用环境和工作强度等指标,包含不同设备所处厂房的室温(单位为开尔文K),其工作时的机器温度(单位为开尔文K)、转速(单位为每分钟的旋转次数rpm)、扭矩(单位为牛米Nm)及机器运转时长(单位为分钟min)。除此之外,还提供了机械设备的统一规范代码、质量等级及在该企业中的机器编号,其中质量等级分为高、中、低(H\M\L)三个等级。对于机械设备的故障情况,数据提供了两列数据描述——“是否发生故障” 和“具体故障类别”。其中“是否发生故障”取值为 0/1,0 代表设备正常运转,1 代
表设备发生故障;“具体故障类别”包含 6 种情况,分别是NORMAL、TWF、HDF、PWF、OSF、RNF,其中,NORMAL代表设别正常运转(与是否发生故障”为 0相对应),其余代码代表的是发生故障的类别,包含 5 种,其中TWF代表磨损故障,HDF代表散热故障,PWF代表电力故障,OSF代表过载故障,RNF代表其他故障。
任务
基于赛题提供的数据,自主查阅资料,选择合适的方法完成如下任务:
任务 1:观察数据“train data.xlsx”,自主进行数据预处理,选择合适的指标用于机械设备故障的预测并说明原因。
任务 2:设计开发模型用于判别机械设备是否发生故障,自主选取评价方式和评价指标评估模型表现。
任 务 3 : 设 计 开 发 模 型 用 于 判 别 机 械 设 备 发 生 故 障 的 具 体 类 别(TWF/HDF/PWF/OSF/RNF),自主选取评价方式和评价指标评估模型表现
任务 4:利用任务 2 和任务 3 开发的模型预测“forecast.xlsx”中是否发生故障以及故障类别。数据“forecast.xlsx”。与数据“train data.xlsx”格式类似,要求在“forecast.xlsx”第 8 列说明设备是否发生故障(0 或 1),在第 9 列标识出具体的故障类型(TWF/HDF/PWF/OSF/RNF)
任务 5:探究每类故障(TWF/HDF/PWF/OSF/RNF)的主要成因,找出与其相关的特征属性,进行量化分析,挖掘可能存在的模式/规则。
做题解析
读完题目,其实我想到了今年长三角数学建模中的齿轮箱故障监测,基本很像。难度不大,注意一些细节,随便拿二等,论文好好优化就一等奖了。
第一问
观察数据“train data.xlsx”,自主进行数据预处理,选择合适的指标用于机械设备故障的预测并说明原因。
首先读取数据:
import pandas as pd
data=pd.read_excel('train data.xlsx')
data.head(10)
得到如下:
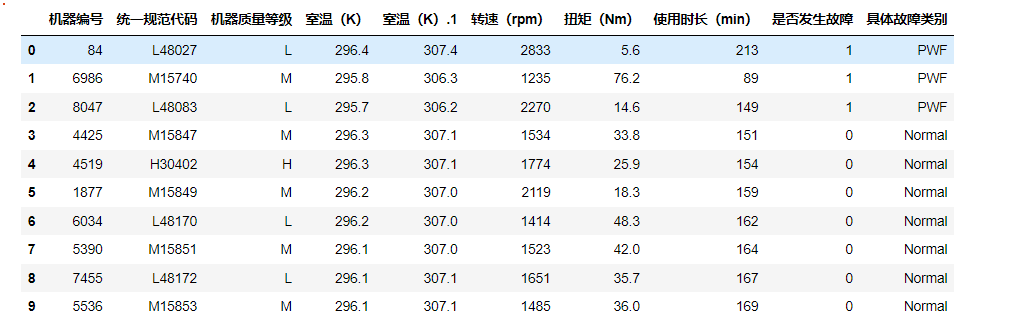
查看数据基本信息:
data.info()
如下:
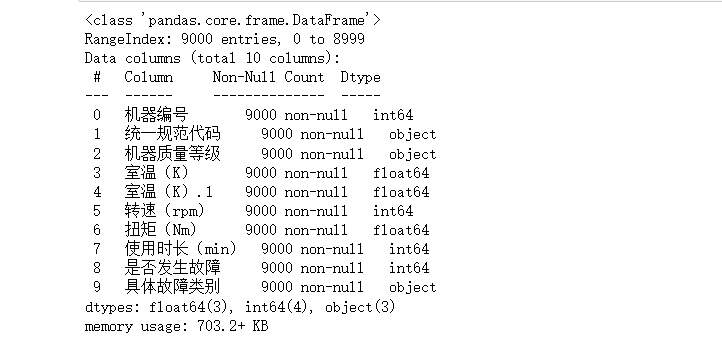
看起来是没有缺失值的,再用isnull来查看一下是否又缺失值:
data.isnull().sum()
如下:

可以看到数据肯定是没有缺失值的。
查看数据有哪些特征:
data.columns
得到如下:
Index(['机器编号', '统一规范代码', '机器质量等级', '室温(K)', '室温(K).1', '转速(rpm)', '扭矩(Nm)',
'使用时长(min)', '是否发生故障', '具体故障类别'],
dtype='object')
很明显,与机器真正相关的特征中,‘机器编号’, '统一规范代码’这两个是无关的,所以可以删除这两个特征。第一问和第二问都属有一个目标,预测是否发生预测,因此在第一问和第二问中,“具体故障类别”也不是我们需要用的指标。所以也要删除。
data2=data.drop(['机器编号', '统一规范代码','具体故障类别'],axis=1)
data2.head()
得到新的数据如下:
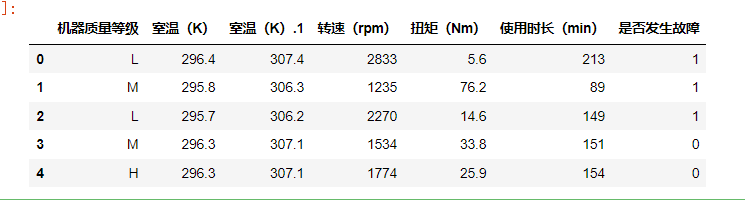
继续回到目标:数据预处理,并选择合适的指标用于机械设备故障的预测。指标我们已经选取好了,那就是:“机器质量等级 室温(K) 室温(K).1 转速(rpm) 扭矩(Nm) 使用时长(min)”
接下来就说做数据预处理了,我们可以看到:机器质量等级,这个特征属于离散变量而且是字符型,所以需要进行编码处理。先查看这一列有多少等级:
data2['机器质量等级'].unique()
如下,只有三个等级:
array(['L', 'M', 'H'], dtype=object)
大多数人可能会想到通过映射的方式对它们进行编码:
mapping = {
'L': 3,
'M': 2,
'H': 1}
data2['机器质量等级'] =data2['机器质量等级'].map(mapping)
data2.head()
如下:
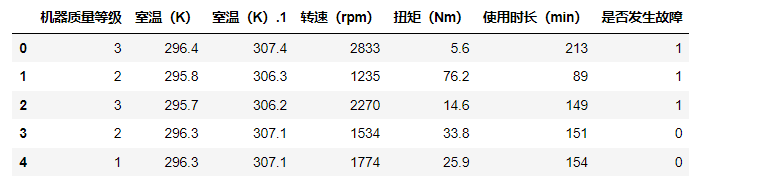
这样进行映射也不是不可以,只是这样的方式效果不是最好的,因此我建议使用独热编码,独热编码很适合用来解决类别型数据的离散值问题。
data3=pd.get_dummies(data2,columns=['机器质量等级'])
data3.head()
得到如下:

查看类的分布:
df1=data3['是否发生故障'].value_counts()
df1
如下:
0 8697
1 303
Name: 是否发生故障, dtype: int64
可以看出有明显的类不平衡问题,等会需要解决它。提取自变量和因变量:
X = data3.drop('是否发生故障',axis=1)# 特征
y = data3['是否发生故障'] # 目标变量
X
如下:
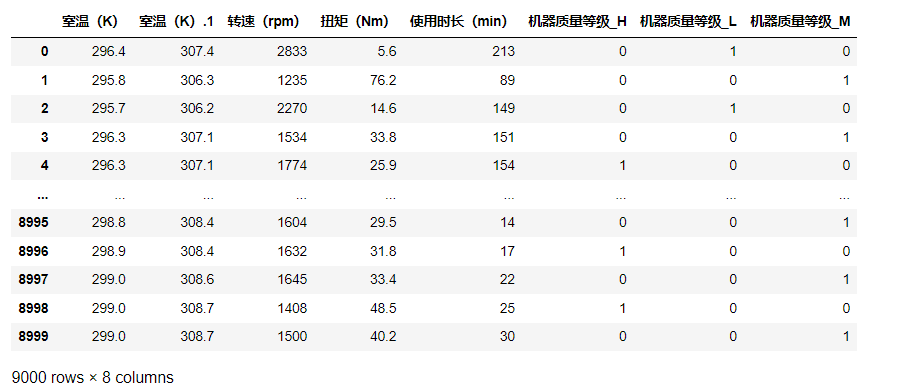
执行欠采样技术,解决类不平衡的问题:
# 欠采样
from collections import Counter
from imblearn.under_sampling import ClusterCentroids
cc = ClusterCentroids(random_state=2022)
X_resampled, y_resampled = cc.fit_resample(X, y)
print(sorted(Counter(y_resampled).items()))
如下:
[(0, 303), (1, 303)]
分割数据:
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X_resampled,y_resampled,test_size=0.2,random_state=100)
使用逻辑回归模型:
# 导入模型
from sklearn.linear_model import LogisticRegression
# 初始化模型,使用默认参数
logreg = LogisticRegression()
# 用数据训练模型
logreg.fit(X_train,y_train)
# 使用模型预测
y_pred=logreg.predict(X_test)
y_pred
评估:
from sklearn import metrics
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
print("Precision:",metrics.precision_score(y_test, y_pred))
print("Recall:",metrics.recall_score(y_test, y_pred))
如下:
Accuracy: 0.9426229508196722
Precision: 0.9242424242424242
Recall: 0.9682539682539683
准确率97%挺高了吧,还可以了。为了提升准确率,还可以对数据做归一化,自行尝试。
这里我再用决策树进行尝试:
from sklearn.tree import DecisionTreeClassifier # 导入决策树
# 选择基尼系数作为判断标准,树深度为3
clf_gini = DecisionTreeClassifier(criterion='gini', max_depth=3, random_state=0)
clf_gini.fit(X_train, y_train) #训练模型
y_pred_gini = clf_gini.predict(X_test) # 预测模型
y_pred_gini[0:5] # 预测前五个结果
如下:
array([0, 0, 0, 0, 0], dtype=int64)
接着做评估:
from sklearn import metrics
print("Accuracy:",metrics.accuracy_score(y_test, y_pred_gini))
print("Precision:",metrics.precision_score(y_test, y_pred_gini))
print("Recall:",metrics.recall_score(y_test, y_pred_gini))
如下:
Accuracy: 0.9716666666666667
Precision: 0.8260869565217391
Recall: 0.2878787878787879
可视化一下:
import matplotlib.pyplot as plt
plt.figure(figsize=(12,8))
from sklearn import tree
tree.plot_tree(clf_gini.fit(X_train, y_train))
如下:
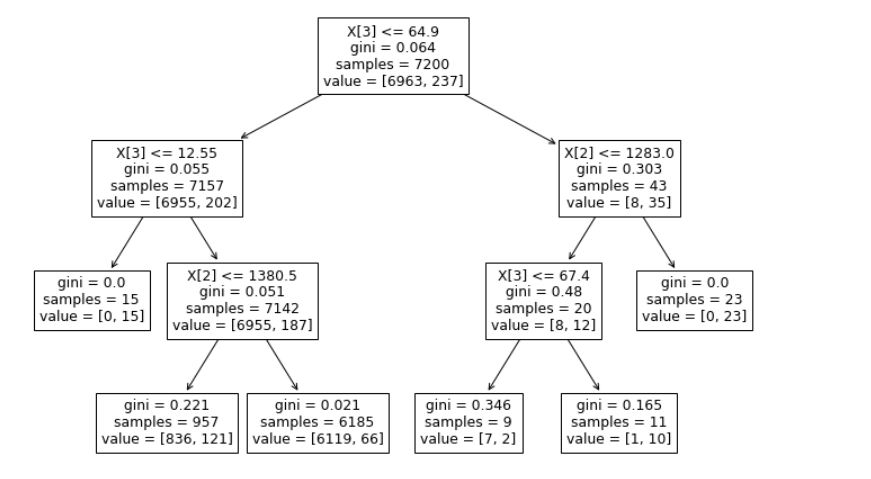
可视化混淆矩阵:
# 可视化混淆矩阵
from sklearn.metrics import plot_confusion_matrix
plot_confusion_matrix(clf_gini , X_test, y_test)
plt.show()
如下:
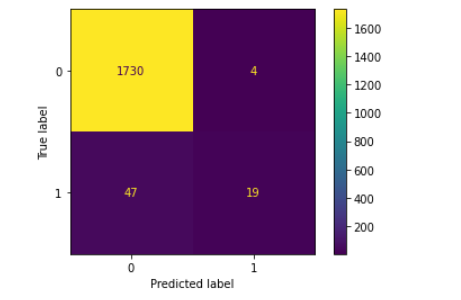
这个结果好吗?不,我们来寻优找到最佳参数。
1)确定max_depth最优
## 确定最佳深度
import numpy as np
from sklearn.tree import DecisionTreeClassifier # 导入决策树
score_all=[]
# range(start, stop[, step])
for i in range(1,100,1):
# 选择基尼系数作为判断标准,树深度为3
clf_gini = DecisionTreeClassifier(criterion='gini', max_depth=i, random_state=0)
clf_gini.fit(X_train, y_train) #训练模型
y_pred_gini = clf_gini.predict(X_test) # 预测模型
y_pred_gini[0:5] # 预测前五个结果
from sklearn.metrics import accuracy_score
acc=accuracy_score(y_test, y_pred_gini)
# print(acc)
score_all.append([i,acc])
ScoreAll = np.array(score_all)
max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] #找出最高得分对应的索引
print("最优参数以及最高得分:",ScoreAll[max_score])
plt.figure(figsize=[20,5])
plt.plot(ScoreAll[:,0],ScoreAll[:,1])
plt.show()
如下,我们的树深度为9的时候最佳分数为0.985:
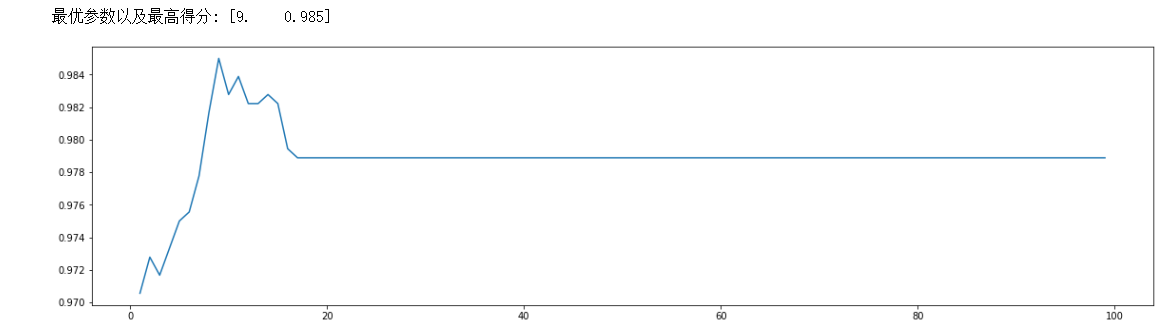
2)确定min_samples_split最优
# 分割内部节点所需的最小样本数
## 确定最佳深度max_depth
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier # 导入决策树
score_all=[]
# range(start, stop[, step])
# 带入最佳深度后,再遍历2到20的内部最小样本数
for i in range(2,20,1):
# 选择基尼系数作为判断标准,树深度为3
clf_gini = DecisionTreeClassifier(criterion='gini', max_depth=9, min_samples_split=i,random_state=0)
clf_gini.fit(X_train, y_train) #训练模型
y_pred_gini = clf_gini.predict(X_test) # 预测模型
y_pred_gini[0:5] # 预测前五个结果
from sklearn.metrics import accuracy_score
acc=accuracy_score(y_test, y_pred_gini)
# print(acc)
score_all.append([i,acc])
ScoreAll = np.array(score_all)
max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] #找出最高得分对应的索引
print("最优参数以及最高得分:",ScoreAll[max_score])
plt.figure(figsize=[20,5])
plt.plot(ScoreAll[:,0],ScoreAll[:,1])
plt.show()
# 结果显示默认的2就是最佳
如下,可以看到内部节点所需的最小样本数为5的时候,最佳准确度为 0.98611111了:
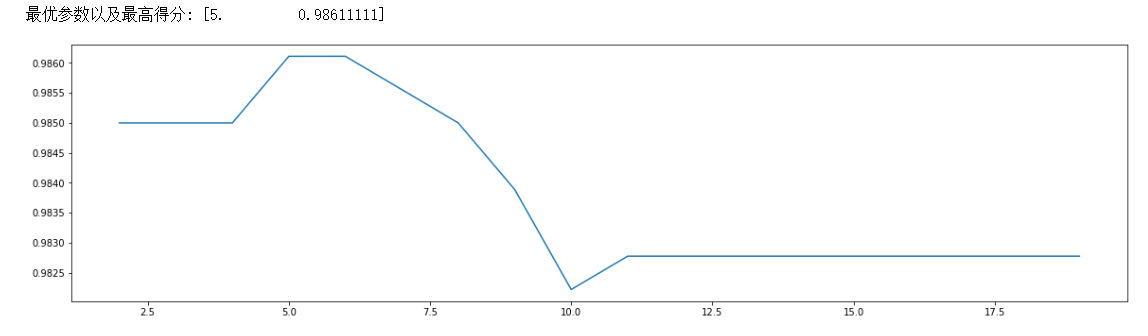
3)确定min_samples_leaf参数
# 确定
# 分割内部节点所需的最小样本数min_samples_split
## 确定最佳深度max_depth
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier # 导入决策树
score_all=[]
# range(start, stop[, step])
# 带入最佳深度=12,min_samples_split=2,遍历min_samples_leaf = i
for i in range(1,20,1):
# 选择基尼系数作为判断标准,树深度为3
clf_gini = DecisionTreeClassifier(criterion='gini', max_depth=9, min_samples_split=5,min_samples_leaf = i,random_state=0)
clf_gini.fit(X_train, y_train) #训练模型
y_pred_gini = clf_gini.predict(X_test) # 预测模型
y_pred_gini[0:5] # 预测前五个结果
from sklearn.metrics import accuracy_score
acc=accuracy_score(y_test, y_pred_gini)
score_all.append([i,acc])
ScoreAll = np.array(score_all)
max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] #找出最高得分对应的索引
print("最优参数以及最高得分:",ScoreAll[max_score])
plt.figure(figsize=[20,5])
plt.plot(ScoreAll[:,0],ScoreAll[:,1])
plt.show()
# 最佳参数还是2
如下,min_samples_leaf最佳值为2,此时准确度为0.98666667:
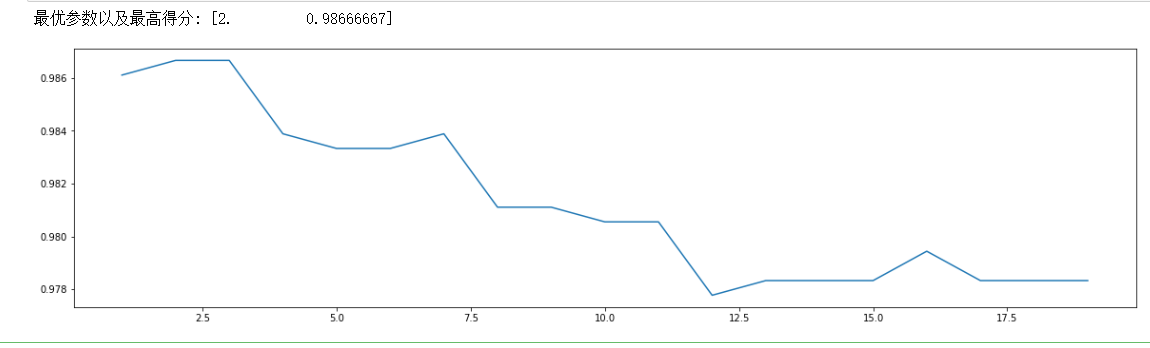
根据我们前边的一系列操作,我们确定因为max_depth在9附近,min_samples_split在5附近,min_samples_leaf在2附近是最优参数,所以我们分别在这个附近利用网格搜索得到最优参数。因为要涉及到三个参数联调,这里就要用到网格搜索函数。代码如下:
# 网格搜索确定内联最佳
from sklearn.model_selection import GridSearchCV
param_grid = {
'max_depth':np.arange(6, 12),
'min_samples_leaf':np.arange(3, 7),
'min_samples_split':np.arange(1, 4)}
rfc = DecisionTreeClassifier(random_state=66)
GS = GridSearchCV(rfc,param_grid,cv=10)
GS.fit(X_train, y_train)
print(GS.best_params_)
print(GS.best_score_)
#这里三个参数和我们前边所暂定的参数都不一样。证明三者之间确实是相互影响的。最终确定还是选取开始的三个。
如下:
{'max_depth': 6, 'min_samples_leaf': 5, 'min_samples_split': 2}
0.9834608843537413
从而得到最佳参数:‘max_depth’: 6, ‘min_samples_leaf’: 5, ‘min_samples_split’: 2},此时准确率为0.9834608843537413
其余还要很多模型,大家可以去尝试。
第三问
设 计 开 发 模 型 用 于 判 别 机 械 设 备 发 生 故 障 的 具 体 类 别
(TWF/HDF/PWF/OSF/RNF),自主选取评价方式和评价指标评估模型表现
第三问跟第一二问不一样了,这里是个多分类问题。所以重新建立一个文件,读取数据,同时还需要删除是否发生故障,因为我认为这个不叫作特征了:
import pandas as pd
data=pd.read_excel('train data.xlsx')
data2=data.drop(['机器编号', '统一规范代码','是否发生故障'],axis=1)
data2.head()
如下:
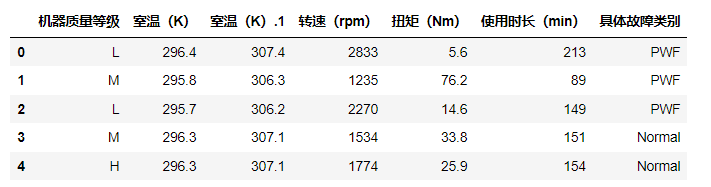
查看具体工作类别有哪些:
data2['具体故障类别'].unique()
如下:
array(['PWF', 'Normal', 'OSF', 'TWF', 'RNF', 'HDF'], dtype=object)
查看质量等级有哪些:
data2['机器质量等级'].unique()
如下:
array(['L', 'M', 'H'], dtype=object)
对质量等级映射编码:
mapping = {
'H': 3,
'M': 2,
'L': 1
}
data2['机器质量等级'] =data2['机器质量等级'].map(mapping)
data2.head()
如下:
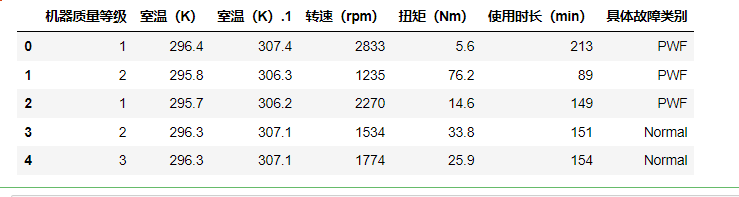
查看每个故障类型数量:
df1=data2['具体故障类别'].value_counts()
df1
如下:
Normal 8699
HDF 95
OSF 85
PWF 74
TWF 41
RNF 6
Name: 具体故障类别, dtype: int64
可以看到类型6个,即Normal数量很多,可视化一下更明显:
df1.plot.barh()
如下:
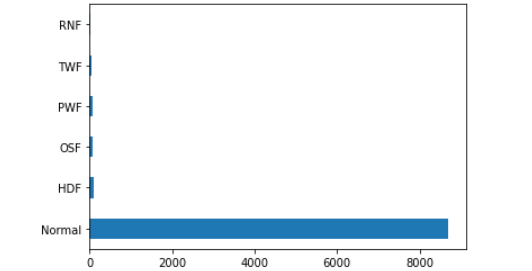
为了便于处理,我们对目标变量直接进映射编码即可:
mapping = {
'PWF': 6,
'Normal': 5,
'OSF': 4,
'TWF':3,
'RNF':2,
'HDF': 1
}
data2['具体故障类别'] =data2['具体故障类别'].map(mapping)
data2.head()
如下:

接着开始建立模型,我们首先提取自变量因变量:
from sklearn.model_selection import train_test_split
x=data2.drop(columns='具体故障类别')
y=data2['具体故障类别']
执行合成少数过采样技术 (SMOTE),解决适当的不平衡问题:
from collections import Counter
from imblearn.over_sampling import SMOTE
smote_technique = SMOTE(sampling_strategy='minority')
X_smt, y_smt = smote_technique.fit_resample(x, y)
print(sorted(Counter(y_smt).items()))
如下:
[(1, 95), (2, 8699), (3, 41), (4, 85), (5, 8699), (6, 74)]
分割训练集和测试集:
X_train, X_test, y_train, y_test = train_test_split(X_smt, y_smt, test_size=0.2, random_state=1)
X_train
如下:
建立xgboost模型:
#分类器使用 xgboost
from xgboost import XGBClassifier
model = XGBClassifier()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
y_pred
评估:
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))
如下:
precision recall f1-score support
1 0.95 0.76 0.84 25
2 0.99 1.00 1.00 1749
3 1.00 0.11 0.20 9
4 1.00 0.83 0.91 18
5 0.99 0.99 0.99 1718
6 0.93 0.65 0.76 20
accuracy 0.99 3539
macro avg 0.98 0.72 0.78 3539
weighted avg 0.99 0.99 0.99 3539
第四问
分别把第二问和第三问的模型带进去,分别预测两列数据即可。(看大家都不会,我再补充点)
第一个预测
第一问的决策树模型保存到本地:
import pickle
pickle.dump(GS, open('model.pkl', 'wb'))
接着导入需要预测的数据,做相同的删除:
# 读取需要预测的数据
yu=pd.read_excel('forecast.xlsx')
yu2=yu.drop(['机器编号', '统一规范代码'],axis=1)
yu2.head()
如下:
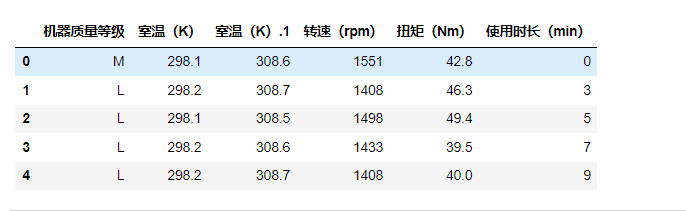
同样对需要预测的数据编码:
yu3=pd.get_dummies(yu2,columns=['机器质量等级'])
yu3.head()
如下:
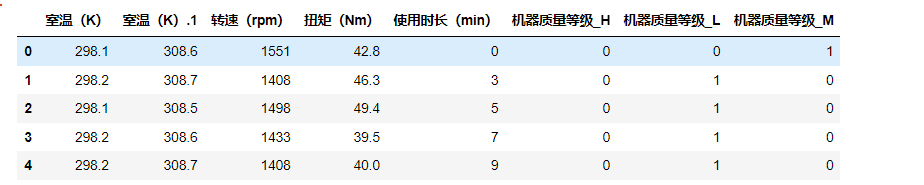
调用决策树模型预测:
pickled_model = pickle.load(open('model.pkl', 'rb'))
pre=pickled_model.predict(yu3)
pre
如下:

转换为dataframe:
a = pd.DataFrame(pre,columns=['预测是否发生故障'])
a
如下:

为了便于整理,把预测后的数据添加到原来文件中:
con=pd.concat([yu2, a], axis=1)
con.to_excel('预测1.xlsx')
con
如下:
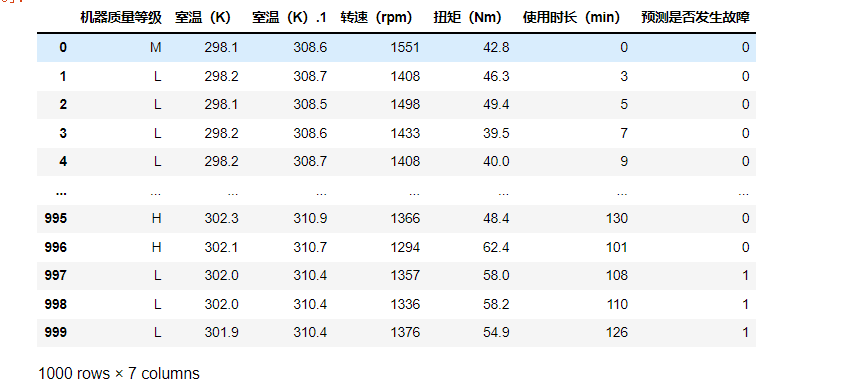
第二个预测
保存第三问的预测类型的模型:
## 保存模型
import pickle
pickle.dump(model, open('lei.pkl', 'wb'))
接着同样方式处理数据,我们只需要在上一个预测后的文件中继续预测即可:
yu=pd.read_excel('预测1.xlsx')
yu.head()
如下:
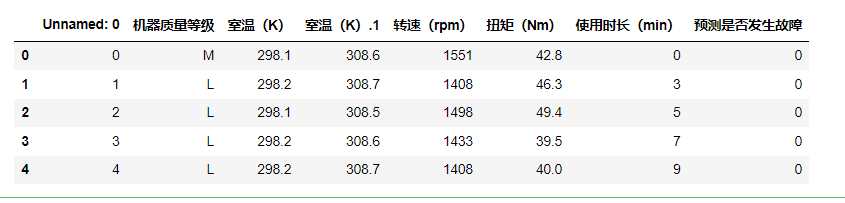
把第一列多余的先删除:
data2=yu.drop(['Unnamed: 0'],axis=1)
data2.head()
如下:
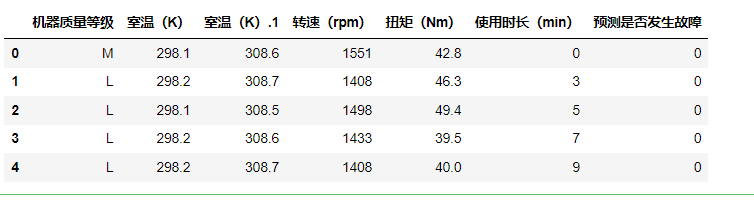
同样方式预处理:
#开始处理数据
data3=yu.drop(['预测是否发生故障'],axis=1) # 原始预测数据
mapping = {
'H': 3,
'M': 2,
'L': 1
}
data3['机器质量等级'] =data3['机器质量等级'].map(mapping)
data3.head()
如下:
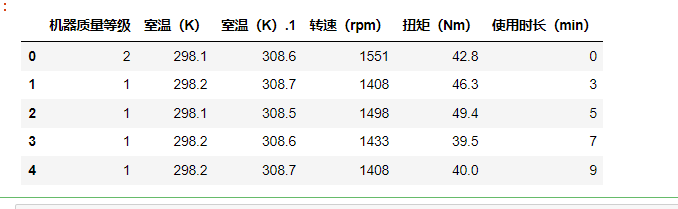
数据处理好了,使用模型预测:
pickled_model = pickle.load(open('lei.pkl', 'rb'))
yu3=pickled_model.predict(data3)
yu3
如下:

转为dataframe格式:
a = pd.DataFrame(yu3,columns=['故障类型'])
a
如下:

合并过去:
con=pd.concat([data2, a], axis=1)
con.to_excel('预测2.xlsx')
con
如下:
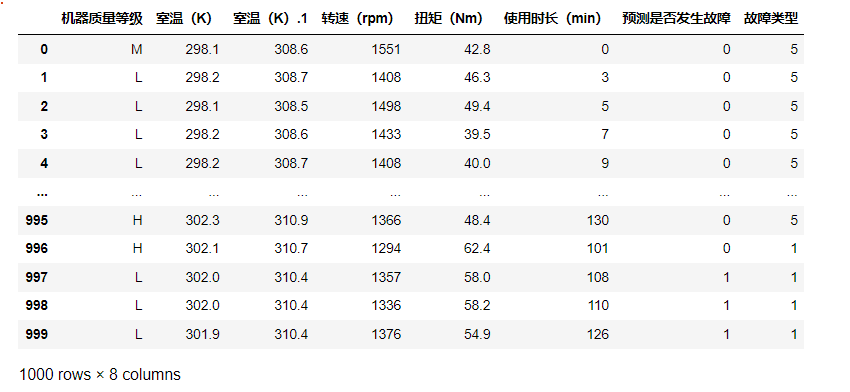
以上就全部预测完了。最后两列数据中,可能有个别数据是没有完全符合,比如997行1对应了5,这个是正常的,个别预测不准没关系。
执行完代码后,你可以看到本地也生成了一个excel文件:预测2.xlsx,就是最终预测结果,如上图一样。
第五问
主要就说探索故障类型和其它特征之间的一个规律关系,可以通过相关性热力图、方差分析等方法,来找到影响最大的特征,以及相关规律,就是主要成因。
更容易看到更新,请看:实时更新,帮你们做了这么多,点击《实时更新》关注一下知乎吧。
关键技术摘要
映射编码、OneHot编码、上采样(SMOTE算法)、欠采样(原型生成算法)、决策树、XGBoost、方差分析
代码文件下载
代码和上面的是一模一样,跳转下载:https://mbd.pub/o/bread/Y5uTlZ9p