1.问题描述
有n种物品,每种物品的单件重量为w[i],价值为v[i]。现有一个容量为V的背包,如何选取物品放入背包,使得背包内物品的总价值最大。
下面是本题中我们使用的例子:
有三个物品,第一个物品的重量为3,价值为4;第二个物品的重量为4,价值为5;第三个物品的重量为5,价值为6。背包的总重量是10,求解背包能放下物品的最大价值。
2.算法描述
2.1 状态转移方程
该背包问题我们用动态规划的思想求解,构造一个二维数组表,以物品为纵坐标,以背包容量为横坐标,记录在不同背包容量下,当前物品摆放与否的最优解。
对第i件物品来说,他的最优解有两种情况:
1.不放第i件物品,那么 dp[ i ][ j ] = dp[ i - 1 ][ j ]
2.放第i件物品。如果选择放这一件物品,那么此时背包需要足够的剩余容量来放置这第i件物品,此时 dp[ i ][ j ] = dp[ i - 1 ][ j - w[i] ] + v[ i ]
我们可以得出此问题的状态转移方程
dp[i][j] = max{dp[ i - 1 ][ j - w[ i ] ] + v[ i ], dp[ i - 1 ][ j ]} 1<=i <=n, w[i] <= j <= V
此时我们的边界条件是:dp[ 0 ][ v ] = 0(0 <= v <= V)
递推求解
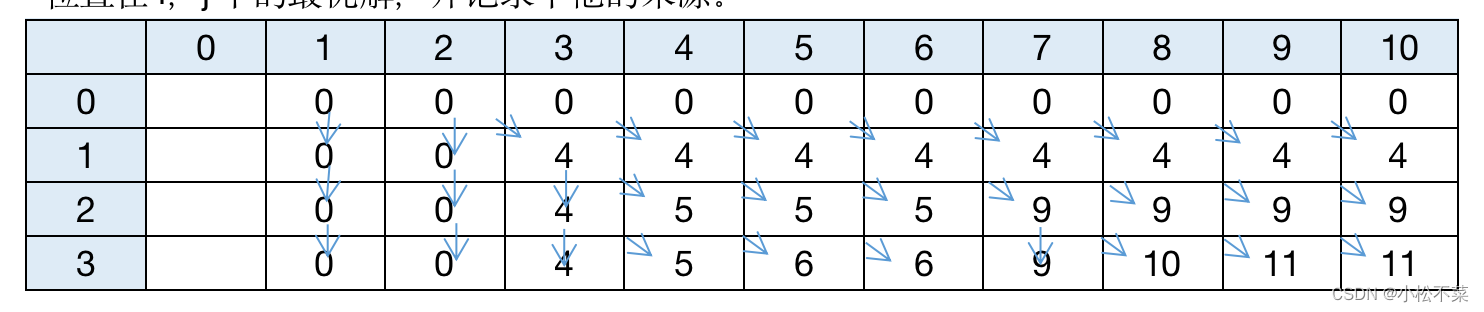
在上一步我们已经得到了状态转移方程,此时我们将该方程运用到构造出的二维表中,得到位置在i,j下的最优解,并记录下他的来源。
实验代码
import copy
if __name__ == "__main__":
weight = [3,4,5]
value = [4,5,6]
capacity = 10
dp = []
temp = []
lastnode = []
for v in range(capacity+1):
temp.append(0)
for u in range(len(weight) + 1):
temp1 = copy.deepcopy(temp)
temp2 = copy.deepcopy(temp)
dp.append(temp1)
lastnode.append(temp2)
for i in range(1,len(weight)+1):
for j in range(1,capacity+1):
if j-weight[i-1] < 0:
dp[i][j] = dp[i-1][j]
lastnode[i][j] = 1 #1表示上一跳是dp[i-1][j]
else:
if dp[i-1][j-weight[i-1]]+value[i-1] > dp[i-1][j]:
dp[i][j] = dp[i-1][j-weight[i-1]]+value[i-1]
lastnode[i][j] = -1 #-1表示上一跳是dp[i-1][j-s[i]]
else:
dp[i][j] = dp[i-1][j]
lastnode[i][j] = 1 #1表示上一跳是dp[i-1][j]
print("dp:",dp)
print(dp[-1][-1])
u= len(weight)
v= capacity
track = []
for i in range(len(weight)):
if lastnode[u][v] == -1:
u = u-1
v = v-weight[len(weight)-1-i]
#print("u:",u,"v:",v)
track.append(value[len(value)-1-i])
else:
u = u-1
v = v
#print("u:",u,"v:",v)
track.reverse()
print("当前背包中装的物品为:",track)
print("当前背包的最大重量为:",sum(track))
4.实验结果
4.1实验结果
运行代码后,我们得到了下图所示的结果,与我们的推论相符,实验成功。

4.2 实验测试
用测试数据集测试五组数据的正确性:
1.
weight: [5, 6, 4, 3, 8, 4, 2]
value: [10, 1, 6, 9, 3, 4, 2]
capacity: 13
answer: 25

weight: [6, 1, 6, 1]
value: [2, 5, 6, 2]
capacity: 15
answer: 15

3.
weight: [9, 3]
value: [9, 6]
capacity: 19
answer: 15

4.
weight: [2, 1, 5, 4, 7, 4, 1, 7]
value: [4, 6, 7, 1, 1, 3, 2, 2]
capacity: 20
answer: 24

5.
weight: [8, 8, 9, 6, 10, 6]
value: [4, 2, 4, 10, 1, 1]
capacity: 16
answer: 14

5.优化策略
在状态转移方程中,计算dp[i][j]时总是只需要dp[i-1][j]左侧部分的数据。且当计算dp[i+1][]的部分时,dp[i-1]的数据就用不到了。因此,为了节省空间开销,我们可以选择使用一个一维数据存储。
6.参考和致谢
[1]胡凡,曾磊.算法笔记[M].机械工业出版社:北京,2016.7:390-392.
[2]【MIT课程】动态规划I-最短路径算法 https://www.bilibili.com/video/BV1Y441157H7
[3]漫画:什么是动态规划?(整合版) https://www.sohu.com/a/149075950_684445