AI大模型正在以惊人的速度改变着各行各业。正如移动互联网时代造就了无数成功的开发者，今天的大模型技术也为我们带来了前所未有的机遇。学习和掌握这项技术，不仅能让你站在行业前沿，还能为你的职业生涯带来巨大的回报。

01

企业为什么需要AI大模型

企业对于AI大模型的需求正以前所未有的速度增长，而这背后的原因不仅仅是为了追赶潮流，更是因为AI大模型能为企业带来切实的商业价值。

降本增效：通过AI大模型，企业可以大幅提升员工的综合能力和产值，减少人工重复劳动，从而有效降低运营成本。

产品创新：AI大模型为企业提供了重新设计和改良产品的机会，提升用户体验，使产品更具竞争力。

高性价比：行业大模型能够在相对较小的参数量下，通过低成本的再训练或精调，获得卓越的性能效果。这意味着企业可以以更少的投入，获得更高的回报。

数据安全可控：通过私有化部署，企业能够确保数据安全，减少数据泄露的风险，从而增强客户信任。

AI大模型正在成为企业提升竞争力、推动创新的重要工具，而能够掌握这项技术的人才，自然也会成为企业的核心资源。

02

学习AI大模型能给我什么

掌握AI大模型不仅对企业至关重要，对于个人的职业发展来说，更是一次不可多得的机会。

薪资溢价：大模型技术是一项稀缺技能，能够让你在薪资谈判中获得更高的薪资和职位晋升机会。

效率翻倍：AI大模型能够显著提升你的工作效率，让你在更短的时间内完成更多任务，减少加班，优化生活质量。

实现创业或兼职：通过掌握AI大模型，你可以成为一个“超级个体”，具备独立承包项目或创业的能力，从而拓宽职业发展的道路。

提升组织地位：成为公司内部的AI大模型专家，你将巩固自己的核心生态位，提升在公司中的影响力和话语权。

增强竞争力：持续学习AI大模型能够不断提升你的技能，降低降薪或裁员风险，确保在职场中稳步前行。

03

前景广阔：职业发展的新蓝海

正如当年App开发者抓住了移动互联网的浪潮一样，今天学习AI大模型也能让你站在技术变革的前沿。随着AI大模型在各行各业的广泛应用，市场对这一领域的专业人才需求只会越来越大。无论你是想进入科技巨头，还是在初创公司大展拳脚，学习AI大模型都将为你铺平职业发展的道路。

那么，我们该如何学习大模型？

作为一名热心肠的互联网老兵，我决定把宝贵的AI知识分享给大家。 至于能学习到多少就看你的学习毅力和能力了 。我已将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

一、大模型全套的学习路线

学习大型人工智能模型，如GPT-3、BERT或任何其他先进的神经网络模型，需要系统的方法和持续的努力。既然要系统的学习大模型，那么学习路线是必不可少的，下面的这份路线能帮助你快速梳理知识，形成自己的体系。

L1级别:AI大模型时代的华丽登场

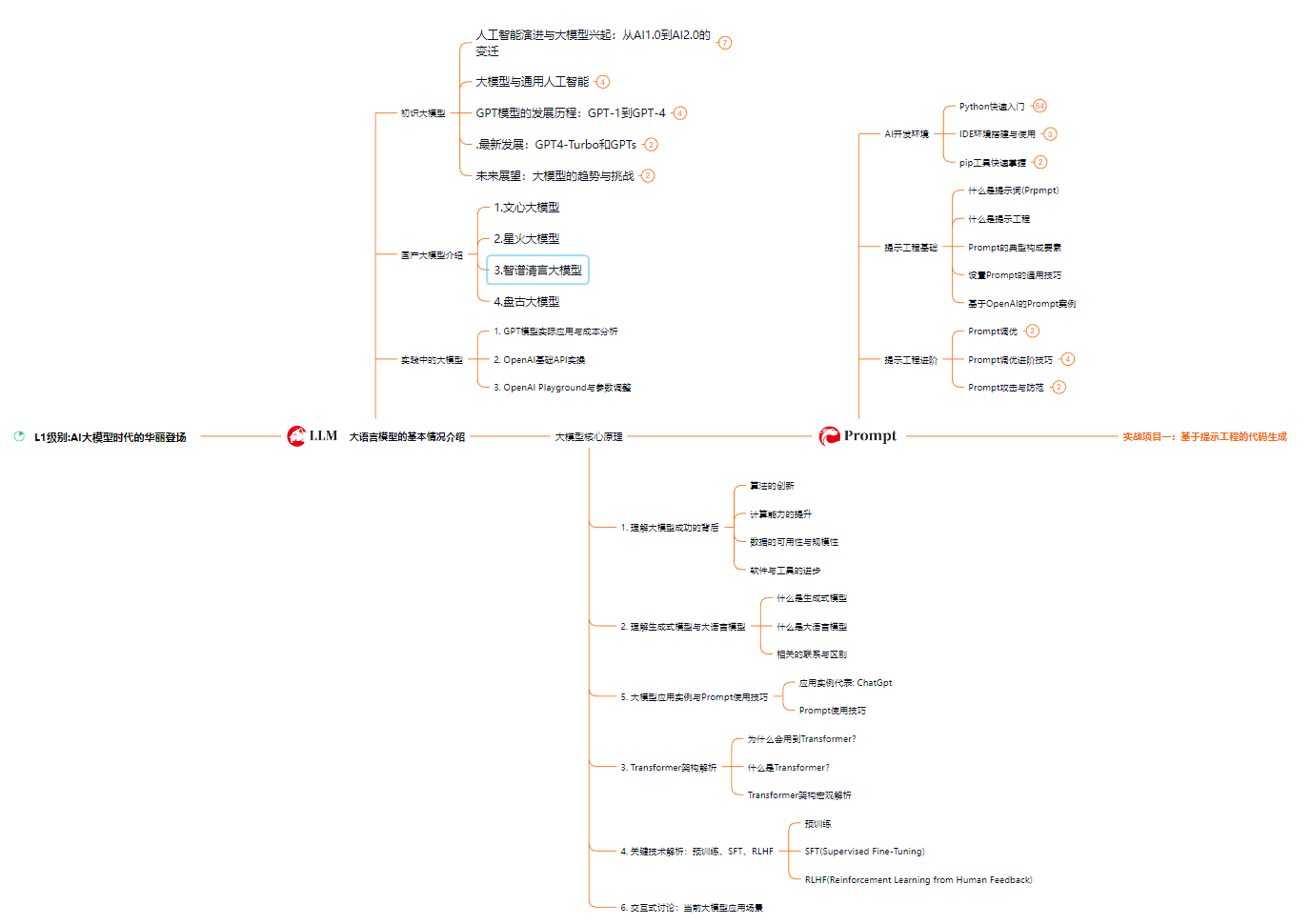
L2级别：AI大模型API应用开发工程

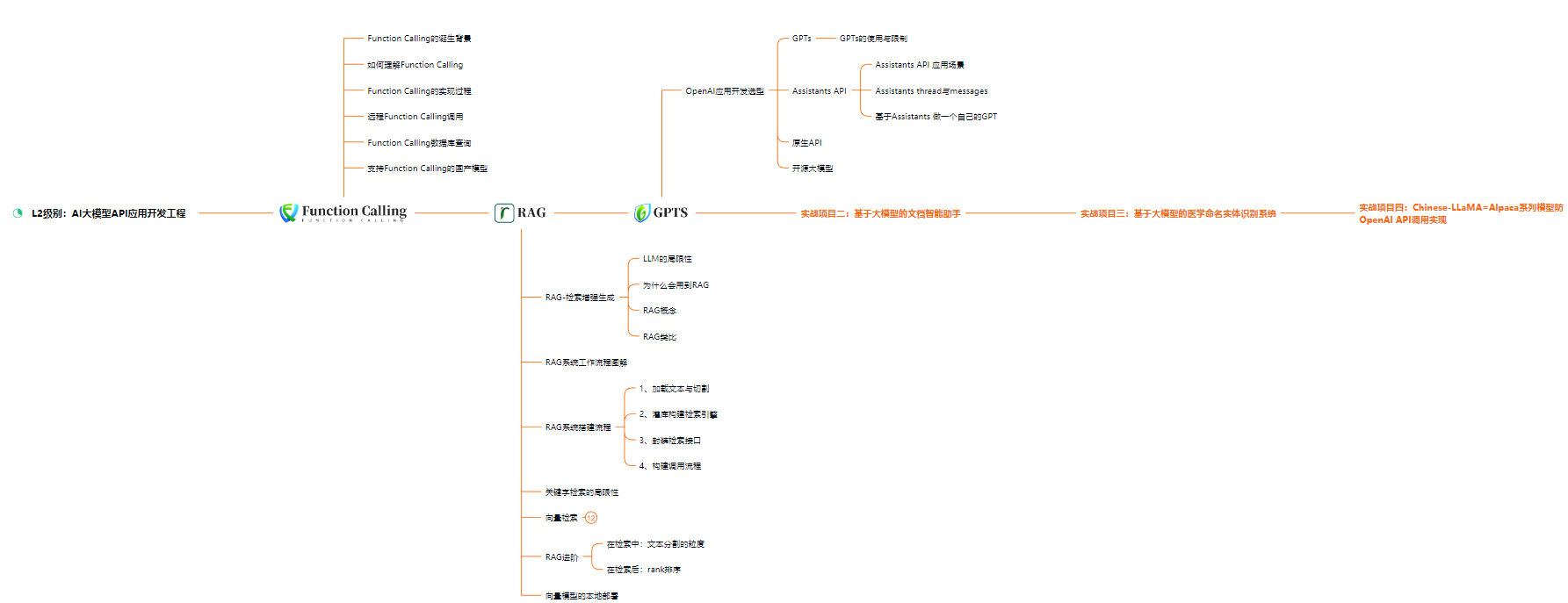
L3级别：大模型应用架构进阶实践

L4级别：大模型微调与私有化部署

一般掌握到第四个级别，市场上大多数岗位都是可以胜任，但要还不是天花板，天花板级别要求更加严格，对于算法和实战是非常苛刻的。建议普通人掌握到L4级别即可。

以上的AI大模型学习路线，不知道为什么发出来就有点糊，高清版可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】

二、640套AI大模型报告合集

这套包含640份报告的合集，涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师，还是对AI大模型感兴趣的爱好者，这套报告合集都将为您提供宝贵的信息和启示。

三、大模型经典PDF籍

随着人工智能技术的飞速发展，AI大模型已经成为了当今科技领域的一大热点。这些大型预训练模型，如GPT-3、BERT、XLNet等，以其强大的语言理解和生成能力，正在改变我们对人工智能的认识。 那以下这些PDF籍就是非常不错的学习资源。

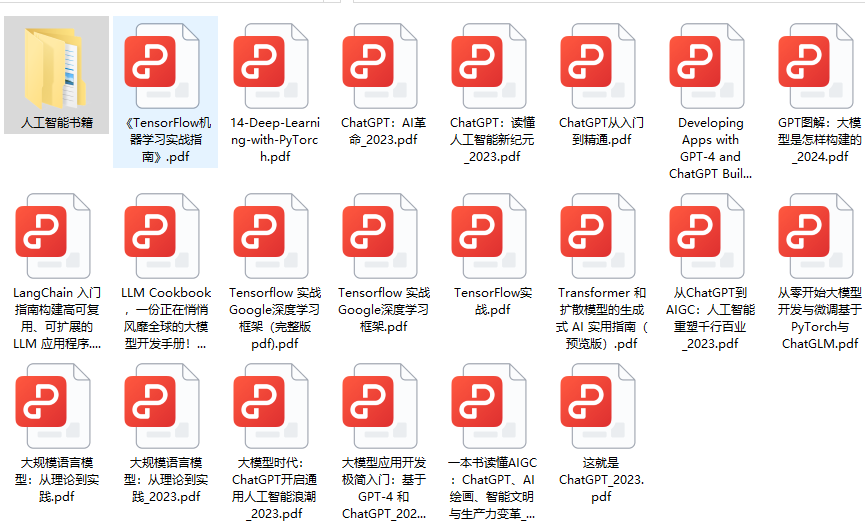
四、AI大模型商业化落地方案

作为普通人，入局大模型时代需要持续学习和实践，不断提高自己的技能和认知水平，同时也需要有责任感和伦理意识，为人工智能的健康发展贡献力量。