InCDE论文翻译
Towards Continual Knowledge Graph Embedding via Incremental Distillation
通过增量蒸馏实现持续知识图嵌入
Abstract
传统的知识图嵌入(KGE)方法通常需要在新知识出现时保留整个知识图(KG),这会带来巨大的训练成本。为了解决这个问题,提出了连续知识图嵌入(CKGE)任务,通过有效地学习新兴知识,同时保留适当的旧知识来训练 KGE 模型。然而,知识图谱中的显式图结构对于实现上述目标至关重要,但却被现有的 CKGE 方法严重忽略。一方面,现有方法通常以随机顺序学习新的三元组,破坏了新知识图谱的内部结构。另一方面,旧的三元组被同等优先地保留,未能有效缓解灾难性遗忘。在本文中,我们提出了一种基于增量蒸馏(IncDE)的CKGE竞争方法,该方法考虑了知识图谱中显式图结构的充分利用。首先,为了优化学习顺序,我们引入了分层策略,对新的三元组进行排序以进行逐层学习。通过一起使用层次间和层次内的顺序,新的三元组根据图结构特征被分组到层中。其次,为了有效地保存旧知识,我们设计了一种新颖的增量蒸馏机制,该机制有助于实体表示从上一层到下一层的无缝转移,从而促进旧知识的保存。最后,我们采用两阶段训练范式,以避免训练不足的新知识影响旧知识的过度腐败。实验结果证明 IncDE 优于最先进的基线。值得注意的是,增量蒸馏机制有助于平均倒数排名 (MRR) 分数提高 0.2%-6.5%。更多探索性实验验证了 IncDE 在熟练学习新知识同时在所有时间步骤中保留旧知识方面的有效性。
Introduction
知识图嵌入(KGE)旨在以较低的速度将知识图谱(KG)中的实体和关系嵌入到低维空间连续向量中。这对于各种知识驱动的任务至关重要,例如问答、语义搜索和关系提取。传统的 KGE 模型仅关注于获取静态知识图谱中实体和关系的嵌入。然而,现实世界的知识图谱不断发展,特别是不断出现的新知识,例如新的三元组、实体和关系。例如,在 DBpedia 从 2016 年到 2018 年的演变过程中,出现了约 100 万个新实体、2,000 个新关系和 2000 万个新三元组 (DBpedia 2021)。传统上,当知识图谱发生演化时,KGE模型需要用整个知识图谱重新训练模型,这是一个不简单的过程,训练成本巨大。在生物医学和金融等领域,更新KGE模型以通过快速发展的KG(尤其是大量新知识)支持医疗援助和明智的市场决策具有重要意义。
为此,人们提出了连续 KGE(CKGE)任务,通过仅使用新兴知识进行学习来缓解这一问题。与传统的KGE相比,CKGE的关键在于学好新兴知识,同时有效保存旧知识。如图1所示,需要学习新的实体和关系(即新的实体a、b和c)以适应新的KG。同时,旧KG中的知识(例如旧实体d)应该被保留。一般来说,现有的 CKGE 方法可以分为三个系列:基于动态架构的方法、基于重播的方法和基于正则化的方法。 基于动态架构的方法保留所有旧参数并通过新架构学习新兴知识。然而,保留所有旧参数会阻碍旧知识对新知识的适应。基于重放的方法,重放KG子图来记住旧知识,但仅回忆一部分子图会导致整个旧图结构的破坏 。基于正则化的方法旨在通过添加正则化项来保留旧知识。然而,仅向旧参数添加正则化项使得无法很好地捕获新知识。
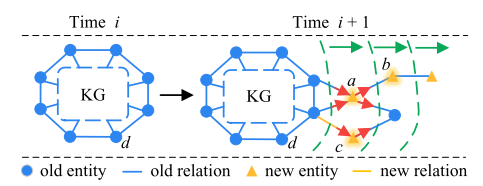
图 1:不断增长的 KG 的图示。应考虑两个特定的学习顺序:应优先考虑更接近旧KG的实体(a优先于b);应优先考虑对新三元组影响较大的实体(例如与更多关系连接)(a 优先于 c)。
尽管取得了有希望的有效性,但由于 KG 的显式图结构被严重忽视,当前的 CKGE 方法仍然表现不佳。同时,之前的研究强调了图结构在解决图相关持续学习任务中的关键作用。具体来说,现有的 CKGE 方法存在两个主要缺点:(1)首先,对于新出现的知识,当前的 CKGE 方法利用随机顺序学习策略,忽略了知识图谱中不同三元组的重要性。先前的研究表明,实体和关系的学习顺序可以显着影响图的持续学习。由于知识图谱中的知识是以图结构组织的,因此随机学习顺序可能会破坏知识图谱传达的固有语义。因此,为了有效的学习和传播,必须考虑新实体和关系的优先级。图 1 说明了一个示例,其中实体 a 应该在实体 b 之前学习,因为 b 的表示是通过旧 KG 中的 a 传播的。(2)其次,对于旧知识,当前的CKGE方法将记忆视为同等水平,导致灾难性遗忘的处理效率低下。现有研究表明,通过拓扑结构中重要节点的正则化或蒸馏来保存知识对于连续图学习至关重要。 因此,具有更本质的图结构特征的旧实体应该获得更高的保存优先级。在图 1 中,与实体 c c c 相比,连接更多其他实体的实体 a a a 应优先在时间 i + 1 i + 1 i+1 保存。
在本文中,我们提出了 IncDE,这是一种利用增量蒸馏的 CKGE 任务的新方法。IncDE旨在增强学习新兴知识的能力,同时有效地保存旧知识。首先,我们采用层次排序来确定新三元组的最佳学习序列。这涉及将三元组划分为层并通过层次间和层次内的顺序对它们进行排序。随后,有序的新兴知识被逐层学习。其次,我们引入了一种新颖的增量蒸馏机制,以有效地考虑图结构来保留旧知识。该机制结合了显式图结构,并采用逐层范式来提取实体表示。最后,我们使用两阶段训练策略来改善旧知识的保存。在第一阶段,我们修复旧实体和关系的表示。在第二阶段,我们训练所有实体和关系的表示,保护旧知识图谱免受训练不足的新兴知识的干扰。
为了评估 IncDE 的有效性,我们构建了三个具有不同规模的新知识图谱的新数据集。对现有和新的数据集进行了广泛的实验。结果表明 IncDE 优于所有强基线。此外,消融实验表明增量蒸馏可以显着提高性能。进一步的探索性实验验证了 IncDE 有效学习新兴知识同时有效保存旧知识的能力。
总结起来,本文的贡献有三方面:
- 我们提出了一种新颖的连续知识图嵌入框架 IncDE,它通过显式图结构有效地学习和保存知识。
- 我们提出分层排序以获得适当的学习顺序,以便更好地学习新兴知识。此外,我们提出了增量蒸馏和两阶段训练策略来保存良好的旧知识。
- 我们根据新知识的规模变化构建了三个新数据集。 实验表明 IncDE 的性能优于强基线。值得注意的是,增量蒸馏将 MRR 提高了 0.2%-6.5%。
Related Work
与传统的 KGE 不同,CKGE允许 KGE 模型 在记住旧知识的同时学习新知识。 现有的CKGE方法可以分为三类。(1)基于动态架构的方法:动态适应新的神经资源,以改变架构属性以响应新信息并保留旧参数。(2)基于记忆回复的方法:通过重播来保留学到的知识。 (3)基于正则化的方法:通过对更新神经权重施加约束来减轻灾难性遗忘。然而,这些方法忽视了以适当的顺序学习图数据新知识的重要性。而且,他们忽视了如何保存适当的旧知识,以便更好地融合新旧知识。CKGE 的几个数据集已经构建。然而,它们中的大多数限制新三元组至少包含一个旧实体,而忽略了没有旧实体的三元组。 在 Wikipedia 和 Yago等现实世界 KG 的演变中,出现了许多新的三元组,而没有任何旧实体。
Preliminary and Problem Statement
Growing Knowledge Graph
知识图谱 (KG) G = ( E , R , T ) \mathcal{G} = (\mathcal{E},\mathcal{R},\mathcal{T}) G=(E,R,T)包含实体 E \mathcal{E} E、关系 R \mathcal{R} R 和三元组 T \mathcal{T} T 的集合。三元组可以表示为 ( h , r , t ) ∈ T (h,r,t) \in \mathcal{T} (h,r,t)∈T,其中 h , r , t h, r,t h,r,t 分别表示头实体、关系和尾实体。当知识图谱随着时间 i i i 的新兴知识而增长时,它被表示为 G i = ( E i , R i , T i ) \mathcal{G}_{i} = (\mathcal{E}_{i},\mathcal{R}_{i},\mathcal{T}_{i}) Gi=(Ei,Ri,Ti),其中 E i , R i , T i \mathcal{E}_{i},\mathcal{R}_{i},\mathcal{T}_{i} Ei,Ri,Ti 是 G i \mathcal{G}_{i} Gi 中实体、关系和三元组的集合。此外,我们分别将 Δ T i = T i − T i − 1 \Delta\mathcal{T}_{i} = \mathcal{T}_{i}-\mathcal{T}_{i-1} ΔTi=Ti−Ti−1、 Δ E i = E i − E i − 1 \Delta\mathcal{E}_{i} = \mathcal{E}_{i}-\mathcal{E}_{i-1} ΔEi=Ei−Ei−1 和 Δ R i = R i − R i − 1 \Delta\mathcal{R}_{i} = \mathcal{R}_{i} - \mathcal{R}_{i-1} ΔRi=Ri−Ri−1 表示为新的三元组、实体和关系。
Continual Knowledge Graph Embedding
给定一个知识图谱 G \mathcal G G,知识图嵌入(KGE)旨在将实体和关系嵌入到低维向量空间 R \mathbb R R 中。给定头实体 h ∈ E h\in\mathcal{E} h∈E,关系 r ∈ R r\in\mathcal{R} r∈R 和尾实体 t ∈ E t\in\mathcal{E} t∈E,它们的嵌入表示为 h ∈ R d \mathbf{h}\in\mathbb{R}^{d} h∈Rd、 r ∈ R d \mathbf{r}\in\mathbb{R}^{d} r∈Rd 和 t ∈ R d \mathbf{t}\in\mathbb{R}^{d} t∈Rd,其中 d d d 是嵌入大小。典型的 KGE 模型包含嵌入层和评分函数。嵌入层生成实体和关系的向量表示,而评分函数在训练阶段为每个三元组分配分数。
给定时间 i i i 不断增长的知识图谱 G i \mathcal G_i Gi,连续知识图嵌入(CKGE)旨在更新旧实体 E i − 1 \mathcal{E}_{i-1} Ei−1 和关系 R i − 1 \mathcal{R}_{i-1} Ri−1 的嵌入,同时获得新实体 Δ E i \Delta\mathcal{E}_{i} ΔEi 和关系 Δ R i \Delta\mathcal{R}_{i} ΔRi 的嵌入。最后,获得所有实体 E i \mathcal{E}_{i} Ei 和关系 R i \mathcal{R}_{i} Ri 的嵌入。
Methodology
Framework Overview
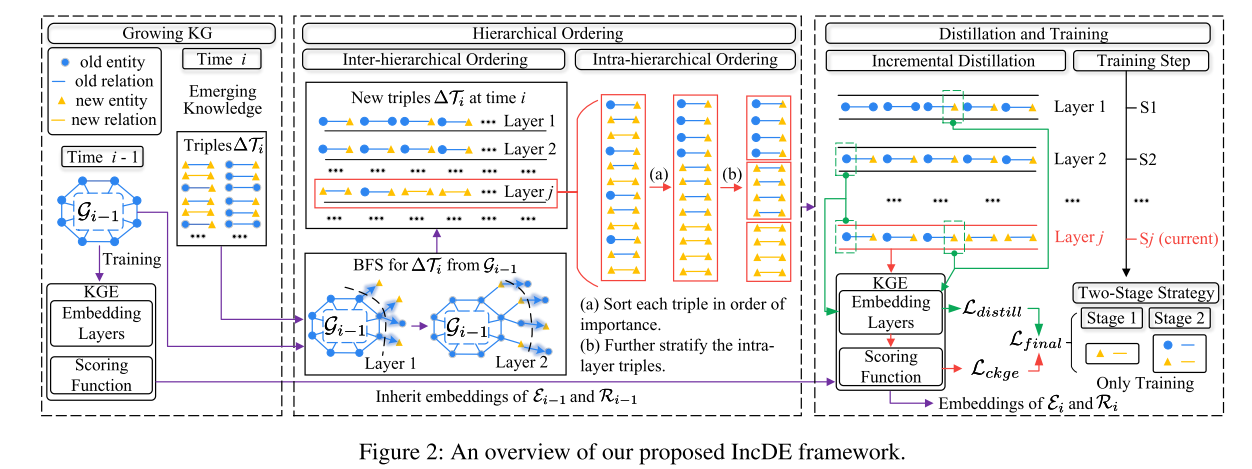
IncDE 的框架如图 2 所示。最初,当新兴知识在时间 i i i 出现时,IncDE 对新三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi 执行分层排序。具体来说,采用层次间排序,使用旧图 G i − 1 \mathcal{G}_{i-1} Gi−1 的广度优先搜索 (BFS) 扩展将 Δ T i \Delta\mathcal{T}_{i} ΔTi 划分为多个层。 随后,在每一层内应用分层内排序以进一步对三元组进行排序和划分。 然后,对分组的 Δ T i \Delta\mathcal{T}_{i} ΔTi 进行逐层训练, E i − 1 \mathcal E_{i−1} Ei−1 和 R i − 1 \mathcal R_{i−1} Ri−1 的嵌入继承自前次 i − 1 i−1 i−1 的 KGE 模型。在训练过程中,引入了增量蒸馏。准确地说,如果第 j j j 层中的实体已出现在前一层中,则其表示形式将使用与当前层最接近的层进行提取。此外,还提出了两阶段训练策略。在第一阶段,仅训练新实体 Δ E i \Delta\mathcal{E}_{i} ΔEi 和关系 Δ R i \Delta\mathcal{R}_{i} ΔRi 的表示。在第二阶段,所有实体 E i \mathcal{E}_{i} Ei和关系 R i \mathcal{R}_{i} Ri在训练过程中得到训练。最后,得到第 i i i 时刻 E i \mathcal{E}_{i} Ei 和 R i \mathcal{R}_{i} Ri 的嵌入。
Hierarchical Ordering
为了增强对新兴知识的图结构的学习,我们首先根据实体和关系的重要性,以层次间和层次内的方式对时间 i i i 的三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi 进行排序,如图 2 所示。可以预先计算以减少训练时间。然后,我们按顺序逐层学习新的三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi。具体排序策略如下。
层次间排序 对于层次间排序**,**我们在时间 i i i 将所有新三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi 拆分为多个层 l 1 , l 2 , . . . , l n l_{1},l_{2},...,l_{n} l1,l2,...,ln。由于新实体 Δ E i \Delta\mathcal{E}_{i} ΔEi 的表示是从旧实体 E i − 1 \mathcal E_{i−1} Ei−1 和旧关系 R i − 1 \mathcal R_{i−1} Ri−1 的表示传播的,因此我们根据新实体 Δ E i \Delta\mathcal{E}_{i} ΔEi 和旧图 G i − 1 \mathcal G_{i−1} Gi−1 之间的距离分割新三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi 。我们使用面包优先搜索(BFS)算法逐步将 Δ T i \Delta\mathcal{T}_{i} ΔTi 与 G i − 1 \mathcal G_{i−1} Gi−1 分开。首先,我们将旧图设为 l 0 l_0 l0。 然后,我们将所有包含旧实体的新三元组作为下一层, l 1 l_1 l1。接下来,我们将 l 1 l_1 l1 中的新实体视为看到的旧实体。重复上述两个过程,直到没有三元组可以添加到新层中。 最后,我们使用所有剩余的三元组作为最后一层。这样,我们首先将所有新的三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi 分为多层。
图结构中三元组的重要性对于实体 E i \mathcal E_{i} Ei 和关系 R i \mathcal R_{i} Ri 在时间 i i i 学习或更新的顺序也至关重要。因此对于每一层的三元组,我们根据图结构中实体和关系的重要性进一步对它们进行排序,如图2(a)所示。为了衡量实体 E i \mathcal E_{i} Ei 在新三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi 中的重要性,我们首先计算实体 e ∈ E i e\in\mathcal{E}_{i} e∈Ei 的节点中心性为 f n c ( e ) f_{nc}(e) fnc(e),如下所示:
f n c ( e ) = f n e i g h b o r ( e ) N − 1 ( 1 ) f_{nc}(e)=\frac{f_{neighbor}(e)}{N-1}\quad\quad\quad(1) fnc(e)=N−1fneighbor(e)(1)
其中 f n e i g h b o r ( e ) f_{neighbor}(e) fneighbor(e) 表示 e e e 的邻居数量, N N N 表示在时间 i i i 时新三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi 中的实体数量。然后,为了衡量关系 R i \mathcal R_{i} Ri 在每层三元组中的重要性,我们将关系 r ∈ R i r\in\mathcal R_{i} r∈Ri 的介数中心性计算为 f b c ( r ) f_{bc}(r) fbc(r):
f b c ( r ) = ∑ s , t ∈ E i , s ≠ t σ ( s , t ∣ r ) σ ( s , t ) ( 2 ) f_{bc}(r)=\sum_{s,t\in\mathcal{E}_{i},s\neq t}\frac{\sigma(s,t|r)}{\sigma(s,t)}\quad\quad\quad(2) fbc(r)=s,t∈Ei,s=t∑σ(s,t)σ(s,t∣r)(2)
其中 σ ( s , t ) \sigma(s, t) σ(s,t) 是新三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi 中 s s s 和 t t t 之间的最短路径的数量, σ ( s , t ∣ r ) \sigma(s,t|r) σ(s,t∣r) 是经过关系 r r r 的 σ ( s , t ) \sigma(s, t) σ(s,t) 的数量。具体来说,我们只计算新兴KG的 f n c f_{nc} fnc 和 f b c f_{bc} fbc,避免图表过多。为了获得三元组 ( h , r , t ) (h,r,t) (h,r,t)在每一层中的重要性,我们计算该三元组中头实体 h h h 的节点中心性、尾实体 t t t 的节点中心性以及关系 r r r 的介数中心性。考虑到图结构中实体和关系的整体重要性,我们一起采用 f n c f_{nc} fnc 和 f b c f_{bc} fbc。 每个三元组的最终重要性可以计算为:
I T ( h , r , t ) = m a x ( f n c ( h ) , f n c ( t ) ) + f b c ( r ) ( 3 ) IT_{(h,r,t)}=max(f_{nc}(h),f_{nc}(t))+f_{bc}(r)\quad(3) IT(h,r,t)=max(fnc(h),fnc(t))+fbc(r)(3)
我们根据 I T IT IT 值对每一层的三元组进行排序。分层内排序的利用保证了对每层图结构重要的三元组的优先级。反过来,这可以更有效地学习新图的结构。
此外,层次内排序可以帮助进一步拆分层内三元组,如图 2 (b) 所示。由于每层中的三元组数量由新图的大小决定,因此它可能太大而无法学习。为了防止特定层中的三元组数量过多,我们将每层中的三元组的最大数量设置为 M M M。如果一层中的三元组数量超过 M M M,则可以分割成不超过 M M M个三元组的若干层 在层次结构内部的排序中。
Distillation and Training
分层排序后,我们在时间 i i i 逐层训练新的三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi。我们采用 TransE 作为基本 KGE 模型。当训练第 j j j 层 ( j > 0 ) (j > 0) (j>0)时,原始 TransE 模型的损失为:
L c k g e = ∑ ( h , r , t ) ∈ l j m a x ( 0 , f ( h , r , t ) − f ( h ′ , r , t ′ ) + γ ) ( 4 ) \mathcal{L}_{ckge}=\sum_{(h,r,t)\in l_j}max(0,f(h,r,t)-f(h',r,t')+\gamma) \quad(4) Lckge=(h,r,t)∈lj∑max(0,f(h,r,t)−f(h′,r,t′)+γ)(4)
其中 ( h ′ , r , t ′ ) (h',r,t') (h′,r,t′) 是 ( h , r , t ) ∈ l j (h,r,t) \in l_j (h,r,t)∈lj 的负三元组,而 f ( h , r , t ) = ∣ h + r − t ∣ L 1 / L 2 f(h,r,t)=|h+r-t|_{L1/L2} f(h,r,t)=∣h+r−t∣L1/L2 是 TransE的得分函数。我们在时间 i − 1 i−1 i−1 时从 KGE 模型继承旧实体 E i − 1 \mathcal{E}_{i-1} Ei−1 和关系 R i − 1 \mathcal{R}_{i-1} Ri−1 的嵌入,并随机初始化新实体 Δ E i \Delta\mathcal{E}_{i} ΔEi 和关系 Δ R i \Delta\mathcal{R}_{i} ΔRi 的嵌入。
在训练过程中,我们使用增量蒸馏来保留旧知识。此外,我们提出了一种两阶段训练策略,以防止旧实体和关系的嵌入在训练开始时被过度破坏。
增量蒸馏 为了减轻在先前层中学习的实体的灾难性遗忘,受到 KGE 模型知识蒸馏的启发,我们蒸馏了以下实体表示: 当前层与先前层中出现的实体如图 2 所示。具体来说,如果第 j (j > 0) 层中的实体 e e e 已出现在先前层中,我们将其与 e e e 的表示形式进行提取 最近的层。 实体 e k ( k ∈ [ 1 , ∣ E i ∣ ] ) e_k(k\in[1,|\mathcal{E}_i|]) ek(k∈[1,∣Ei∣]) 的蒸馏损失为:
L d i s t i l l k = { 1 2 ( e ′ k − e k ) 2 , ∣ e ′ k − e k ∣ ≤ 1 ∣ e ′ k − e k ∣ − 1 2 , ∣ e ′ k − e k ∣ > 1 ( 5 ) \left.\mathcal{L}_{distill}^k=\left\{\begin{array}{ll}\frac{1}{2}(\mathbf{e'}_k-\mathbf{e}_k)^2,&|\mathbf{e'}_k-\mathbf{e}_k|\leq1\\|\mathbf{e'}_k-\mathbf{e}_k|-\frac{1}{2},&|\mathbf{e'}_k-\mathbf{e}_k|>1\end{array}\right.\right.\quad\quad(5) Ldistillk={21(e′k−ek)2,∣e′k−ek∣−21,∣e′k−ek∣≤1∣e′k−ek∣>1(5)
其中 e k e_k ek 表示第 j j j 层中实体 e k e_k ek 的表示, e k ′ e^\prime_k ek′ 表示最近一层的实体 e k e_k ek 的表示。通过提炼先前层中出现的实体,我们可以有效地记住旧知识。然而,不同的实体对于过去的表征应该有不同程度的记忆。图结构中重要性较高的实体应在蒸馏过程中优先考虑并更大程度地保留。除了实体 f n c f_{nc} fnc 的节点中心性之外,与关系的介数中心性类似,我们将实体 e e e 在时间 i i i 的介数中心性 f b c ( e ) f_{bc}(e) fbc(e) 定义为:
f b c ( e ) = ∑ s , t ∈ E i , s ≠ t σ ( s , t ∣ e ) σ ( s , t ) ( 6 ) f_{bc}(e)=\sum_{s,t\in\mathcal{E}_i,s\neq t}\frac{\sigma(s,t|e)}{\sigma(s,t)}\quad\quad(6) fbc(e)=s,t∈Ei,s=t∑σ(s,t)σ(s,t∣e)(6)
我们结合 f b c ( e ) f_{bc}(e) fbc(e) 和 f n c ( e ) f_{nc}(e) fnc(e) 来评估实体 e e e 的重要性。具体来说,在训练第 j j j 层时,对于在时间 i i i 出现的每个新实体 e k e_k ek,我们计算 f b c ( e k ) f_{bc}(e_k) fbc(ek)和 f n c ( e k ) f_{nc}(e_k) fnc(ek)以获得初步权重 λ k \lambda_k λk为:
λ k = λ 0 ⋅ ( f b c ( e k ) + f n c ( e k ) ) ( 7 ) \lambda_k=\lambda_0\cdot(f_{bc}(e_k)+f_{nc}(e_k))\quad\quad(7) λk=λ0⋅(fbc(ek)+fnc(ek))(7)
其中,对于先前层中已出现的新实体 λ 0 \lambda_0 λ0 为 1;对于尚未出现的新实体 λ 0 \lambda_0 λ0 为 0。同时,我们学习一个矩阵 W ∈ R 1 × ∣ E i ∣ \mathbf{W}\in\mathbb{R}^{1\times|\mathcal{E}_{i}|} W∈R1×∣Ei∣ 动态改变不同实体的蒸馏损失权重。 动态蒸馏重量为:
[ λ 1 ′ , λ 2 ′ , . . . , λ ∣ E i ∣ ′ ] = [ λ 1 , λ 2 , . . . , λ ∣ E i ∣ ] ∘ W ( 8 ) [\lambda_1^{\prime},\lambda_2^{\prime},...,\lambda_{|\mathcal{E}_i|}^{\prime}]=[\lambda_1,\lambda_2,...,\lambda_{|\mathcal{E}_i|}]\circ\mathbf{W}\quad\quad(8) [λ1′,λ2′,...,λ∣Ei∣′]=[λ1,λ2,...,λ∣Ei∣]∘W(8)
其中 ∘ \circ ∘ 表示 Hadamard 产品。每层 j j j 在时间 i i i 的最终蒸馏损失为:
L d i s t i l l = ∑ k = 1 ∣ E i ∣ λ k ′ ⋅ L d i s t i l l k ( 9 ) \mathcal{L}_{distill}=\sum_{k=1}^{|\mathcal{E}_i|}\lambda_k^{^{\prime}}\cdot\mathcal{L}_{distill}^k\quad\quad(9) Ldistill=k=1∑∣Ei∣λk′⋅Ldistillk(9)
当训练第 j j j层时,最终的损失函数可以计算为:
L f i n a l = L c k g e + L d i s t i l l ( 10 ) \mathcal{L}_{final}=\mathcal{L}_{ckge}+\mathcal{L}_{distill}\quad\quad(10) Lfinal=Lckge+Ldistill(10)
经过对新三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi的逐层训练,得到实体 E i \mathcal{E}_{i} Ei和关系 R i \mathcal{R}_{i} Ri的所有表示。
两阶段训练 在训练过程中,当在时间 i i i 将新三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi 合并到现有图 G i − 1 \mathcal G_{i−1} Gi−1 中时,新三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi 中不存在的旧实体和关系的嵌入保持不变。然而,新三元组 Δ T i \Delta\mathcal{T}_{i} ΔTi 中包含的旧实体和关系的嵌入会被更新。因此,在每个时间i的初始阶段,旧图 G i − 1 \mathcal G_{i−1} Gi−1中实体 E i − 1 \mathcal E_{i−1} Ei−1和关系 R i − 1 \mathcal R_{i−1} Ri−1的部分表示将被未完全训练的新实体 Δ E i \Delta\mathcal{E}_{i} ΔEi和关系 Δ R i \Delta\mathcal{R}_{i} ΔRi破坏。为了解决这个问题,IncDE 使用两阶段训练策略来更好地保留旧图中的知识,如图 2 所示。在第一个训练阶段,IncDE 冻结所有旧实体 E i − 1 \mathcal E_{i−1} Ei−1 和关系 R i − 1 \mathcal R_{i−1} Ri−1 的嵌入并仅训练新实体 Δ E i \Delta\mathcal{E}_{i} ΔEi 和关系 Δ R i \Delta\mathcal{R}_{i} ΔRi 的嵌入。 然后,IncDE 在第二个训练阶段训练新图中所有实体 E i \mathcal E_{i} Ei 和关系 R i \mathcal R_{i} Ri 的嵌入。通过两阶段训练策略,IncDE 可以防止旧图的结构在早期训练阶段被新三元组破坏。 同时,旧图中和新图中实体和关系的表示可以在训练过程中更好地相互适应。
Experiments
Experimental Setup
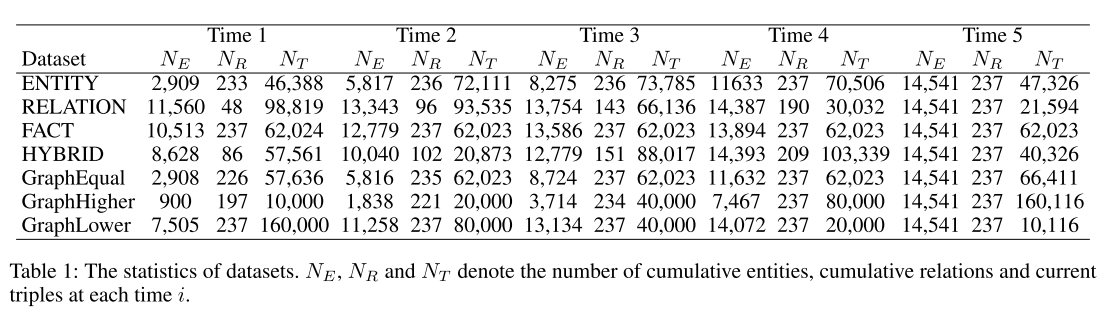
数据集 我们使用 CKGE 的七个数据集,包括四个公共数据集:ENTITY、RELATION、FACT、HYBRID,以及我们构建的三个新数据集:GraphEqual、GraphHigher 和 GraphLower。在 ENTITY、RELATION 和 FACT 中,实体、关系和三元组的数量在每个时间步均匀增加。在 HYBRID 中,实体、关系和三元组的总和随着时间的推移均匀增加。然而,这些数据集限制了知识的增长,要求新的三元组至少包含一个现有实体。为了解决这个限制,我们放宽了这些约束并构建了三个新的数据集:GraphEqual、GraphHigher 和 GraphLower。在 GraphEqual 中,三元组的数量在每个时间步始终以相同的增量增加。在 GraphHigher 和 GraphLower 中,三元组的增量分别变得更高和更低。所有数据集的详细统计数据如表 1 所示。时间步长设置为 5。每个时间步长的训练集、有效集和测试集按 3:1:1 的比例分配。 数据集可在 https://github.com/seukgcode/IncDE 获取。
基线 我们选择两种基线模型:非持续学习方法和基于持续学习的方法。首先,我们选择一种非连续学习方法 Fine-tune,每次都会使用新的三元组进行微调。然后,我们选择三种基于持续学习的方法:基于动态架构、基于记忆重放的基线和基于正则化。具体来说,基于动态架构的方法是 PNN 和 CWR。基于记忆重放的方法有 GEM 、EMR 和 DiCGRL。基于正则化的方法有 SI、EWC和 LKGE。
指标 我们评估我们的模型在链接预测任务上的性能。特别是,我们用所有其他实体替换测试集中三元组的头或尾实体,然后计算每个三元组的分数并对其进行排名。然后,我们计算 MRR、Hits@1 和 Hits@10 作为指标。MRR、Hits@1、Hits@3 和 Hits@10 越高,模型效果越好。在时间 i i i,我们使用时间 [ 1 , i ] [1, i] [1,i] 在所有测试集上测试的指标的平均值作为最终指标。主要结果是从上次生成的模型中得到的。
设置 所有实验均在 NVIDIA RTX 3090Ti GPU 上使用 PyTorch 实施。在所有实验中,我们将 TransE 设置为基本 KGE 模型,时间 i i i 的最大大小为 5。实体和关系的嵌入大小为 200。我们在 [ 512 , 1024 , 2048 ] [512, 1024, 2048] [512,1024,2048] 中调整批处理大小。我们选择 Adam 作为优化器,并从 [ 1 e − 5 , 1 e − 4 , 1 e 3 ] [1e^{-5}, 1e^{-4}, 1e^3] [1e−5,1e−4,1e3] 中设置学习率。在我们的实验中,我们在 [ 512 , 1024 , 2048 ] [512,1024,2048] [512,1024,2048]中设置每层 M M M中三元组的最大数量。为了保证公平性,所有实验结果均为5次运行的平均值。
Results
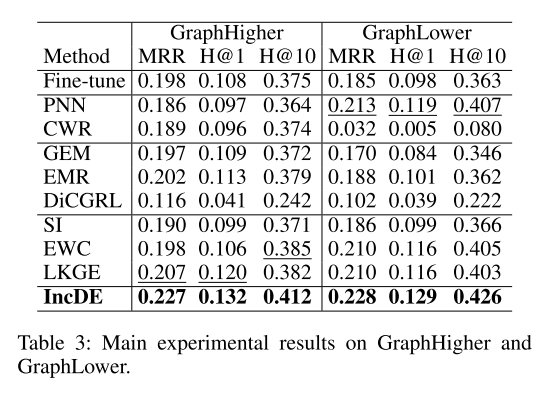
主要结果 表 2 和表 3 报告了七个数据集的主要实验结果。
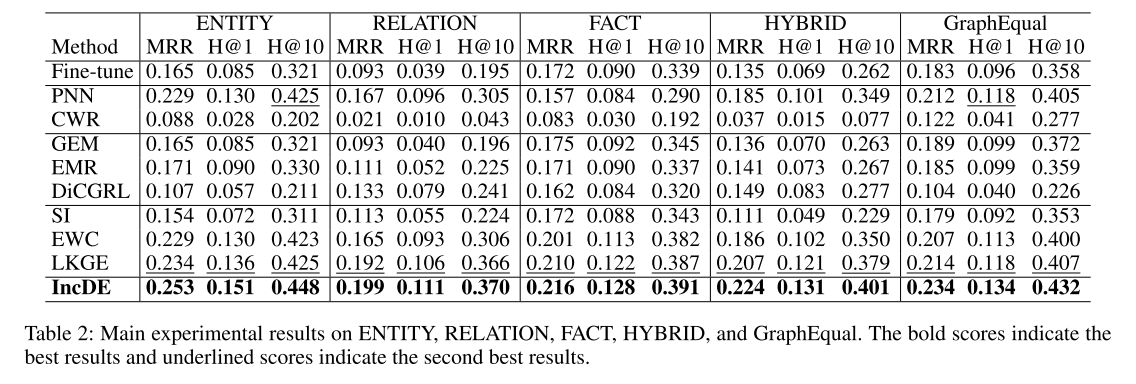
首先,值得注意的是,与 Fine-tune 相比,IncDE 表现出了相当大的改进。具体来说,与 Fine-tune 相比,IncDE 的 MRR 提高了 2.9% - 10.6%,Hits@1 提高了 2.4% - 7.2%,Hits@10 提高了 3.7% - 17.5%。结果表明,直接微调会导致灾难性遗忘。
其次,IncDE 优于所有 CKGE 基线。值得注意的是,与基于动态架构的方法(PNN 和 CWR)相比,IncDE 在 MRR、Hits@1 和 Hits@10 方面分别实现了1.5% - 19.6%、1.0% - 12.4% 和 1.9% - 34.6% 的改进。与基于重放的基线(GEM、EMR 和 DiCGRL)相比,IncDE 在 MRR、Hits@1 和 Hits@10 方面分别提高了2.5% - 14.6%、1.9% - 9.4% 和 3.3% - 23.7%。此外,与基于正则化的方法(SI、EWC 和 LKGE)相比,IncDE 在 MRR、Hits@1 和 Hits@10 方面获得了 0.6% - 11.3%、0.5% - 8.2% 和 0.4%-17.2% 的改进。这些结果证明了 IncDE 在增长 KG 方面的卓越性能。
第三,与强基线相比,IncDE 在不同类型的数据集上表现出明显的改进。在知识增长相同的数据集中(ENTITY、FACT、RELATION、HYBRID 和 GraphEqual),IncDE 的 MRR 比最先进的方法平均提高了 1.4%。在知识增长不均的数据集中(GraphHigher 和 GraphLower),IncDE 的 MRR 比最优方法提高了1.8% - 2.0%。这意味着IncDE特别适合涉及知识增长不平等的场景。值得注意的是,在处理更真实的场景感知数据集 GraphHigher 时,其中出现了大量新知识,与其他最强基线相比,IncDE 在 MRR 方面表现出最明显的优势,提高了2.0%。这表明当大量新知识出现时,IncDE 表现良好。因此,我们在不同大小的数据集(GraphHigher、GraphLower 和 GraphEqual)(从 10K 到 160K、从 160K 到 10K 以及剩余的 62K)中验证 IncDE 的可扩展性。特别是,我们观察到,与所有基线中的最佳结果相比,IncDE 在 RELATION 和 FACT 上的 MRR 仅提高了 0.6% - 0.7%,其中的改进与其他数据集相比并不显着。这可以归因于这两个数据集中新实体的增长有限,这表明 IncDE 对于实体数量变化较大的情况具有很强的适应性。现实生活中,实体之间的关系数量保持相对稳定,而大量出现的却是实体本身。这就是 IncDE 适应性强的地方。凭借其强大的能力,IncDE可以有效处理众多实体及其对应关系,确保无缝集成和高效处理。
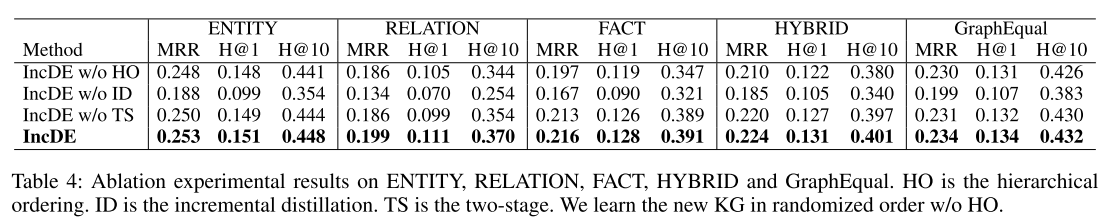
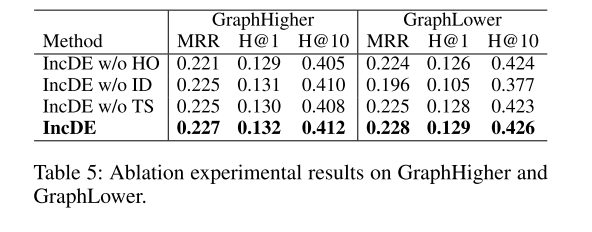
消融实验 我们研究了分层排序、增量蒸馏和两阶段训练策略的影响,如表 4 和表 5 所示。首先,当我们删除增量蒸馏时,模型性能显着下降。具体来说,MRR 指标下降了 0.2% - 6.5%,Hits@1 指标下降了 0.1% - 5.2%,Hits@10 指标下降了0.2% - 11.6%。这些发现强调了增量蒸馏在有效保留旧图的结构同时学习新图的表示方面的关键作用。其次,当我们消除分层排序和两阶段训练策略时,模型性能略有下降。具体来说,MRR指标下降了0.2% - 1.8%,Hits@1下降了0.1% - 1.8%,Hits@10下降了0.2% - 4.4%。结果表明,分层排序和两阶段训练提高了 IncDE 的性能。
IncDE 每次的表现 图3显示了 IncDE 在不同时间记住旧知识的程度。首先,我们观察到在几个测试数据上(ENTITY 中的 D1、D2、D3、D4;HYBRID 中的 D3、D4),IncDE 的性能随着时间的增加略有下降 0.2% - 3.1%。 特别是,IncDE 的性能在多个数据集上没有出现明显下降,例如 HYBRID 的 D1(时间 2 到时间 4)和 GraphLower 的 D2(时间 2 到时间 5)。这意味着 IncDE 可以很好地记住大多数数据集上的旧知识。 其次,在一些数据集上,随着继续训练,IncDE 的性能意外提高。 具体来说,IncDE的性能在MRR中GraphLower的D3上逐渐提高了0.6%。 这表明 IncDE 很好地学习了新兴知识,并用新兴知识增强了旧知识。
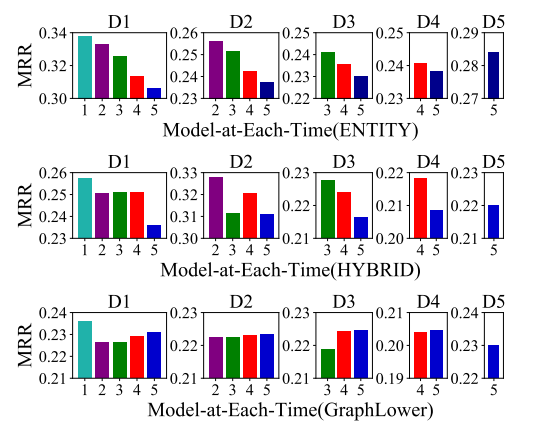
图 3:IncDE 每次在 ENTITY、HYBRID 和 GraphLower 上的有效性。不同的颜色代表不同时间生成的模型的性能。 D i Di Di 表示时间 i i i 的测试集。
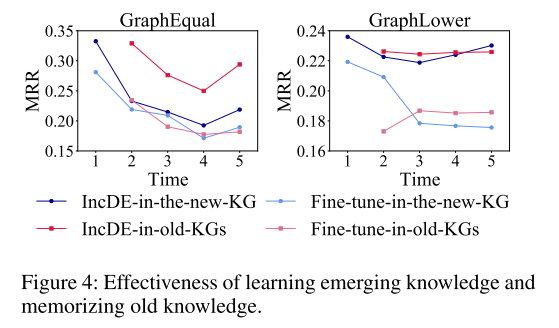
学习和记忆的效果 为了验证IncDE能够很好地学习新兴知识并有效地记住旧知识,我们分别研究了IncDE和Fine-tune每次对新KG和旧KG的影响,如图4所示 为了评估旧 KG 的性能,我们计算了所有过去时间步长的 MRR 平均值。首先,我们观察到 IncDE 在新 KG 上的表现优于 Fine-tune,MRR 更高,范围为 0.5% 到 5.5%。这表明 IncDE 能够有效地学习新兴知识。其次,IncDE 在 MRR 上比旧 KG 上的 Fine-tune 高出 3.8%-11.2%。这些发现表明,IncDE 减轻了灾难性遗忘的问题,并实现了更有效地保留旧知识。
最大层尺寸的影响 为了研究增量蒸馏中每层最大尺寸M对模型性能的影响,我们研究了最后一次具有不同M的IncDE模型的性能,如图5所示。首先,我们发现随着 M M M 在 [128, 1024] 范围内,所有数据集上的模型性能都会提高。这表明,一般来说, M M M 越高,增量蒸馏的影响就越大。其次,当 M M M 达到 2048 时,我们观察到一些数据集的性能显着下降。这意味着太大的 M 可能导致层数太少并限制增量蒸馏的性能。根据经验, M = 1024 M=1024 M=1024 是大多数数据集中的最佳大小。这进一步证明有必要限制每层学习的三元组数量。
案例研究 为了进一步探讨 IncDE 保存旧知识的能力,我们进行了全面的案例研究,如表 6 所示。在预测亚利桑那州立大学的主要研究领域的情况下,IncDE 将正确答案计算机科学排在 排名第一,优于排名第二或第三的其他强基线,例如 EWC、PNN 和 LKGE。 这表明虽然其他方法在一定程度上忘记了过去时间的知识,但 IncDE 可以准确地记住每个时间的旧知识。 此外,当删除增量蒸馏(ID)时,IncDE 无法预测前三个位置中的正确答案。 这表明,在不进行增量蒸馏的情况下预测旧知识时,IncDE 的性能显着下降。 相反,在去除层次排序(HO)和两阶段训练策略(TS)后,IncDE仍然准确地预测出第一个位置的正确答案。 这一观察有力地支持了这样一个事实:增量蒸馏为 IncDE 在保存旧知识方面提供了相对于其他强基线的关键优势。
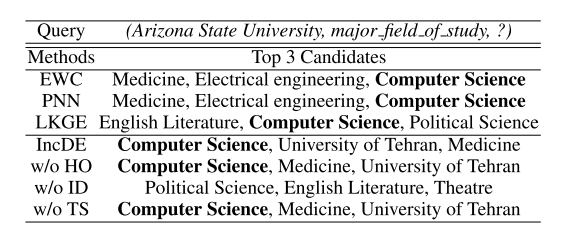
表 6:案例研究的结果。我们使用时间 5 生成的模型,并随机选择时间 1 出现在 ENTITY 中的查询进行预测。 斜体是查询结果,粗体是真实的预测结果。
Discussion
IncDE的新颖性 IncDE的新颖性可以概括为以下两个方面。(1)高效的知识保存蒸馏。虽然 IncDE 采用蒸馏方法,但它与之前的 KGE 蒸馏方法不同。一方面,与其他主要提取最终分布的 KGE 蒸馏方法相比,增量蒸馏(ID)提取了中间隐藏状态。这种方式巧妙地保留了旧知识的基本特征,使其能够适应各种下游任务。另一方面,只有 ID 才能从模型本身传输知识,因此与从其他模型传输知识相比可以减少错误传播。(2)显式的图感知机制。 与其他 CKGE 基线相比,IncDE 通过将图结构融入持续学习而脱颖而出。 这种显式的图感知机制使 IncDE 能够利用图内编码的固有语义,使其能够智能地确定最佳学习顺序并有效平衡旧知识的保存。
IncDE 中的三个组件 IncDE 的三个组件:分层排序 (HO)、增量蒸馏 (ID) 和两阶段训练 (TS) 本质上相互依赖,并且需要一起使用。我们从以下两个方面来解释。 (一)设计原则。IncDE 的根本动机在于有效学习新兴知识,同时保留旧知识。此目标由所有三个组件实现:HO、ID 和 TS。一方面,HO起到将新三元组分层的作用,优化新知识的学习过程。另一方面,ID和TS试图提取和保存实体的表示,确保旧知识的有效保存。(2)相互依存。 这三个组成部分本质上是相互关联的,应该一起使用。一方面,HO 在生成新三元组的分区方面发挥着至关重要的作用,这些新三元组随后被输入到 ID 中。另一方面,通过使用 TS,ID 可以防止旧实体在早期训练阶段被破坏。
增量蒸馏的意义 尽管 IncDE 提出的三个组件:增量蒸馏(ID)、分层排序(HO)和两阶段训练(TS)对于 CKGE 任务都有效,但 ID 是其中的中心模块。理论上,持续学习任务的主要挑战是逐步学习时发生的灾难性遗忘,这也适合CKGE任务。为了应对这一挑战,ID 引入了显式图结构来提取实体表示,在整个训练期间有效地逐层保留旧知识。然而,HO专注于很好地学习新知识,而TS只能缓解训练初期的灾难性遗忘。因此,ID在CKGE任务的所有组件中起着最重要的作用。在实验中,我们从表4和表5观察到,与HO(MRR平均0.9%)和TS(MRR平均0.5%)相比,ID表现出显着的改善(MRR平均4.1%)。这样的结果进一步验证 与 HO 和 TS 相比,ID 是关键组件。 这三个组件相互作用,共同完成CKGE任务。
Conclusion
本文提出了一种新颖的连续知识图嵌入方法 IncDE,该方法结合知识图谱的图结构来学习新知识和记住旧知识。首先,我们对新知识图谱中的三元组进行层次排序,以获得最优的学习序列。其次,我们提出增量蒸馏,以在逐层训练新三元组时保留旧知识。此外,我们通过两阶段训练策略优化训练过程。 未来我们会考虑如何处理随着知识图的演化旧知识被删除的情况。 此外,必须解决跨领域和异构数据集成到扩展知识图谱中的问题。
论文链接:
https://arxiv.org/pdf/2405.04453
GitHub:
https://github.com/seukgcode/IncDE

![[C++][opencv]基于opencv实现photoshop算法可选颜色调整](https://i-blog.csdnimg.cn/direct/e99672cffc4f4999b41ebd88fe91636b.gif)