3.最短路径

在网图和非网图中，最短路径的含义是不同的。

由于非网图它没有边上的权值，所谓的最短路径，其实就是指两顶点之间经过的边数最少的路径。

对于网图来说，最短路径，是指两顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第一个顶点是源点，最后一个顶点是终点。

• 单源最短路径
  • BFS(广度优先算法)算法（无权图）
  • 迪杰斯特拉(Dijkstra)算法（无权图、带权图）
• 各个顶点之间的最短路径
  • 弗洛伊德(Floyd)算法（无权图、带权图）

3.1 BFS 算法

【技巧】不带权值图其实就是一直特殊的带权图，只是权值都是1。

通过一次遍历，就得到了每个结点到源点的距离。所以求最短路径的代码可以通过BFS遍历得到：

//BFS广度遍历算法求最短路径
void BFS_MIN_Distance(MGraph G, int v){
    Queue Q;
	InitQueue(&Q);	//初始化一辅助用的队列
    
    //d[i]表示从u到i结点的最短路径
    for(int i=0; i<G.numVertexes; ++i){
    	d[i] = 32767;	//初始化为无穷，意为不相连
    	path[i]=-1;		//最短路径从哪个顶点过来，就上这条路的上一个结点，这里是源点所以是-1
    }
    
//源点处理
    d[v]=0;		//结点本身，距离为0
    visit(v);	//访问顶点
    vivited[v]=TRUE;	//设置当前访问过
    EnQueue(&Q, v);	//将此顶点入队列

//BFS
    while(!QueueEmpty(Q)){
        DeQueue(&Q, &v);	//顶点i出队列
        for(w=FirstNeighbor(G, v); w>=0; w=NextNeighbor(G, v, w)){
            //检验v的所有邻接点
            if(!visited[w]){
                d[w]=d[v]+1	//路径长度+1
                path[w]=v;	//w的上一个结点是v
                visit(w);	//访问顶点w
                visited[w]=TRUE;	//访问标记
                EnQueue(Q, w);	//顶点w入队列
            }//if
        }//for
    }//while
}

3.2 迪杰斯特拉(Dijkstra)算法

Dijkstra算法[1]用于构建单源点的最短路径—，即图中某个点到任何其他点的距离都是最短的。例如，构建地图应用时查找自己的坐标离某个地标的最短距离。可以用于有向图，但是不能存在负权值。

6.4_3_最短路径问题_Dijkstra算法_哔哩哔哩_bilibili

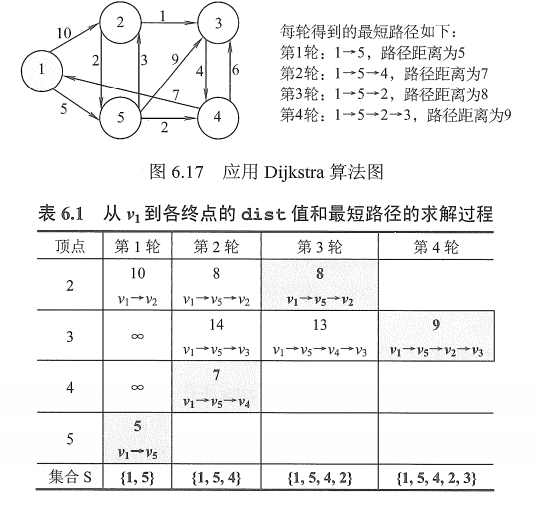
【注意】Dijkstra算法不适用于有负权值的带权图。

显然，Dijkstra算法也是基于贪心策略的。使用邻接矩阵或者带权的邻接表表示时，时间复杂度为O(|V|²)。

3.3 弗洛伊德(Floyd)算法

弗洛伊德(Floyd)算法是用来求任意两个结点之间的最短路的。

复杂度比较高，但是常数小，容易实现（只有三个 for）。

【适用】适用于任何图，不管有向无向，边权正负，但是最短路必须存在。（不能有个负环）

6.4_4_最短路径问题_Floyd算法_哔哩哔哩_bilibili

使用动态规划思想，将问题的求解分为多个阶段

对于n个顶点的图G，求任意一对顶点Vi -> Vj之间的最短路径可分为如下几个阶段：

• 初始︰不允许在其他顶点中转，最短路径是?
• 0：若允许在Vo中转，最短路径是?
• 1：若允许在Vo、V中转，最短路径是?
• 2：若允许在Vo、V1、Vz中转，最短路径是?
• …
• n-1∶若允许在Vo、V1、V2…Vn-1中转，最短路径是?

例子：

1. 初始化：方阵$A^{(-1)}[i][j]=arcs[i][j]$.

2. 第一轮：将$V_0$作为中间顶点，对于所有顶点 { i , j } \{i,j\} {i,j}，如果有$A^{-1}[i][j]>A^{-1}[i][0]+A^{-1}[0][j]$，则将$A^{-1}[i][j]$更新为$A^{-1}[i][0]+A^{-1}[0][j]$.

   eg:有$A^{-1}[2][1]>A^{-1}[2][0]+A^{-1}[0][1]=11$，更新$A^{-1}[2][1]=11$，更新后的方阵标记为$A^0$。

3. 第二轮：将$V_1$作为中间顶点，继续监测全部顶点对 { i , j } \{i,j\} {i,j}.

   eg:有$A^0[0][2]>A^0[0][1]+A^0[1][2]=10$，更新后的方阵标记为$A^1$。

4. 第三轮：将$V_2$作为中间顶点，继续监测全部顶点对 { i , j } \{i,j\} {i,j}.

   eg:有$A^1[1][0]>A^1[1][2]+A^1[2][0]=9$，更新后的方阵标记为$A^2$。

此时$A^2$中保存的就是任意顶点对的最短路径长度。

应用Floyd算法求所有顶点之间的最短路径长度的过程如下表所示：

从这个表中，可以发下一些规律：

可以看出，矩阵中，每一步中红线划掉的部分都不用考虑计算，只需要计算红线外的部分，节省了计算量。

---

但是代码很简单：

//......准备工作，根据图的信息初始化矩阵A和path (如上图)
for(int k=0; k<n ; k++){	//考虑以vk作为中转点
	for(int i=0; i<n; i++) {	//遍历整个矩阵，i为行号，j为列号
		for(int j=0; j<n; j++){
			if (A[i][j] > A[i][k]+A[k][j]){	//以vk为中转点的路径更短
                A[i][j] = A[i][k]+A[k][j];//更新最短路径长度
                path[i][j] = k;//中转点
            }
        }
    }
}

综上时间复杂度是O(N³)，空间复杂度是O(N²)。

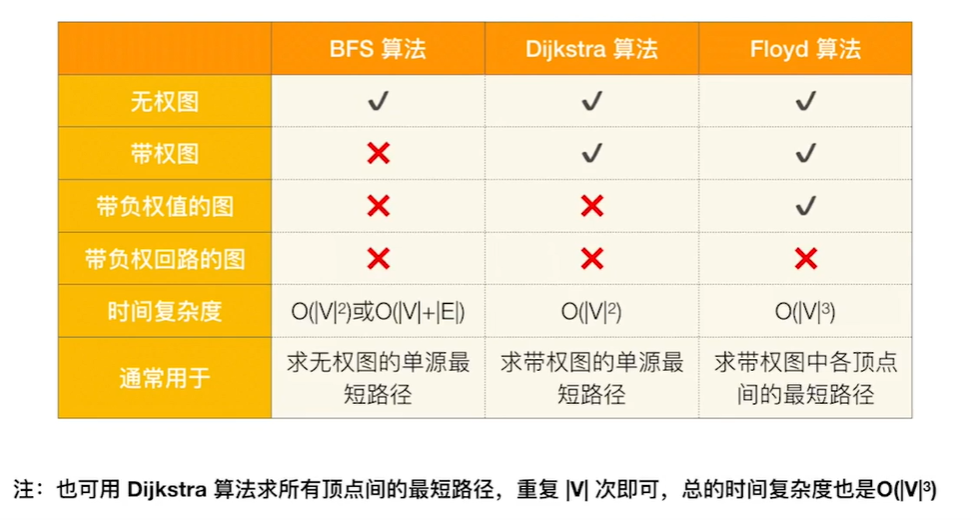
总结