欢迎来到博主的专栏——算法解析
博主ID：代码小豪

---

我们前面已经盘点了两种双指针算法的使用场景，现在来看看最常见的一种。

通常，我们遇到这种题型，即在一个数组中，找出任意两两数据，以达到某种条件（有时会要求三个）。博主在这里选择了比较典型的例子

LCR179、查找总价格为目标值的两个商品

解法一：暴力解法
两个for循环遍历出所有数据相加的结果，如果结果等于target，直接返回这个结果。

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        for (int i = 0; i < price.size(); i++)
        {
            for (int j = i + 1; j < price.size(); j++)
            {
                if (price[i] + price[j] == target)
                    return vector<int>({ price[i] ,price[j] });
            }
        }
        return vector<int>();
    }
};

实际上这种暴力解法也算是双指针，毕竟出现了两个下标i，j来指向数组中的数据。当然了这不是我们想要的双指针算法。因为效率太慢了

像这种在数组中找两个数据匹配的问题，暴力枚举肯定是有效的，只是时间复杂度太高，一旦数据项变多，那么可能就会出现超时的情况。

这里我们就要对枚举这个方法进行思考了。既然暴力枚举不可，那么有没改进的方法呢？当然有，这需要我们对条件进行思考了。

枚举这个方法不是不行，只是暴力枚举不太行，比如你的妈妈让你去买鱼，你会从五金店开始找吗？当然不会，因为直接到菜市场或者渔市上寻找会更加简单。如果我们在枚举的过程中，加上筛选掉不可能的选项，那么枚举的效率就会大幅提高。以此题为例，如果一个数大于两数相加的结果。那么这个数一定不会是需要加入枚举的选项，将其排除即可。这会提高我们的运行效率的当然，这个方法不是此题的解法。

我们先注意一下题目，看看这些数据有没有什么规律？

没错，这个数组是升序排序的。那么双指针可以对这个升序排序的数组做什么呢？
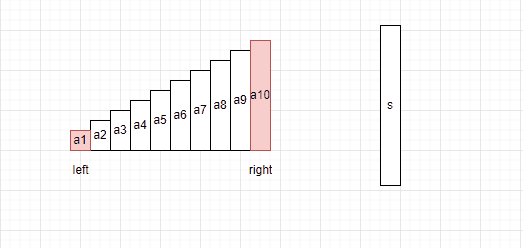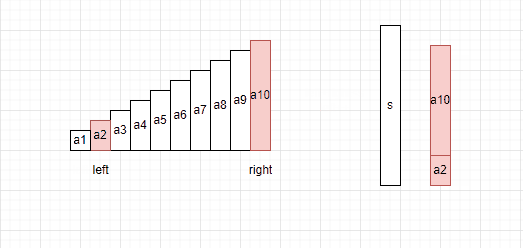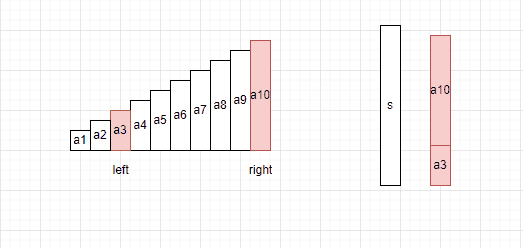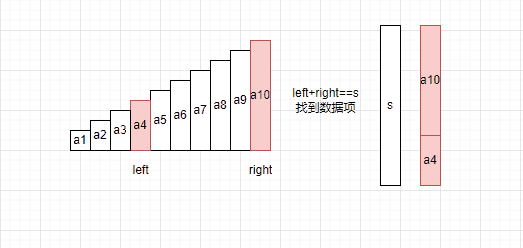
我们假设现在有一个由a1,a2,……a10十个升序的数据组成的数组。设目标值为s，现在取a3和a8求和，得到值s1，假设s1不等于s，那么s1的结果只能是大于或小于s。

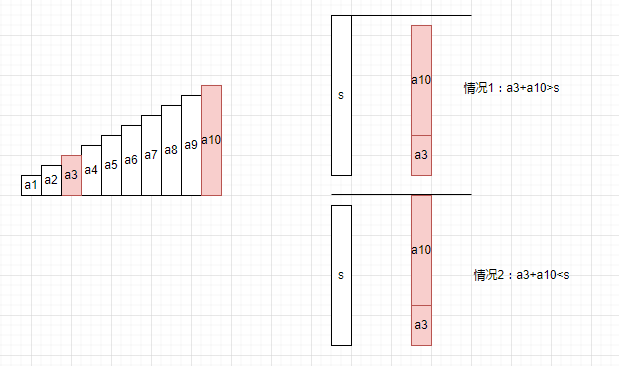
拿情况1举例，如果a3+a10>s，那么我们还需要判断a4+a10，a5+a10,……，a9+a10的结果吗？当然不用了，因为这是一个升序的数组，a3<a4<a5<…<a10，如果a3+a10都大于s了，那么a4+a10,a5+a10一定都是大于s的，因此我们不需要再枚举a3以后的数据与a10相加的结果是否等于s，而是应该判断a3+a9是否等于s。

拿情况2举例，同理，如果a3+a10<s了，那么a3+a9,a3+a8,a3+a7……都会小于s，因此也不用判断a10以前的数据与a3相加的结果是否等于s，而是要判断a3+a9是否等于s。

那么解决方法就很明确了，我们使用双指针算法来进行数据匹配，方法如下：
（1）指针left指向数组的起点，指针right指向数组的末尾
（2）如果left+right的结果<target，left++。
（3）如果left+right的结果>target，right–。

原理如下：
如果left+right的结果<target，这说明right之前的数据与left相加都会小于target，不再对right之前的数据与left进行匹配，而是让left++。
如果left+right的结果>target，这说明left之后的数据，与right相加都会大于target，不再对left之后的数据与right进行匹配，让right–。

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        int left = 0;//左指针
        int right = price.size() - 1;//右指针
        while (left < right)//数据匹配
        {
            if (price[left] + price[right] < target)//左右数据之和小于s
                left++;
            else if (price[left] + price[right] > target)//左右数据指针大于s
                right--;
            else//找到目标值
                return vector<int>{price[left], price[right]};
        }
        return vector<int>();//如果没找到，就返回空容器
    }
};

leetcode11——盛水最多的容器

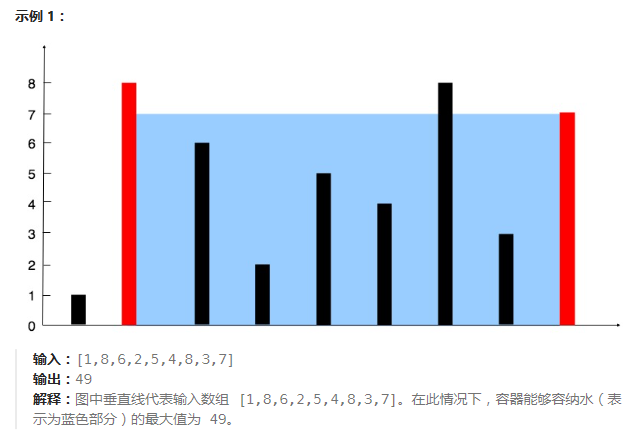
这道题看起来比上一道难多了，但实际上解题思路都是一样的。我们先来了解一下题目到底要求我们求什么？

假设现在有a1,a2,a3,a4,……a10十个数据组成的无序数组，任取两个数据

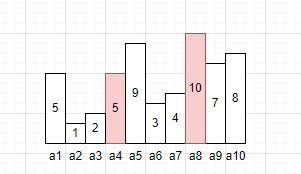
根据容器的体积公式v=s*h，其中h为两个数据的最小值，s为两个数据之间的距离。

在上例中，h为5，s=4.因此v=4*5=20。请牢牢记住这个公式，很重要。

解法1，暴力枚举。
暴力枚举的方法为，使用两个for循环，枚举数组中任意两两数组的组合的容积结果，然后取最大值。这个方法很挫，我就不把代码放出来了，反正也过不了leetcode的测试用例（因为超时）。

解法2，双指针算法
我们要知道的一点是，使用双指针算法来进行数据匹配的原理是，优化暴力枚举，通过排除一些不必要的数据，减少枚举的的结果，起到一个优化暴力枚举的作用，这也是博主为什么要再双指针解法之前提一嘴暴力枚举的原因。

那么我们来看看这道OJ题可以在哪个方面进行优化。还记得上道题是怎么做的吧?我们很好的利用了数组升序这一特点，找到了数据之间的特性。那么这个数组的数据有什么特性呢?

首先，我们先来找找这些数据的单调性，它们有序吗？没有，那么难道这道题就没有解法了吗？

当然不是，我们先来这些数据是什么？这些数据代表的是容器一边的高度，在这一组数据当中，高度是无序的，但是求容器的体积不单单需要考虑它的高度，也要考虑它的底。我们再来回顾一下容器的的体积公式

v=s*h

当h不变时，s变小，v就变小。如果h变小了，s也变小了，那么v还是变小。

诶，这不就是找到数据的单调性了吗？我们设一指针为left，指向数组的起始位置，一指针为right，指向数组的末尾位置，如果left和right逐渐靠近，那么s是逐步变小的，因为s=right-left。那么我们只需要判断，在left和right逐渐靠近时，容器的h是否变大了，因为h无论是不变还是变小，s变小了，体积都会变小。

解题步骤如下：
（1）让left指向数组的起始位置，right指向数组的末尾位置。
（2）比较left和right的数据，数据小的为容器的高度。记录一下当前的容积
（3）让较小数据的一方进行移动，比如left<right,则left++，left>right，则right–。
（4）如果有一出现了更大的高度，就要算出它的容积，并且与当前最大容积进行比较
（5）当left和right相遇时，返回当前最大容积。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0;
        int right = height.size() - 1;
        int max_high = min(height[left], height[right]);//求高度
        int max_area = max_high * (right - left);//当前最大容积

        while (left < right)
        {
            int high = min(height[left], height[right]);//较小的值作为容器的高
            if (high > max_high)
            {
                max_high = high;
                int new_area = high * (right - left);//计算新的面积是否是最大值
                max_area = max_area > new_area ? max_area : new_area;
            }
            if (height[left] > height[right])//哪边的数值小，就让那边的指针进行移动
                right--;
            else
                left++;
        }
        return max_area;
    }
};

leetcode611——有效三角形的个数

先来理解一下题目。
在一个数组当中，任取三个元素组合成一个三元组，这三个元素需要符合构成三角形的三边边长，计算一个数组中有多少个这种三元组。

我们先回顾一个中学知识。那就是三角型较小两边之和，必须大于最大的一条边。这是一个解题的关键。

解法1：
暴力枚举，枚举所有组合出来的三元组，并且判断这些三元组构成三角形的数量

解法2：
双指针算法。

实际上这道题的双指针算法比较取巧，因为这个数组本身是无序的，而博主先对整个数组进行排序，通常来说，我们在编写程序时，除非要求需要对数据进行修改，否则尽量不修改数据。只作判断。

当然，我们可以将数据拷贝到另外一个容器当中，对新拷贝容器就行排序，计算，然后返回计算结果，这样也不会对旧容器的数据进行修改。

将数组排成升序有什么好处，我们回顾一下判断三角形的要求

三角型较小两边之和，必须大于最大的一条边。

要知道一点是，如果我们要筛选三元组的数据，那么双指针一定是不够的，因为双指针最多指向两个数据，而三元组是由三个数据组成的。如果我们进行了升序的排序，可以得到这么一个结果。

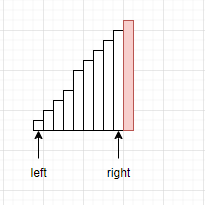
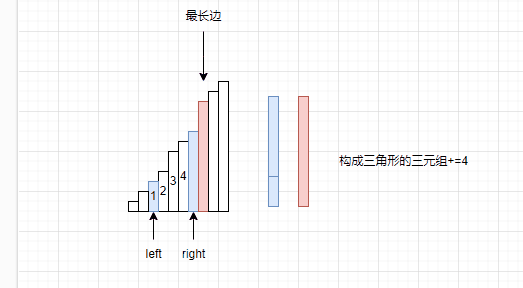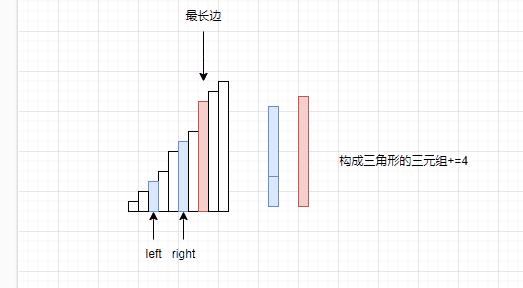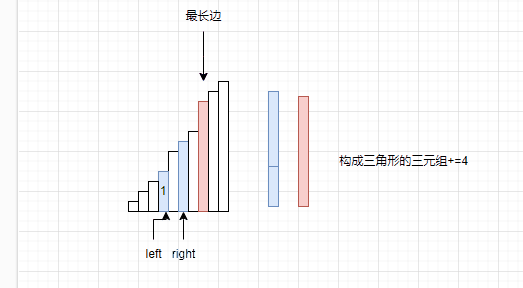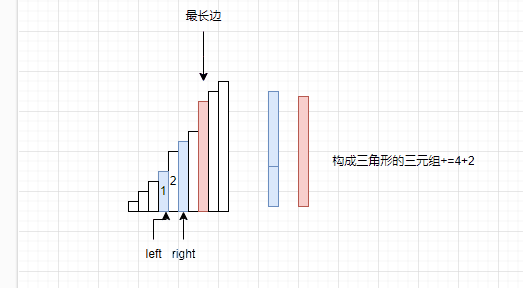
没错，我们找到了最长的一边，因为数据已经排成升序了，数据从后向前是依次递减的，因此，我们可以假设某条边是最长边。

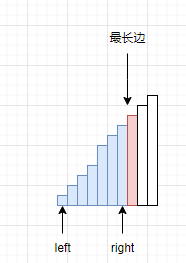
因为该数是最长边，因此与它组成三元组的其他两条边都在区间[left,right]以内。因为既然选择红色这边作为最长边，那么红色之后的数据比红色长，那么显然是不对的，因为选取了红色作为最长边。

那么现在已经解决了一个问题了，知道了最长边是多少，但是剩下两个边长该如何选取呢？
其实在图中已经给出答案了，我们假设right指向的是次长的边，left指向最短边。OK，那么解决方式已经非常简单了，因为left+right如果大于最大边，那么就不用计算left之后的数据与right组合的结果了，因为升序的原因，left之后的数据都会比left大。直接让构成三元组的个数+=right-left。之后让right–。

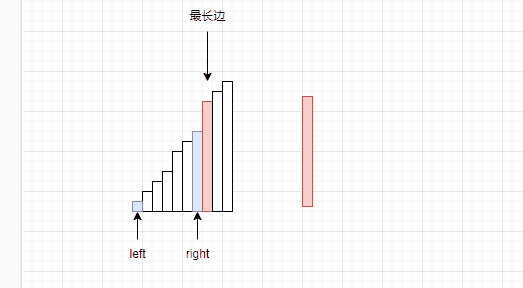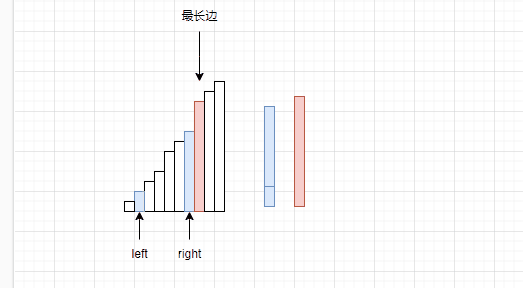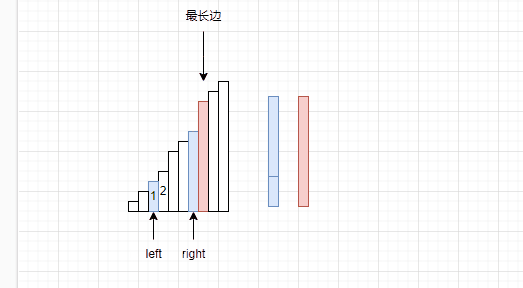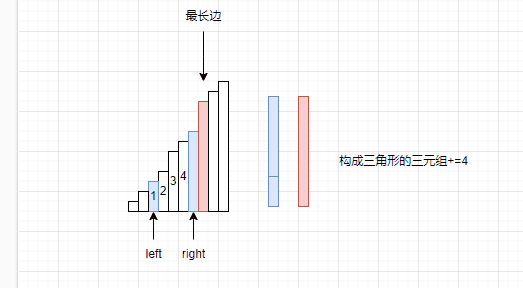
为什么要让right–呢？因为我们已经明确了这个规则，最长边，次长边不动，计算最短边和次长边之和时候大于最长边。但是次长边是可以变化的啊，因此要让right–。

如果right与left相遇了，那就枚举完当前区间与最长边构成三角形的所有情况，让其他的数据做最长边。

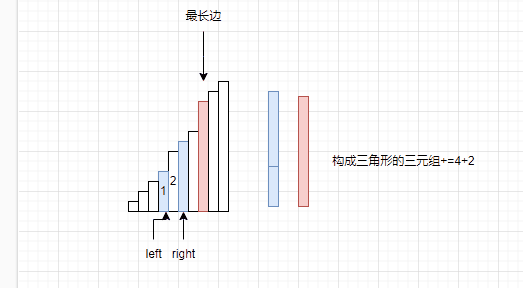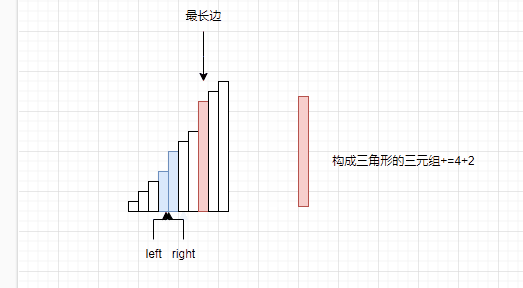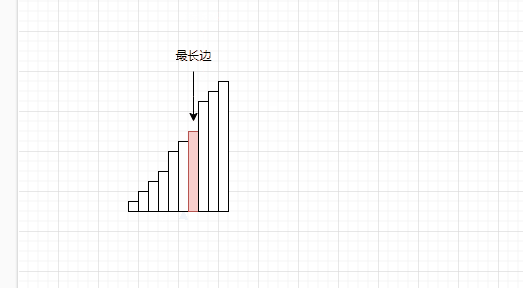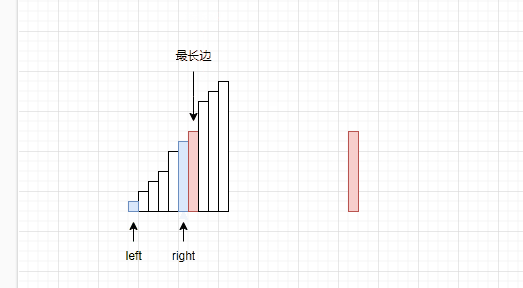
（1）我们设最长边为max_edge，让left指向数组的起始位置，right指向max_edge的前一个数据。
（2）计算left+right>max_edge的结果，若left+right>max_edge,就计算[left,right）之间的数据个数，反之，left++
（3）计算完[left,right)之间的个数后，让right–，重复第二步
（4）如果left和right相遇了，就让max_edge–，重复第1步
（5）如果max_edge来到了数组的起始位置，那么枚举结束

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        sort(nums.begin(), nums.end());//将数组排成升序
        int max_edge = nums.size() - 1;//最长边
        int count = 0;//构成三角形的三元组计数

        while (max_edge > 1)
        {
            int left = 0;
            int right = max_edge - 1;
            while (left < right)
            {
                if (nums[left] + nums[right] > nums[max_edge])//较小两边之后大于第三边
                {
                    count += right - left;
                    right--;
                }
                else
                    left++;
            }
            max_edge--;
        }
        return count;
    }
};