[数据结构]-快速排序

学习快排的基础

不想自己推导时间复杂度或者了解随机化的合理性,可以忽视下面这一条.

推导时间复杂度的方法:主定理
随机化算法—数学基础:概率统计

`QuickSort`

快速排序:
1962年,Tony Hoare发明了这种如此高效实用的强大排序算法

分治法的体现:Divide and Conquer
原地排序,不需要额外申请空间.
实用.

快速排序分析

快速排序采用了分治思想.
其基本思想:

Divide: 找到一个主元Key,将原数组划分(Partition)成两个子数组Subarray.
满足左子数组数据小于等于Key,右子树组数据大于Key.
Conquer:递归处理两个子数组,对两个子数组进行快速排序.
Combine:合并-----快速排序不需要这一步,不重要.
先看第一步:
Divide:封装一个函数Partition,划分子程序.
线性时间复杂度: $\Theta(n)$
对于子数组 $A [p ... q]$

PARTITION(A, p, q) 
	x = A[p] 
	i = p
	for j = p + 1 to q 
	if A[j] <= x 
		i = i + 1 
		exchange A[i] with A[j] 
exchange A[p] with A[i] 
return i

伪代码能看明白吗?

+------------------------+
|p|  <=X  |i  >x  |j   |q|
+------------------------+

选定一个元素为枢轴,这里先考虑选择数组区间 $A [p ... q]$ 的第一个元素A[p].–其它选法暂时别考虑
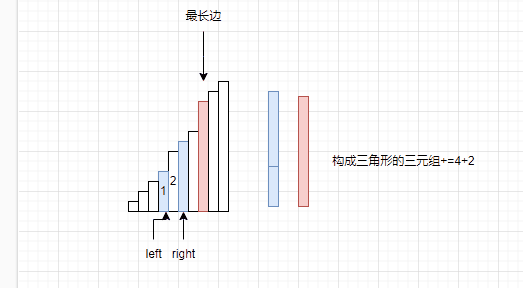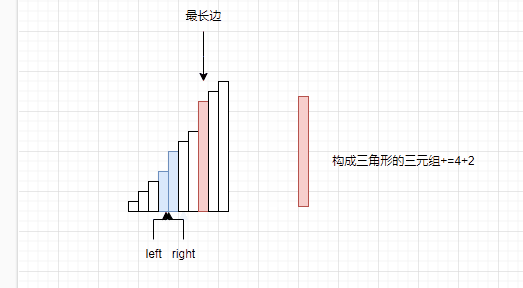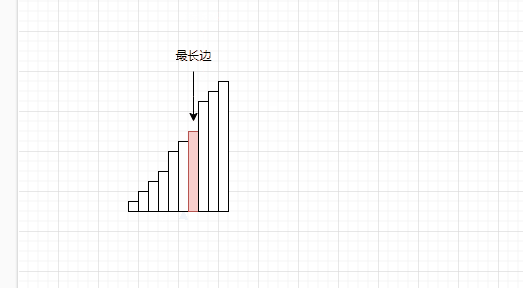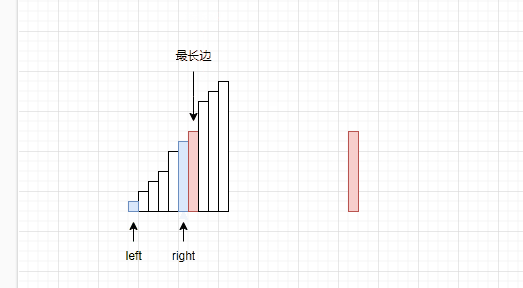
接下来要用i,j变量来维护区间了,这一过程本质上是将枢轴A[p]放到正确的位置
先看中间过程 $[i ... j]$ 区间,很显然 $i$ 为分割线–左边<=x,右边>x.
$j$ —扫描数据,遍历数组将遇见的元素先判断放到对应区间.
给定[10, 7, 8, 9, 1, 5],自行画图分析一下伪代码的过程吧.
在这里插入图片描述

下面我们用简单的python程序实现一下

def swap(A,i,j):
    A[i], A[j] = A[j], A[i]
def Partition(A,p,q):
    x = A[p]
    i = p
    j = i + 1
    while j<q:
        if A[j]<=x:
            i += 1
            swap(A,i,j)
        j+=1
    swap(A,p,i)
    return i

快速排序的伪代码

QuickSort(A, p, q)
    if p < q then
        r = Partition(A, p, q)//
        QuickSort(A, p, r - 1)
        QuickSort(A, r + 1, q)

快速排序只有分,治,没有合并部分.
回忆:归并排序先等分数组,不断递归,最后核心部分是合并两数组.快速排序则是第一步分区间重要,单趟快排原理搞明白了,后面的划分区间递归小菜一碟.
解释上面伪代码:

递归处理基线问题很重要,弄不好边界,对于特定输出很容易导致栈溢出.
画出递归树图—p<q时可以递归.
否则,直接结束调用向上返回,别进递归了,StackOverFlow.
Partition函数要返回分割两区间的下标以便于后续分左右子区间调用快速排序.
用 $r$ 分割原区间 $[p, q]$ 为 $[p, r - 1]$ 和 $[r + 1, q]$ ,递归快排.

还是python代码

def QuickSort(A,p,q):
    if p<q:
        r = Partition(A,p,q)
        QuickSort(A,p,r-1)
        QuickSort(A,r+1,q)

不知道为什么我总有一种不安全感,有一种栈溢出的美.
鲁迅曾经说过:栈分配的内存空间是有限的,递归太深就抛异常了.
不急,先写到快速排序题
直接用C手搓快排,然后提交.

void swap(int *x,int *y)
{
    int tmp = *x;
    *x = *y;
    *y = tmp;
}
int partition(int *nums,int left,int right)
{
    int x = nums[left];
    int i = left;
    for(int j = left + 1;j<right;j++)
    {
        if(nums[j]<x)
        {
            i++;
            swap(nums+i,nums+j);
        }
    }
    swap(nums+left,nums+i);
    return i;
}
void QuickSort(int *nums,int left,int right)
{
    if(left<right)
    {
        int keyi = partition(nums,left,right);
        QuickSort(nums,left,keyi);
        QuickSort(nums,keyi+1,right);
    }
}
int* sortArray(int* nums, int numsSize, int* returnSize) {
    *returnSize = numsSize;
    QuickSort(nums,0,numsSize);
    return nums;
}

竟然超时了:快速排序不是号称时间复杂度 $\Theta(nlog_2n)$ 吗?
对于特定的输入,当给定数组接近有序或者本身有序,快速排序效率降低-原始的快速排序解决不了这种特定输入.
回忆:Insertion Sort(插入排序)—时间复杂度: $\Theta(n^2)$ .
快速排序面对这种输入序列,效率和插排一样也是 $\Theta(n^2)$ .
不同的是插入排序越接近有序序列,效率越高.而快排则反过来.

# 用这组测试用例测试一下前面的python代码
list = [5]*10000
QuickSort(list,0,len(list))
print(list)

RecursionError: maximum recursion depth exceeded 递归太深,python也抛异常了.
每次快排不是等分的,理想情况每次完美均分,那么画它的递归树就是一棵完全二叉树 $\Theta(log_2n)$ ,每趟时间复杂度 $\Theta(n)$ .两者相乘时间复杂度 $\Theta(nlog_2n)$ .—估计法,此法不严谨.
快排厉害的地方在于每次单趟快排,哪怕不均匀分配,运行效率已然很好.-------稍后会在时间复杂度处给出证明.
若均匀等分时间复杂度 $\Theta(log_2n)$ ,那么按照1:9;2:8,3:7划分数组区间这些比例同样很好,即平均来看时间复杂度也是 $\Theta(log_2n)$ .
只有大量单趟快排出现一遍倒的情况,对于这种特定的输入,快排时间复杂度才会退化为上面的糟糕情况.

Java实现朴素快速排序

前面C/Python写了一遍未优化的快速排序.
这种快速排序采用了双指针的算法技巧,我一般称为"前后指针法."
上面"前后指针"的快速排序处理重复元素效率较低,快排创始人霍尔大佬的写法处理重复元素的情况相对较好.

霍尔法

霍尔法还是采用双指针算法
partition函数实现方式不同,其余相同
左右指针(对撞指针)：设置两个指针，左指针从左到右遍历，右指针从右到左遍历。
交换元素：

左指针从左向右移动，直到找到一个大于或等于枢轴的元素。
右指针从右向左移动，直到找到一个小于或等于枢轴的元素。
交换这两个元素，并继续移动指针，直到左指针和右指针相撞。
初学此排序时,最先学的就是霍尔法了,不过此法坑点极多,极容易写错
请先看代码:

private static int partition(int[] array, int left, int right) {
        //主元下标
        int keyIndex = left;
        int x = array[left];
        while(left<right)
        {
            while(left<right&&array[right]>=x)
            {
                right--;
            }
            //array[right]<x
            while(left<right&&array[left]<=x)
            {
                left++;
            }
            swap(array,left,right);
        }
        swap(array,keyIndex,left);
        return left;
    }

int keyIndex = left;取子数组最左边的数为主元—可见该写法依赖输入序列,是原始的快速排序.
while(left<right)这个最外层循环,对撞指针,循环结束条件left==right
while(left<right&&array[right]>=x) 和 while(left<right&&array[left]<=x)
为什么内层两循环必须left<right必须存在?由于循环内要调整数组下标,肯定在循环条件上加以限制.否则可能存在数组越界的情况.
比如:[1,2,3,4,5,6],right->6,它会从右往左找比1小的数,然后一骑绝尘飞出数组数组越界了
注意6,&&右边均是取了等号的,只保留一个等号或者不取等可以吗?
假设 while(left<right&&array[right]>x) 和 while(left<right&&array[left]<x).
两个循环体条件都没去等号,可能发生死循环吗?
答案是肯定的,这个值就是array[right]==array[left]==x
举例[3,3,3,3],对于这个数组.left与right均有效,但是它们不会进内部循环.
后面交换了,还是原先的值依然死循环.
再假设 while(left<right&&array[right]>x) 和 while(left<right&&array[left]<=x).
只保留一个取等可以吗?
答案:也不可以!
举例:left,right重叠,但right本身没动过,自身交换陷入死循环.
[110, 100, 0] :right->0,left->110;right不满足移动条件原地不动,left一路右移,与right重叠.执行swap,自己与自己交换没用.再次循环,right不动,left也不动了,至此死循环了.
为什么先移动right,后移动left?
首先,请看
$r i g h t :$ 寻找 $<= x$ 的元素.
$l e f t :$ 寻找 $>= x$ 的元素.
进行交换分区.
用反证法:
假设先移动left再移动right.
无论最终一步是left走还是right走.最终指向位置一定 $>= x$ .最终与x交换,达不到分区的效果.
举例:[1,3,-1,5,7]left先走,先走到5处,right走到5处就两者相遇,5与x交换.
数组变为[5,3,-1,1,7],最左边的元素5不满足 $<= x$ ,分区失败.
因此,从这个角度看,right先走非常合理.

以下是Java代码完整实现:

 public static void quickSort(int[] array)
    {
        quick(array,0,array.length-1);
    }
    private static void quick(int[] array,int left,int right)
    {
        if(left<right) {
            int pivot = partition(array, left, right);
            quick(array,left,pivot-1);
            quick(array,pivot+1,right);
        }
    }
    private static void swap(int[] array,int i,int j)
    {
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }
    private static int partition(int[] array, int left, int right) {
        //主元下标
        int keyIndex = left;
        int x = array[left];
        while(left<right)
        {
            while(left<right&&array[right]>=x)
            {
                right--;
            }
            //array[right]<x
            while(left<right&&array[left]<=x)
            {
                left++;
            }
            swap(array,left,right);
        }
        swap(array,keyIndex,left);
        return left;
    }

挖坑法

 private static int partition(int[] array, int left, int right) {
        //先给左边挖个坑
        int key = array[left];
        //记录最初的坑点
        int i = left;
        while(left<right)
        {
            while(left<right&&array[right]>=key)
            {
                right--;
            }
            //右边挖坑填左边
            array[left]=array[right];
            //array[right]<x
            while(left<right&&array[left]<=key)
            {
                left++;
            }
            //左边挖坑填右边
            array[right]=array[left];
        }
        //填最初的坑.
        array[left]=key;
        return left;
    }

前后指针法请自行实现

时间复杂度分析

对于这组[5,5,.....5]-->10000个5的数组列表.面对重复元素,若每次只取第一个元素为枢轴,那么每次单趟遍历一遍数组然后分割数组,分割结果:右数组始终为空数组.
快速排序处理本身有序的数组会非常糟糕,这说明原始的快速排序依赖输入序列.

最坏情况

数组一边倒:对于输入序列[1,2,...n]
$T (n) = T (n - 1) + T (0) + n$
在这里插入图片描述
已知 $\theta(1)$
$\theta(\sum_0^nck+T(0)) =\theta(n^2)$
如果一直不均等分配,那么快速排序很低效的.

最佳情况

均匀二等分最佳
$\theta(n)$
符号主定理第二种情况: $\theta(nlgn)$
$CS中:lgn ☞log_2n$
也可以画递归树.

平均情况

若不均匀分配呢?
比如不是按照最佳5:5比例,而是始终按照1:9比例分配呢?
那么它接近最佳情况还是最糟情况呢?
接近最佳情况:这就是快速排序的魅力时刻
时间复杂度: $\Theta(nlgn)$
证明过程仅靠作者现有工具描述太过粗糙,递归树和放缩法可以粗略得出结论.
详见算法导论书籍以及有关课程

随机化的快速排序

随机化快排是快速排序的优化版本.
严格推导极其依赖概率统计的相关知识,若是有数学基础,请自行查阅算法导论阅读.
快排对于特定序列表现得很糟糕,随机化算法就是想让快速排序不依赖输入序列,快排效率取决随机化的结果.我起初觉得随机化太依赖运气,直到我懵懵地看过推导,才发现其中精妙无穷.

优化方案有很多,先说随机化的三数取中法,然后减少递归深度的快速排序混入插入排序
三数取中法:
每次比较[left...right]与中间下标A[mid],取中位数,返回下标.

private static final int getMiddleNum(int[] arr,int left,int right)
    {
        int mid = (left+right)/2;
        if(arr[left]<arr[right])
        {
            if(arr[mid]<arr[left])
            {
                return left;
            }
            else if(arr[mid]<arr[right])
            {
                return mid;
            }
            else
            {
                return right;
            }
        } else//arr[left]>=arr[right]
        {
            if(arr[mid]<arr[right])
            {
                return right;
            }
            else if(arr[mid]<arr[left])
            {
                return mid;
            }
            else
            {
                return left;
            }
        }
    }
    private static void quick(int[] array,int left,int right)
    {
        if(left<right) {
            int mid = getMiddleNum(array,left,right);
            //将中位数的值与左区间交换.
            swap(array,left,mid);
            int pivot = partition(array, left, right);
            quick(array,left,pivot-1);
            quick(array,pivot+1,right);
        }
    }

插入排序优化
快速排序分而治之,导致后续子数组的数据规模越来越小.换言之,相比原来大的数组,小数组越来越有序了.
面对减小规模且接近有序的数组区间,插入排序算法可以说是最佳选择.
所以我们另起一个分支,设定数据规模,小于等于时采用插入排序,大于则采用递归快速排序.

//插入排序
    private static void insertSort(int[] array,int left ,int right)
    {
        for(int i=left+1;i<=right;i++)
        {
            int tmp=array[i];
            int j = i-1;
            while(j>=0&&array[j]>=tmp)
            {
                array[j+1]=array[j];
                j--;
            }
            array[j+1]=tmp;
        }
    }

 private static final int MAX_LENGTH_INSERT_SORT = 7;//满足插入排序的临界规模
 private static void quick(int[] array,int left,int right) {
        if (left < right) {
            if(right - left + 1<10)
            {
                insertSort(array,left,right);
                return ;
            }
            int mid = getMiddleNum(array, left, right);
            swap(array, left, mid);
            int pivot = partition(array, left, right);
            quick(array, left, pivot - 1);
            quick(array, pivot + 1, right);
        }
    }

可以通过了
不过自己写的快排效率绷不住,感兴趣可以翻一下JavaArrays.sort方法的源码.

补充非递归实现快排.

利用栈的特性.
原因:
栈天然模拟递归.栈的LIFO特性确保了每次处理的子数组顺序与递归调用时保持一致。
画递归树图,你会发现这和递归处理顺序一模一样.
栈:简单,而且利用栈避免递归带来深度过深的栈溢出问题.

下面if(pivot>left+1),你可能感到困惑.
别急,这等同于递归的基线条件:两个及以上元素的区间才能够进行后续操作.
栈存储数对:区间端点下标.将一对数进行入栈操作,进行partition分割.
先处理右边的子数组，再处理左边的子数组:这是栈LIFO的体现.
终止条件:栈为空,那么迭代快排的条件是栈不为空.

    public static void quick2(int[] array,int left,int right)
    {
        Deque<Integer> stack = new ArrayDeque<>();
        int pivot = partition(array,left,right);
        if(pivot>left+1) {
            stack.push(left);
            stack.push(pivot - 1);
        }
        if(pivot<right-1)
        {
            stack.push(pivot+1);
            stack.push(right);
        }
        while(!stack.isEmpty())
        {
            right = stack.pop();
            left = stack.pop();
            pivot = partition(array,left,right);
            if(pivot>left+1) {
                stack.push(left);
                stack.push(pivot - 1);
            }
            if(pivot<right-1)
            {
                stack.push(pivot+1);
                stack.push(right);
            }
        }
    }