0 前言
part1讨论了集成过程中遇到的挑战以及幂等事件处理的作用。解决集成问题之后,我们需要反思事件检索的问题。我们的经验教训表明,将事件检索与事件处理解耦至关重要。
1 事件处理与请求/响应 API 紧耦合
part1讨论了将请求/响应 API 集成到事件驱动微服务中时,由于基于请求/响应的通信,导致紧耦合。单个事件的处理速度取决于请求/响应 API 及其响应时间,因为事件处理会阻塞直到收到响应。
像我们在part1中使用的简单事件循环实现或 AWS SQS Java Messaging Library 中的工作示例,会顺序处理事件。
不推荐这种方法,因为整体处理时间是所有单个处理时间的总和。
2 并发处理事件
幸运的是,像 Spring Cloud AWS 这种库提供支持并发处理事件的更高效实现。属性 ALWAYS_POLL_MAX_MESSAGES 的行为在下图概述:并发事件处理
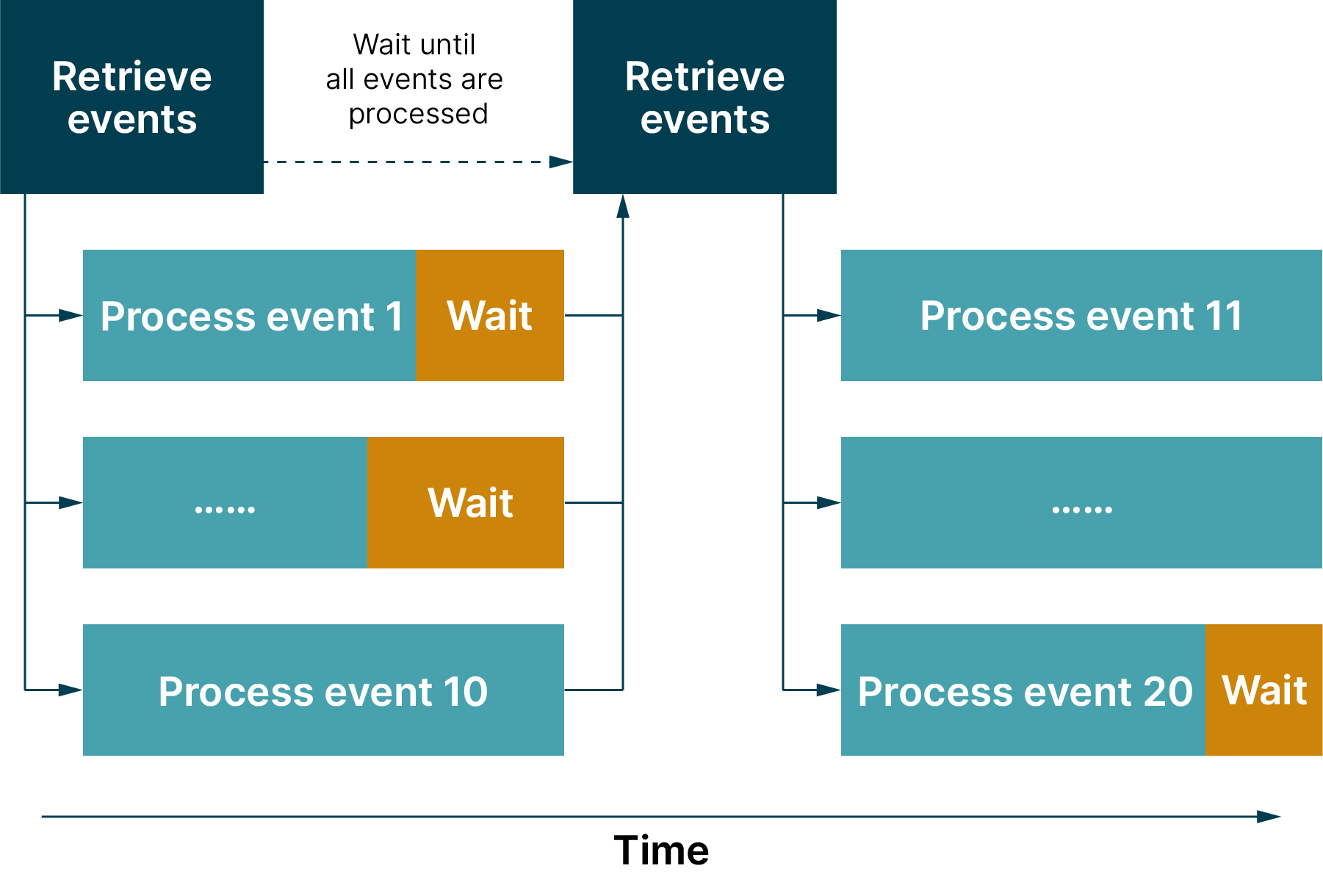
检索到一批事件后,每个事件在一个单独的线程中并发处理。当所有线程完成处理后,将检索下一批事件。由于基于请求/响应的通信导致的紧耦合,可能使事件处理速度不同。较快的线程会在较慢的线程处理事件时处于等待状态。因此,一批事件的处理时间对应于处理最慢的事件的时间。
当事件顺序不重要时,并发处理可以是一个合理的默认设置。但根据经验,某些情况下,事件处理可进一步优化。当单个事件的处理时间差异较大时,线程可能长时间处于等待状态。
如集成了一个性能波动较大的请求/响应 API。平均而言,该 API 在 0.5s 后响应。但第 95 百分位和第 99 百分位值经常分别为 1.5s 和超过 10s。在这种并发事件处理方式中,由于响应缓慢的 API,线程经常会等待几s,然后才能处理新事件。
3 将事件检索与事件处理解耦
即可进一步优化事件处理。这样,处理时间较长的单个事件不会减慢其他事件的处理速度。Spring Cloud AWS 提供了 FIXED_HIGH_THROUGHPUT 属性,展示了这种解耦可能的实现方式。
具体描述如下。详细信息可在文档中找到。
解耦的事件处理策略:
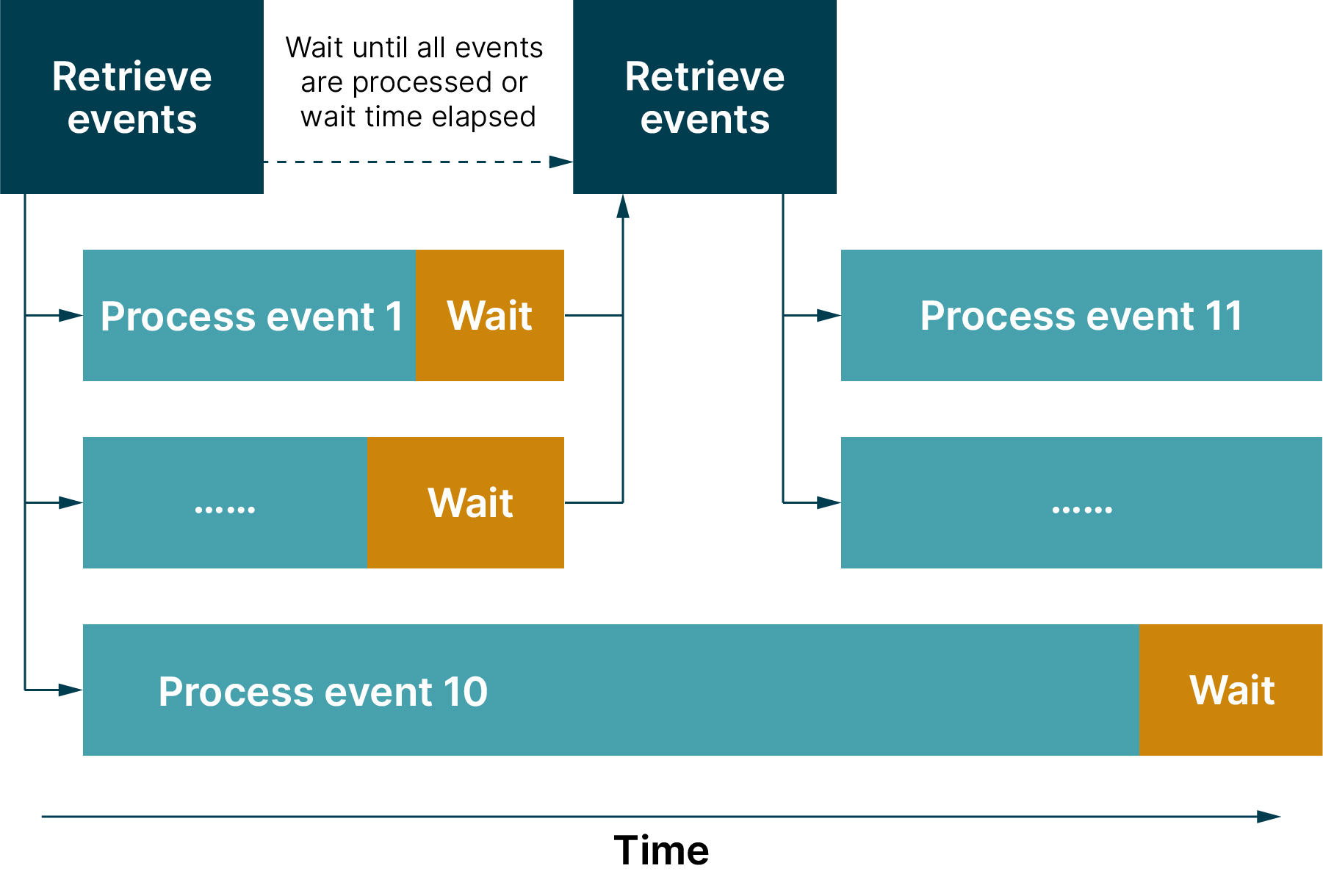
为此,定义一个额外属性,用于在两次事件检索之间的最大等待时间。当所有事件已处理完毕或等待时间已过期时,将检索新事件。若在等待时间过期后,如一个事件仍未处理完毕,则会提前接收九个新事件,并可以开始处理。这意味着这九个线程不会等到最后一个事件处理完毕后才开始工作。
根据经验,如果等待时间和其他参数配置得当,解耦可提高单个线程的利用率。一个可能缺点,由于事件往往以更频繁但较小批次的方式被检索,因此可能增加成本。因此,了解 API 性能特征,对于在并发和解耦事件处理之间做出选择至关重要。
4 结论
当你将事件驱动微服务与请求/响应 API 集成时,会引入紧耦合。请求/响应 API 的性能特征很重要,因为它们有助于你在并发和解耦事件处理之间做出选择。
本文重点讨论了请求/响应 API 的请求时间性能及其如何影响事件驱动微服务的性能。
关注我,紧跟本系列专栏文章,咱们下篇再续!
作者简介:魔都架构师,多家大厂后端一线研发经验,在分布式系统设计、数据平台架构和AI应用开发等领域都有丰富实践经验。
各大技术社区头部专家博主。具有丰富的引领团队经验,深厚业务架构和解决方案的积累。
负责:
中央/分销预订系统性能优化
活动&券等营销中台建设
交易平台及数据中台等架构和开发设计
车联网核心平台-物联网连接平台、大数据平台架构设计及优化
LLM Agent应用开发
区块链应用开发
大数据开发挖掘经验
推荐系统项目
目前主攻市级软件项目设计、构建服务全社会的应用系统。
参考:
- 编程严选网
本文由博客一文多发平台 OpenWrite 发布!