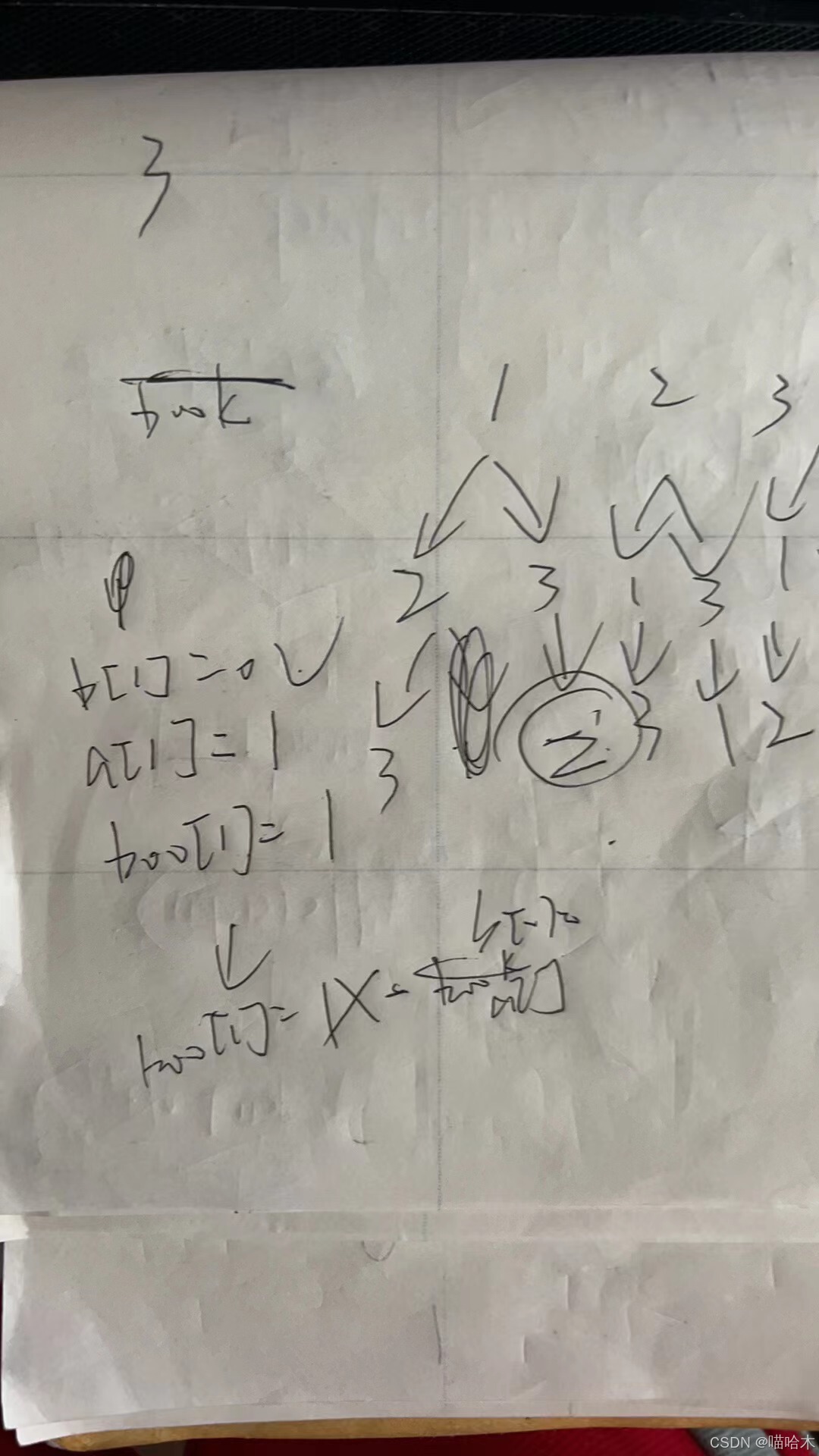
输入一个自然数N（1<=N<=9），从小到大输出用1~N组成的所有排列，也就说全排列。例如输入3则输出
123
132
213
231
312
321

输入格式:

输入一个自然数N（1<=N<=9）

输出格式:

N的全排列，每行一个

限制:

每个测试点1秒

样例 1 :

输入:
2

输出:
12
21

样例 2 :

输入:
3

输出:
123
132
213
231
312
321

#include<stdio.h>

int n,book[10],a[101];

void dfs(int step){
	
	int i;
	
	if(step == n+1){
      for(i = 1;i <= n;i ++)
          printf("%d ",a[i]);
	    printf("\n");
      return;
    }
	
    for(i = 1;i <= n;i ++){
    	
    	if(book[i] == 0){
    	   a[step] = i;
    	   book[i] = 1;
		   dfs(step + 1);
		   book[i] = 0;
		}
		
	}
	
	return;
    
}

int main(){
	int i;
	scanf("%d",&n);
	for(i = 1;i <= n;i ++){
		a[i] = 0;
	}
	dfs(1);
	return 0;
}

i 原本被搞为全局变量

book[i] = 1;没有

if(step == n+1){
      for(i = 1;i <= n;i ++)
          printf("%d ",a[i]);
	    printf("\n");
      return;
    }

放在了for循环后面

错误类型还是一样的，还是要多练。另外就是变量值这里，举例子的时候可能也只是逻辑上的，而忽视了具体的，最好把变量的值的变化写下来或者使用IDEL的debug功能