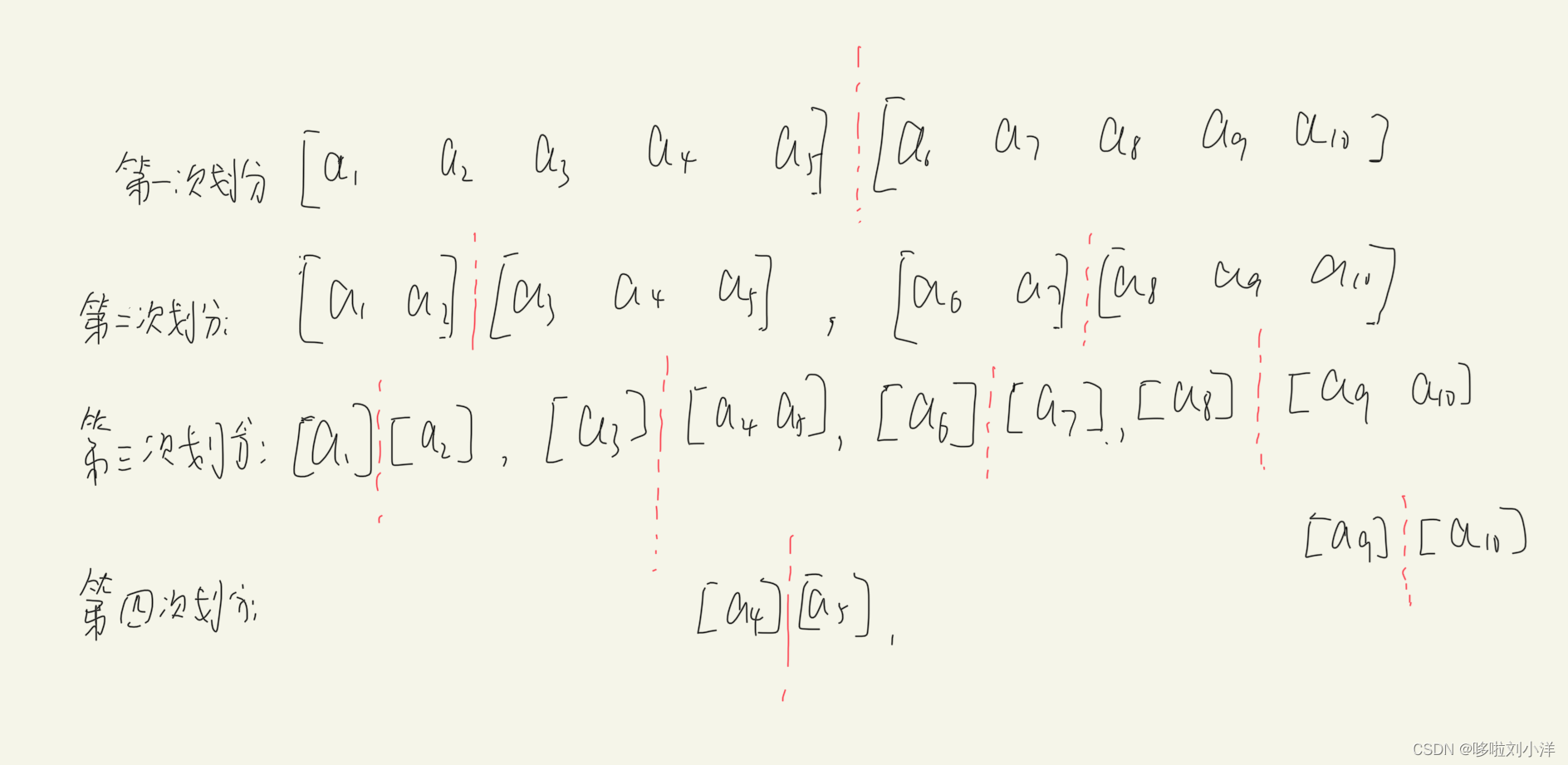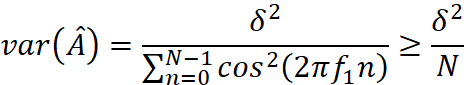回溯是递归的副产品，只要有递归就会有回溯。

回溯算法，不是一个高效的算法，纯暴力算法，实际上是递归算法的一部分，最多再剪枝⼀下。

回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，穷举过程就是遍历一颗多叉树的过程。

回溯算法能解决几种问题：

1、全排列。给定一个没有重复数字的序列，返回其所有可能的全排列。

2、部分棋盘问题，n皇后问题，解数独等

3、切割。一个字符串有几种切割的方式

4、子集。一个字符串或是N个数的集合里有多少符合条件的子集

5、组合问题。N个数里面按一定规则找出k个数的组合。例如力扣https://leetcode.cn/problems/4sjJUc/有重复元素集合的组合

回溯法：通常被抽象为一个n叉树，横方向是for循环,纵方向递归

List<Object> result;

/**
* 回溯代码框架
*/
void backtrack(path,chooseList){
     //满足结束条件
     if(isOver){
        result.add(path);
        return;
     }

     for(choose:chooseList){
        //做选择
        backtrack(path,choose);
        //撤销选择
     }
}



/**
*多叉树
*/
void traceTree(TreeNode root){
     if( root == null){
         return;
     }
     for(TreeNode child: root.children){
         raceTree(child);
     }

}

回溯法中递归函数参数很难⼀次性确定下来，⼀般先写逻辑，需要什么参数，填什么参数。