作者:~小明学编程
文章专栏:Java数据结构
格言:目之所及皆为回忆,心之所想皆为过往
快速排序和归并排序作为排序中的两个重点,也是面试中最常考的两个知识点,这里带大家详解的了解这两个排序。
目录
快速排序
原理
填坑法
代码
Hoare 法
优化
在待排序区间选择一个基准值
设置阈值
非递归法
性能
归并排序
原理
代码
递归法
非递归法
性能
总结对比
快速排序
原理
快速排序的思想是这样的:
填坑法
1.首先我们需要从待排序区间选择一个数,作为基准值(pivot),这里我们常用的就是那我们的最左边的数当作基准,将其挖走。
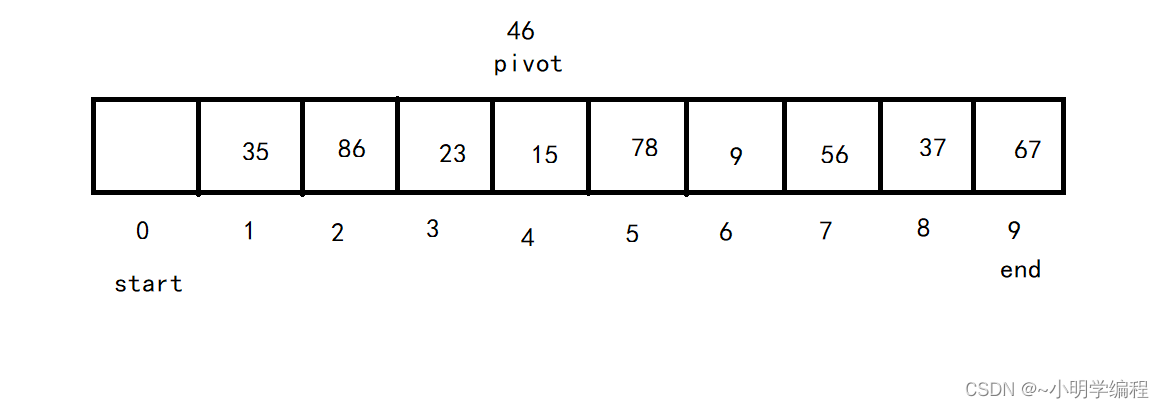
2. Partition: 遍历整个待排序区间,我们将左边下标的位置定义为start,将右边下标的位置记作end,因为我们的最左边被挖走了所以我们要想办法将这个坑给填了,先是从右边向左找也就是end的位置开始找,找一个比基准(pivot)小的数然后将其填在我们的start的位置。
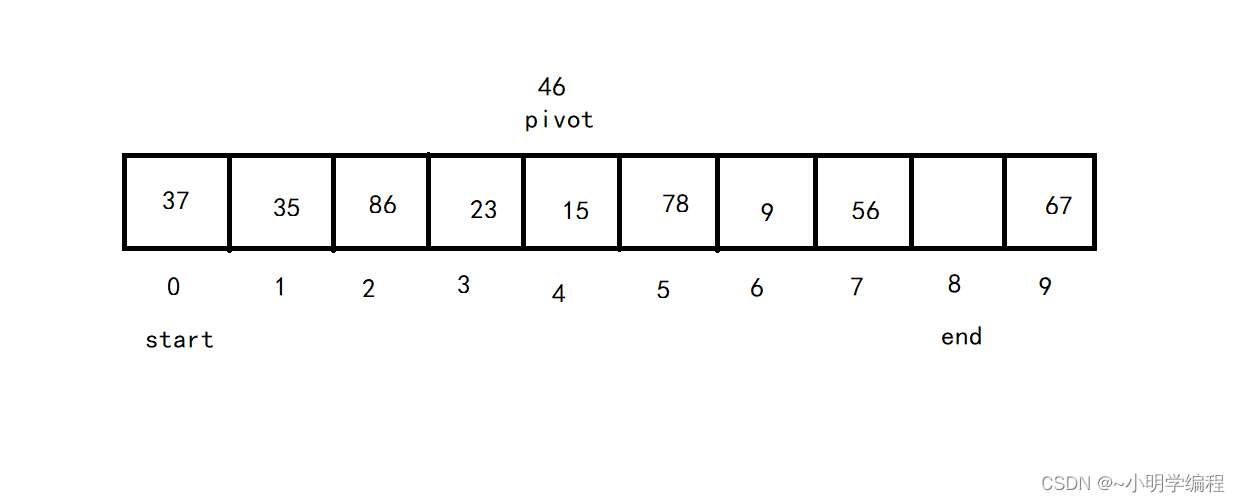
接着我们从左向右找也就是start的位置开始找,找一个比基准(pivot)大的数将其填在end的坑中,
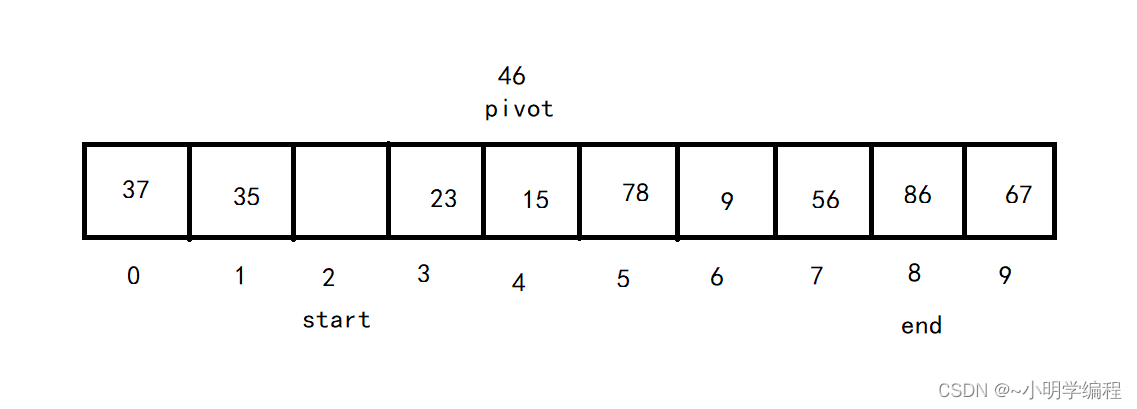
然后循环上述的过程直至start==end,
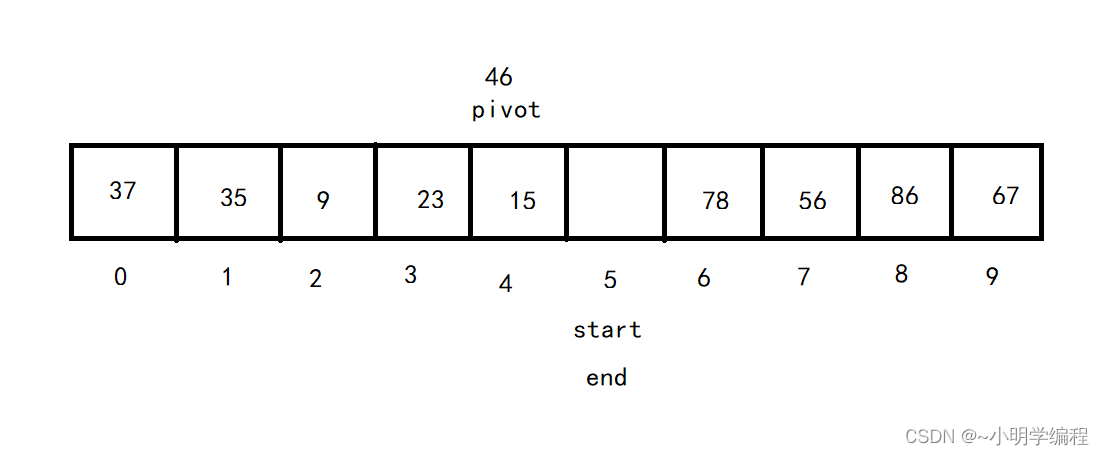
然后我们在strat的位置将我们的基准pivot给填上去。
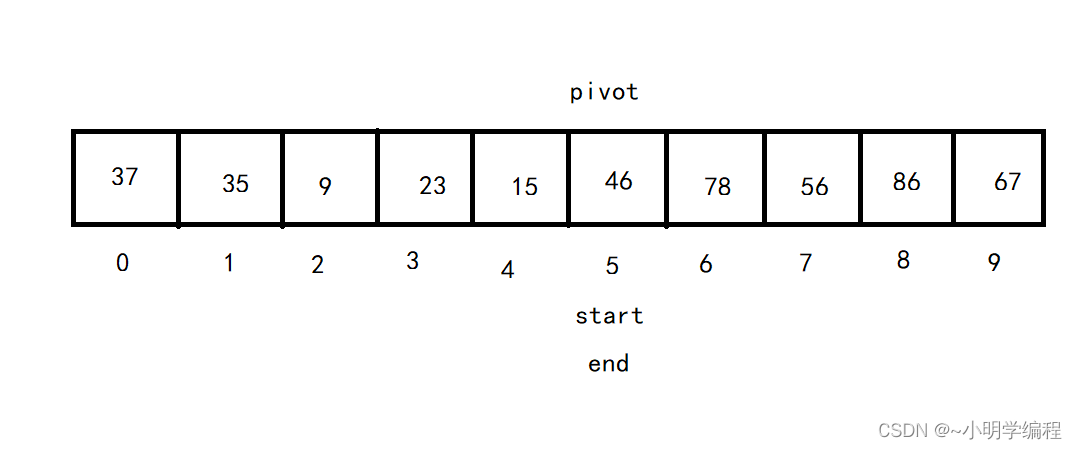
这时我们可以看到pivot的左边的数都小于基准,右边的数都大于基准,就完成了我们初步的排序。
3.采用分治思想,对基准的左右两个小区间按照同样的方式处理,直到start>end。
代码
public static void quickSort(int[] array) {
quick(array,0, array.length-1);
}
public static void quick(int[] array,int left,int right) {
if (left>right) {
return;
}
int pivot = partition(array,left,right);
quick(array,left,pivot-1);
quick(array,pivot+1,right);
}
public static int partition(int[] array,int start,int end) {
int pivot = array[start];
while (start<end) {
while (array[end]>=pivot && start<end) {
end--;
}
array[start] = array[end];
while (array[start]<=pivot && start<end) {
start++;
}
array[end] = array[start];
}
array[start] = pivot;
return start;
}Hoare 法
Hoare 法的思想是:
1.首先我们需要从待排序区间选择一个数,作为基准值(pivot),这里我们常用的就是那我们的最左边的数当作基准。
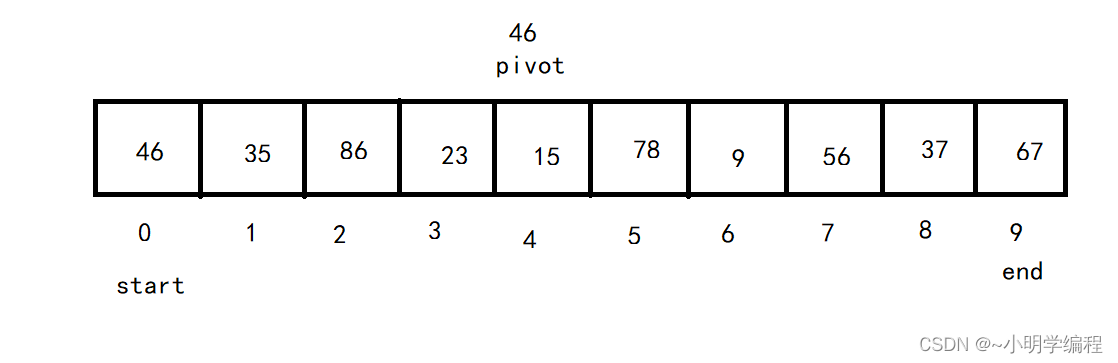
2.我们从左向右找一个比pivot大的数,然后再从右向左找一个比pivot小的数,
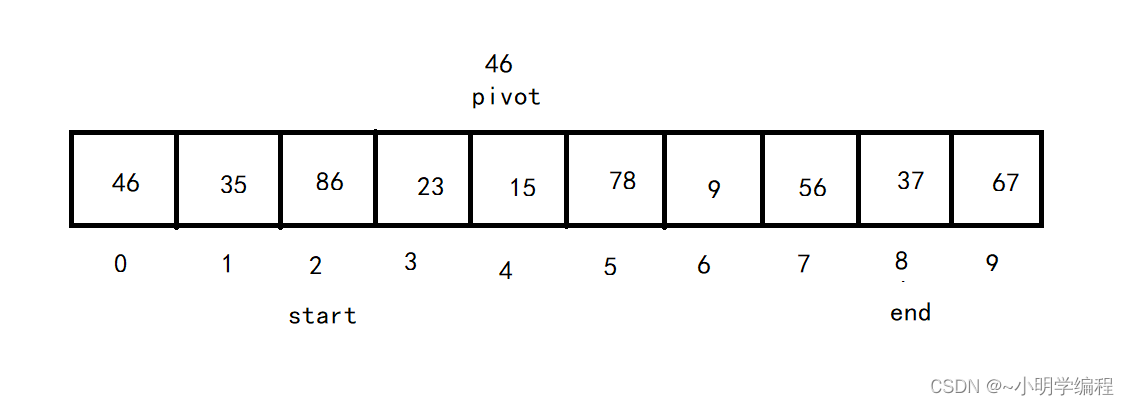
接着交换这两个数,
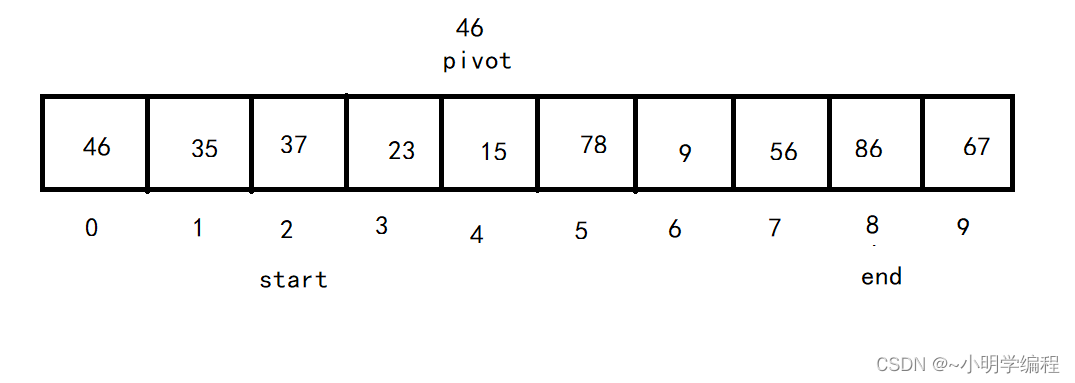
然后重复这个过程直至start==end,
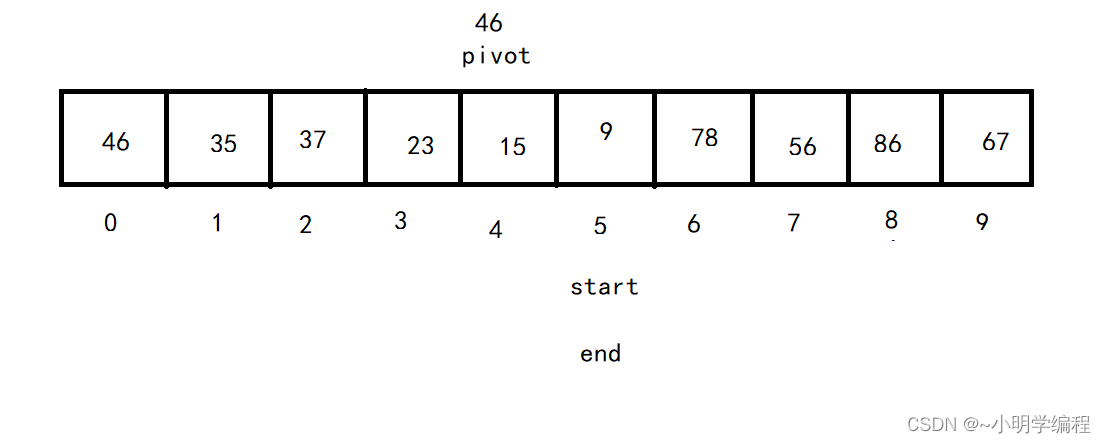
然后就是交换pivot位置的值和start位置的值,
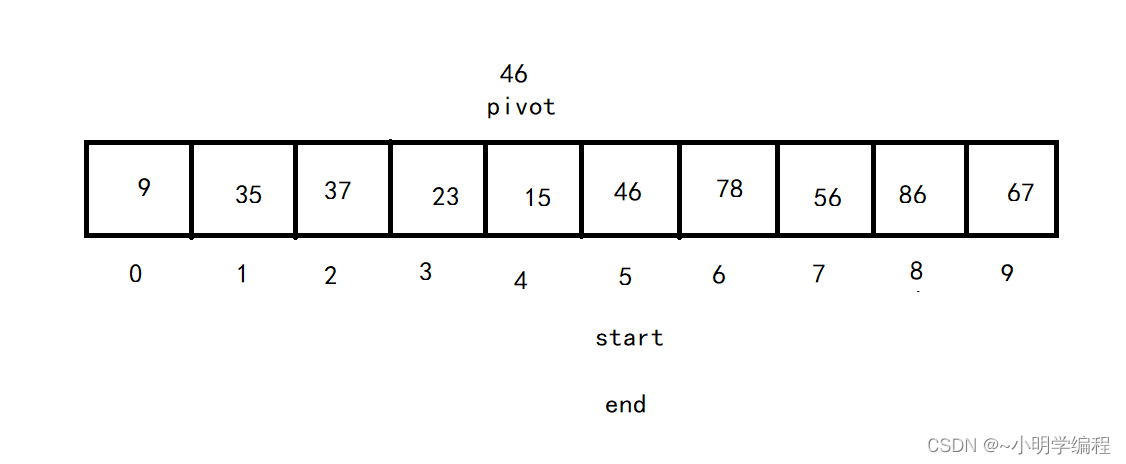
至此,pivot左边的值都小于pivot,右边的值都大于pivot。
3.采用分治思想,对基准的左右两个小区间按照同样的方式处理,直到start>end。
优化
先看一段代码
public static void test1(int capacity) {
int[] array = new int[capacity];
Random random = new Random();
for (int i = 0; i < capacity; i++) {
array[i] = i;
}
long start = System.currentTimeMillis();
quickSort(array);
long end = System.currentTimeMillis();
System.out.println(end-start);
}
public static void main(String[] args) {
test1(100000);
}这里我们给了十万个有序的数据进行排序,看看能不能完成我们的排序。
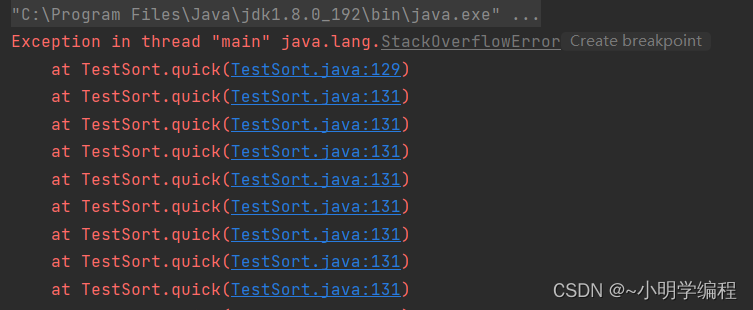
当我们运行代码的时候会发现报错,说我们的栈溢出了。因为当我们的数据比较有序的时候就相当于一个单一的链表。然后就一直开辟栈的空间直到我们的栈溢出。
想要避免这种情况的发生就必须让我们的快速排序尽量的从中间分开形成尽可能的完全二叉树。这样可以大大降低我们的栈的开辟。
在待排序区间选择一个基准值
1. 选择左边或者右边
2. 随机选取
3. 几数取中法
常见的选基准法有这三种其中的第一种也是我们前面用的那种,这种方法有较大的缺陷当我们的待排序列非常有序或者倒序的时候会非常的慢,然后就是随机选取法这种方法比较看脸因人而异也不是很建议,最后就是我们的几数随机取中法,下面给大家介绍。
我们现在就需要写一个方法找出一个尽量中间的数来作为我们的基准。
思路:
我们每次进行递归的时候会传入我们最左边和最右边两个数,然后我们取这两个数的中间下标,然后比较这三个数的大小,找到中间值,然后返回其下标,最后将当前的下标和我们的left的下标做交换。
代码
public static void quick(int[] array,int left,int right) {
if (left>right) {
return;
}
int midIndex = findMidIndex(array,left,right);
swap(array,left,midIndex);
int pivot = partition(array,left,right);
quick(array,left,pivot-1);
quick(array,pivot+1,right);
}
public static int findMidIndex(int[] array,int start,int end) {
int minIndex = start+(end-start)/2;
if (array[start]<array[end]) {
if (array[minIndex]<array[start]) {
return start;
} else if (array[minIndex]<array[end]) {
return minIndex;
} else {
return end;
}
} else {
if (array[minIndex]<array[end]) {
return end;
} else if (array[minIndex]<array[start]) {
return minIndex;
} else {
return start;
}
}
} 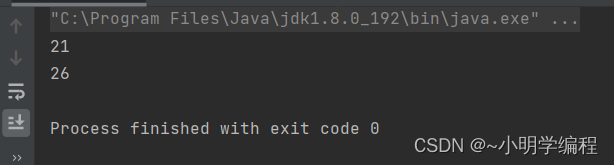
可以看到即使我们的数据上升到了十万级这个量级仍然二十几毫秒就排好序了,反而数据越有序排的越快,将我们的缺点变成了优点。
设置阈值
我们知道当我们的快速排序进行到后期的时候我们的待排序列已经基本上趋于有序了,我们还知道我们的插入排序是越有序,排的就越快,所以现在我们有一个想法,那就是设置一个阈值,当我们快速排序的待排序列低于这个阈值的时候,我们就采用我们的插入排序,这样也能进一步的减少时间。
代码
public static void quick(int[] array,int left,int right) {
if (left>right) {
return;
}
//当我们的待排序个数小于1000的时候我们改为使用插入排序
if (left+right+1<1000) {
insertSort2(array, left, right);
}
//找到我们的中间基准
int midIndex = findMidIndex(array,left,right);
swap(array,left,midIndex);
int pivot = partition(array,left,right);
quick(array,left,pivot-1);
quick(array,pivot+1,right);
}
//针对快速排序而制定的插入排序
public static void insertSort2(int[] array,int left,int right) {
for (int i = left+1; i <= right ; i++) {
int temp = array[i];
int j = i-1;
for (; j >= left ; j--) {
if (array[j] > temp) {
array[j+1] = array[j];
} else {
break;
}
}
array[j+1] = temp;
}
}非递归法
其思想是先将我们的right和left放入栈中,
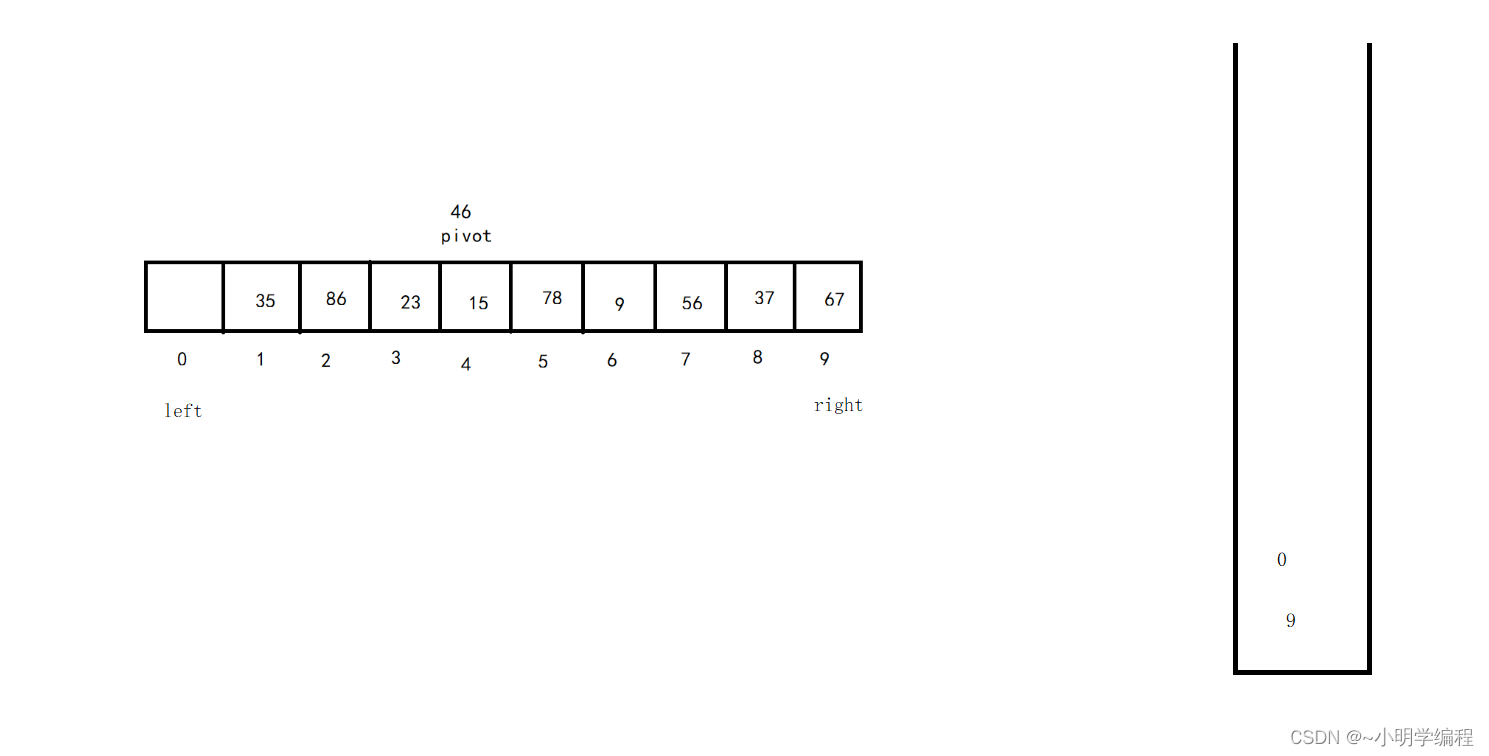
接着出栈,分别将left和right赋值,然后进行排序返回我们的基准值的下标,然后分别将right和pivot+1还有pivot-1和left给压栈,接着重复当前的过程知道栈为空或者left>=right,当然在这期间也可以加入我们的优化。
代码
//快速排序非递归
public static void quickSort1(int[] array) {
Stack<Integer> stack = new Stack<>();
int left = 0;
int right = array.length-1;
//先将最右和最左放入栈中
stack.push(right);
stack.push(left);
while (!stack.empty()) {
//弹出我们的左右两个位置的下标
left = stack.pop();
right = stack.pop();
//当我们的左下标大于等于右下标的时候则跳过当前的排序
if (left>=right) {
continue;
}
int midIndex = findMidIndex(array,left,right);
swap(array,left,midIndex);
int pivot = partition(array,left,right);
stack.push(right);
stack.push(pivot+1);
stack.push(pivot-1);
stack.push(left);
}
}性能

归并排序
原理
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
简单的来说就是将我们待排序的序列一次分成两份,然后将两份再分成四份···,最后分成一份只有一个元素,然后再合并合并的时候因为要合并的两个已经是有序了,所以就转换成合并两个有序数组的问题了。
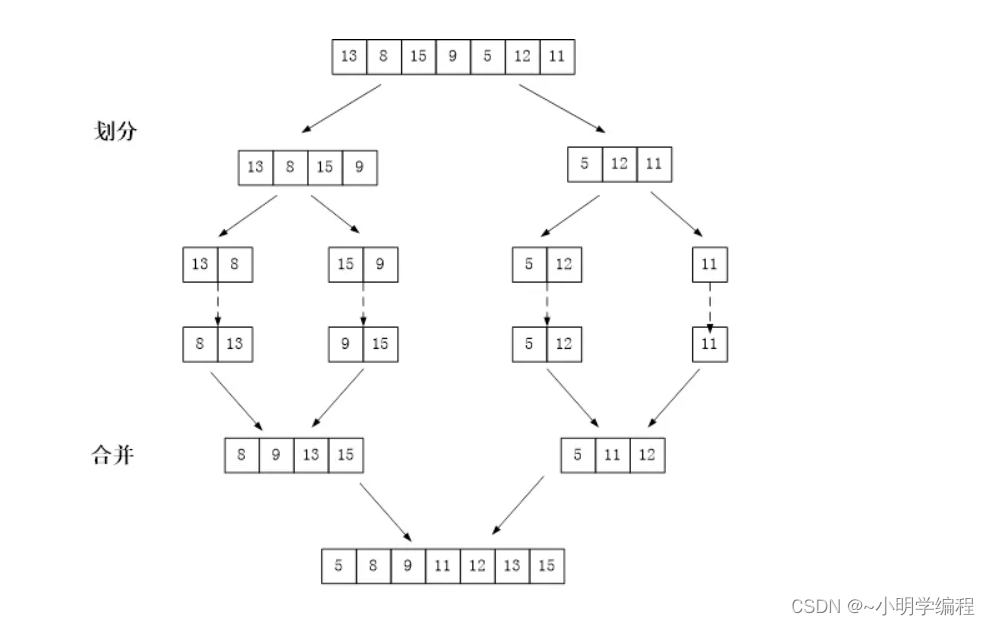
代码
递归法
递归法写起来比较容易理解,就是将我们原数组分成两部分,我们取一个中间值,先递归左边的部分再递归右边的部分,最后写好我们的额合并方法就行了。
//归并排序(递归)
public static void mergeSort(int[] array) {
mergeSortInternal(array,0, array.length-1);
}
private static void mergeSortInternal(int[] array,int low,int high) {
if (low>=high) {
return;
}
int mid = low + (high-low) / 2;
mergeSortInternal(array,low,mid);
mergeSortInternal(array,mid+1,high);
//合并
merge(array,low,mid,high);
}
//合并两个有序的数组
private static void merge(int[] array,int low,int mid,int high) {
int newLength = high - low + 1;
int[] newArray = new int[newLength];
int newArrayIndex = 0;//新数组的下标
int start1 = low;//数组1的开始
int end1 = mid;//数组1的结尾
int start2 = mid+1;//数组2的开始
int end2 = high;//数组2的结尾
//循环直到其中一个数组遍历完
while (start1<=end1 && start2<=end2) {
if (array[start1]<array[start2]) {
newArray[newArrayIndex++] = array[start1++];
} else {
newArray[newArrayIndex++] = array[start2++];
}
}
//将没遍历完的数组剩余的元素给到新数组中
while (start2<=end2) {
newArray[newArrayIndex++] = array[start2++];
}
while (start1<=end1) {
newArray[newArrayIndex++] = array[start1++];
}
//拷贝当前数组到原数组中
for (int i = 0; i < newLength; i++) {
array[i+low] = newArray[i];
}
}非递归法
非递归法写起来就相对的繁琐一点,但是代码却不繁琐,想明白了就很简单。
首先我们定义一个gap表示我们每组的元素个数,我们的i表示我们两个组的首位置,因为我们要合并两个组的数据(当合并只有一组的时候我们merge会直接return)。
left = i,mid = i + gap - 1,right = mid + gap。
//归并排序(非递归)
public static void mergeSort1(int[] array) {
int gap = 1;//每组的元素个数
while (gap< array.length) {
for (int i = 0; i < array.length; i += gap*2) {
int left = i;
int mid = i + gap - 1;
if (mid >= array.length) {
mid = array.length-1;
}
int right = mid + gap;
if (right >= array.length) {
right = array.length-1;
}
merge(array,left,mid,right);
}
gap *= 2;
}
}性能
| 时间复杂度 | 空间复杂度 |
| O(n * log(n)) | O(n) |
| 数据不敏感 | 数据不敏感 |
总结对比
| 排序方法 | 最好 | 平均 | 最坏 | 空间复杂度 | 稳定性 |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | O(n) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(1) | 不稳定 |
| 快速排序 | O(n * log(n)) | O(n * log(n)) | O(n^2) | O(log(n)) ~ O(n) | 不稳定 |
| 归并排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(n) | 稳定 |