有两个题
- 1.第一题
- 2.第二题
1.第一题
😋题目描述：
给定一个整数数组A=(ao，a1，…,an-1),若岗且ai>aj，则<ai.aj>就为一个逆序对。例如数组（3,1,4,5,2,）的逆序对有<3,1>、< 3,2>、<4,2>、<5,2>。编写一个实验程序采用分治法求A中逆序对的个数,即逆序数。
思路：
- 暴力法
从第一个数开始枚举，找到后面所有小于当前的数。
比如：数组是a[5]=3 1 2 5 4
第一步：找到比3大的所有数（但必须在3后面找）
（3，5） ，（3，4）
第二步：找到比1大的所有数（必须在1后面找）
没有
第三步：找到比2大的所有数
没有
第四步：找到所有比5大的数
（5，4）
综上：该数组的所有逆序对就是：(3,5)(3,4)(5,4)
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1010;
int w[N]; // 存储数组
int n;
int main()
{
cout << "输入数组长度：";
cin >> n;
cout << "输入数组元素：";
for (int i = 1; i <= n; i++) //记录数字
cin >> w[i];
int res = 0;
for (int i = 1; i < n; i++) //枚举逆序对的第一个数
for (int j = i + 1; j <= n;j++) //枚举逆序对的第二个数
{
if (w[i] > w[j])
{
cout << "(" << w[i] << "," << w[j] << ") ";
res++;
}
}
cout << endl<< res;
return 0;
}
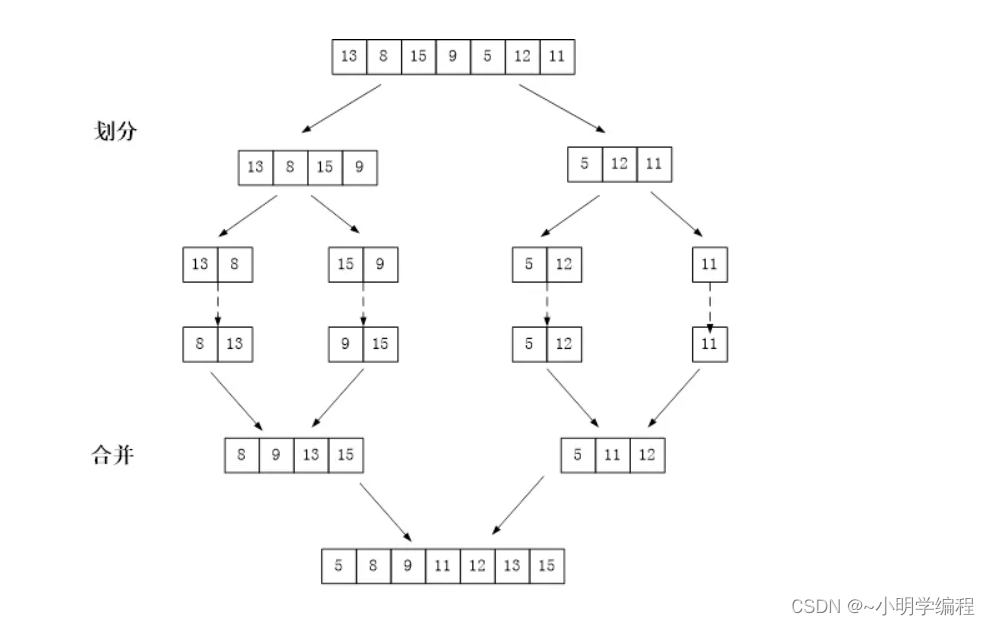
2.分治法
分治法的思想：分而治之，将一个大问题分解成若干个小问题。通过解决小问题，从而解决大问题。关于大问题和小问题的关系，有下面几点
- 大问题的性质和小问题的性质应该是一样的
- 小问题的解决方法和小问题的解决方法也是相同的
对于这道题，分析是这样的：
这道题目使用暴力做法的根本原因就在于数组是“无序”的。
如果将数组一分为二，分成两个小数组，两个小数组都是有序的（从小到大）。那么问题就很简单了。具体看下面的模拟：
假设一个数组：8 9 11 14 9 10 11 13
由此可以发现，只要每次将两个子数组排好序，那么就可以找到两个子数组的所有逆序对。两个子数组合并和成为新的数组（有序）。这样就保证没有遗漏：
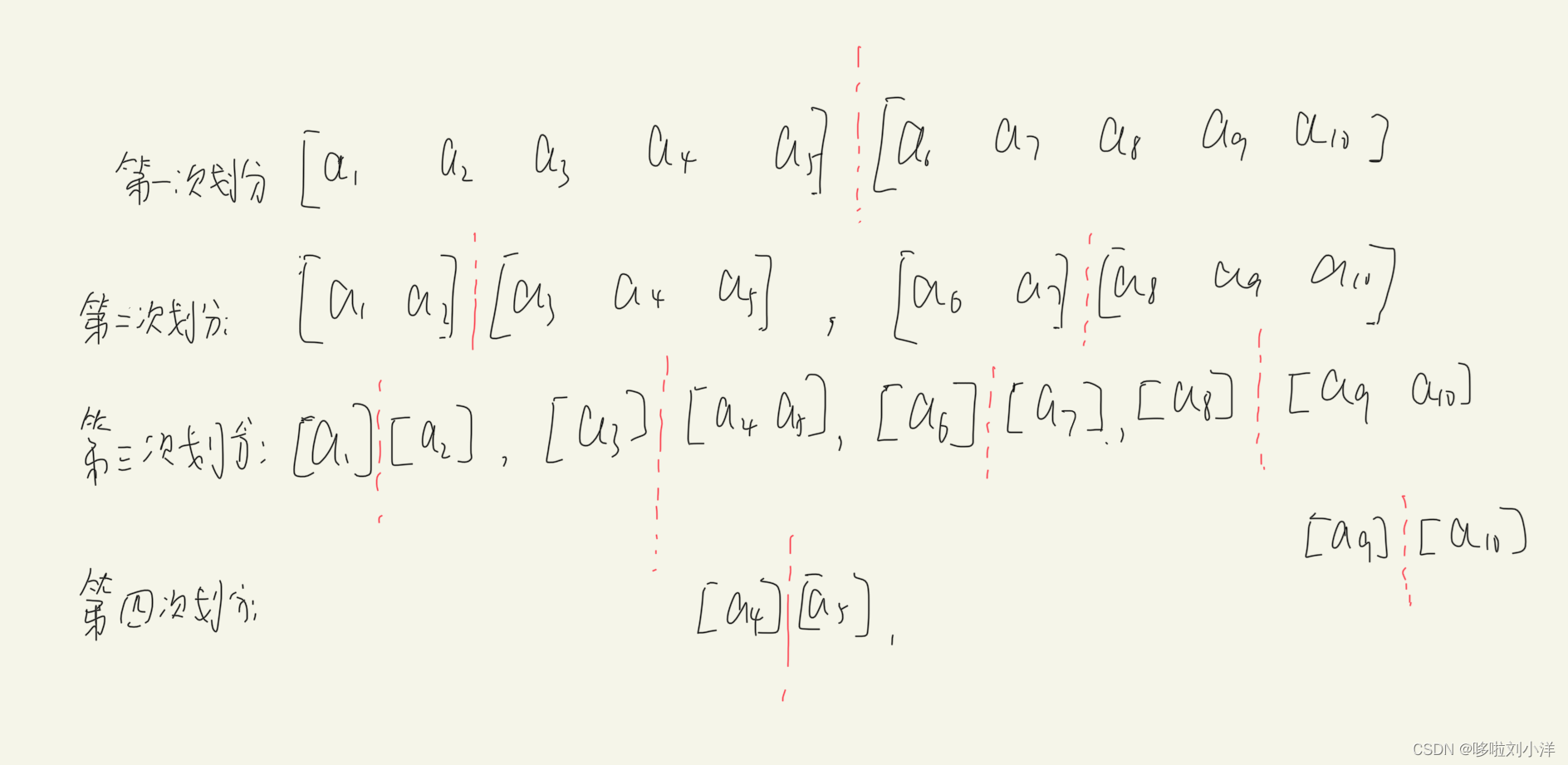数组的逆序对=（左半部分的逆序对+右半部分的逆序对）+左右合并数组的逆序对（左半部分一个数，右半部分一个数组成的逆序对)
先从最后一次划分开始，[a4]和[a5]比较，如果a4>a5，那么逆序对+1，并且将a4,a5从小到大排序。那么子数组[a4 a5]排序完成且找到该区间的所有逆序对。此时可以发现[a3],[a4 a5]都是有序的，那么继续找逆序对且将两个区间进行排序。得到[a3 a4 a5]数组是有序的且该数组的所有逆序对都找到。以此类推。。。讲的不是很清楚，看代码更容易懂（个人感觉）
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
int w[N]; //存储数组
int n;
int merge(int left,int mid,int right) //合并
{
int temp[1010];//临时数组
memset(temp, 0, sizeof(temp)); //数组初始化0
for (int i = left; i <= right; i++)
temp[i] = w[i];
//下面的步骤是归并排序的核心
//将两个有序的区间合并为一个，边合并的同时边累加逆序数对
int sum = 0;
int i = left, j = mid + 1;
int k = left;
while(i<=mid&&j<=right) //哪个小哪个放进数组，然后指针后移。
{
if (temp[i] > temp[j])//枚举后半部分，如果左边当前的值大于右边的值，那么从左边当前的值到后面的所有值多可以组成逆序对
{
sum += mid - i + 1;
w[k++] = temp[j];
j++;
}
else
{
w[k++] = temp[i];
i++;
}
}
while (i <= mid) //左半部分还有值没有放进数组
w[k++] = temp[i++];
while (j <= right) //右半部分还有值没有放进数组
w[k++] = temp[j++];
return sum;
}
int divide(int left,int right) //divide的中文意思是分开.为什么是int，我们想要记录多少逆序数对，那么每次返回的值都是逆序数对个数
{
//将区间分为两个部分，不停二分，最后合并
//凡是递归，先考虑边界,考虑边界的意义是什么
if (left >= right) //当区间只有一个值，就不能分了，不和规定。因为我们是需要不同的二分区间，一个单位长度无法二分。
return 0;
int mid = (left + right) >> 1; //等价(left+right)/2
int a=divide(left, mid); //左边的逆序数对
int b=divide(mid + 1, right); //右边的逆序数对
int c = merge(left, mid, right); //整个区间的逆序数对（感觉有点像区间dp的思维）
return a + b + c;
}
int main()
{
cout << "输入数组长度：";
cin >> n;
cout << "输入数组：";
for (int i = 1; i <= n; i++)
cin >> w[i];
//先分再合。从最底层合的时候就开始排序。这样就保证每一次合并数组都是有序的。
int res = 0;
res = divide(1, n);
for (int i = 1; i <= n; i++)
cout << w[i] << " ";
cout << endl;
cout << "数组的逆序对数量是:" << res << endl;
return 0;
}
2.第二题
😋题目描述：
已知由n(n≥2)个正整数构成的集合A={ak}（0=<k<n),将其划分为两个不相交的子集A1和A2，元素个数分别是n1和n2,A1和A2中的元素之和分别为S1和S2。设计一个尽可能高效的划分算法,满足|n1-n2|最小且|S1-S2|最大,算法返回|S1-S2|
思路：
- 要满足|n1-n2|最小，有两种情况，如果数组长度是偶数，将数组分为等长两半的时候|n1-n2|最小。如果数组长度是奇数，数组分为等长两半，剩余一个元素任意加在一边即可保证|n1-n2|最小。
- 要满足|S1-S2|最大，那么要S1尽可能大，S2尽可能小。这样实际上只需要将数组从小到大排序，右边一半之和为S1，左边一半之和为S2。
排序算法很多种，其中快速排序是效率最高的🐯（反正算法里面只要和排序有关使用快排准没错）
下面的代码里面的快排函数就是百分之百没有错误的快速排序模板，可以直接背诵，效率极高
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
int w[N];
int n;
void fast_sort(int left,int right) //从小到大 快速排序模板，拿去不谢，这个模板过了无数题。
{
int L = left, R = right;
int mid = w[(L + R) / 2];
while (L < R)
{
while (mid > w[L])L++;
while (mid < w[R])R--;
if (L <= R)
{
int temp = w[L];
w[L] = w[R];
w[R] = temp;
L++, R--;
}
}
if (R > left) //R左边的数一定是小于mid
fast_sort(left, R);
if (L < right) //L右边的数一定大于mid
fast_sort(L, right);
}
int main()
{
cout << "输入数组长度:";
cin >> n;
cout << "输入数组：";
for (int i = 1; i <= n; i++) //输入元素
cin >> w[i];
fast_sort(1, n); //快速排序
for (int i = 1; i <= n; i++) //输出一下数组看是否排序成功
cout << w[i] << " ";
cout << endl;
//由于要|n1-n2|最小，那么就二分数组。
int s1, s2;
s1 = s2 = 0;
for (int i = 1; i <= n / 2; i++) //因为n/2是向下取整，所有如果n是奇数，那么右边会多分一个。如果是偶数，两边分的一样多
{
s1 += w[i]; //左边一半的元素之和
}
for (int i = n / 2 + 1; i <= n; i++)
{
s2 += w[i]; //右边一半的元素之和
}
s1 = s1 - s2 > 0 ? s1 - s2 : s2 - s1; //s1-s2可能是负数，要取正数
cout << "|s1-s2|的最大值是:" << s1 << endl;
return 0;
}
新思路！
我们发现：
S1=a1+a2+…an/2
S2=an/2+1+…+an
这代表什么？对于S1,我们实际上不需要一个严格的排过序的数组，而只要满足an/2大于前面所有的数即可。对于S2,不需要排过序的数组，而只要满足an大于前面所有的数即可。
再总结一下，假设有n(假设n是奇数）个数，只要找到一个数target，它满足下面这个性质：
- target左边有n/2个元素且target大于他们
- target右边有n/2个数且target小于他们
说明：这个代码的细节有点难理解，建议使用老师代码，参考上面思路即可
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1010;
int a[N];
int fast_sort(int left, int right)//快速排序模板稍微变形一下
{
int L = left, R = right;
int target = a[(L + R) / 2]; //基准元素是target，下面的目的就是将所有小于等于target的放在它左边，所有大于等于target的放在它右边
while (L < R)
{
while (a[L] < target)L++; //如果左边的元素小于target，说明这个元素是合法的，L往右边移动一个单位
while (a[R] > target)R--; //如果右边的元素大于target，说明这个元素也是合法的，不用移动位置。R往左边移动一个单位
if (L <= R) //3 4 5 7 2 6 9 3 4 5 6 2 7 9
{
int temp = a[L];
a[L] = a[R];
a[R] = temp;
if (L == R) //此时L左边的数都小于等于target,
return L;
L++, R--;
}
}
if (target <= a[L])
return L;
else
return L - 1;
}
void Solve(int n)//目的是找到一个目标值，这个目标值大于等于左边的数，且他们的个数为n/2
{
bool judge = true;
int s1 = 0, s2 = 0;
int left = 1, right = n; //数组左右边界
while (judge)
{
int k = fast_sort(left, right); //k表示左边部分的个数（这左边部分都满足小于等于target)
if (k == n / 2) //满足条件，退出循环
{
judge = false;
}
else if (k > n / 2) //说明target太大，要找一个比target小的数，由于之前排序已经将比target小的数放它左边,所以在左区间找
{
right = k - 1;
}
else
left = k + 1;
}
for (int i = 1; i <= n / 2; i++)
s1 += a[i];
for (int i = n / 2 + 1; i <= n; i++)
s2 += a[i];
cout << "s1-s2=" << s2 - s1 << endl;
}
int main()
{
int n;
cout << "输入元素个数：";
cin >> n;
cout << "输入元素值：";
for (int i = 1; i <= n; i++) //输入元素
cin >> a[i];
Solve(n);
return 0;
}
