文章目录
- 留出法(hold-out)
- Artifact (error)
- 理解交叉熵损失函数(CrossEntropy Loss)
- 信息量
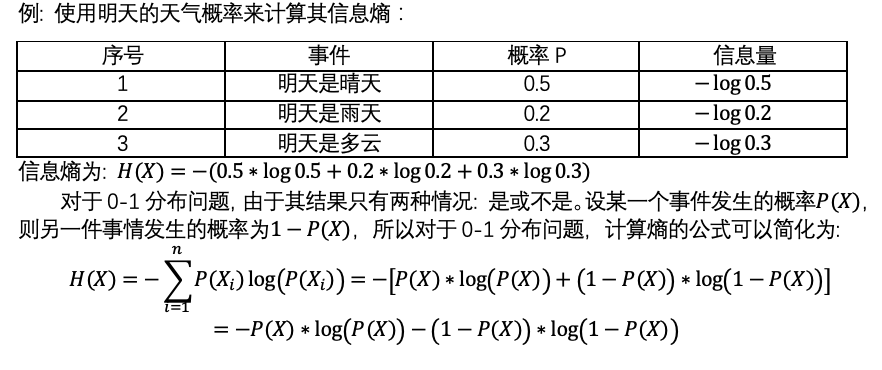
- 信息熵
- 相对熵(KL散度)
- 交叉熵
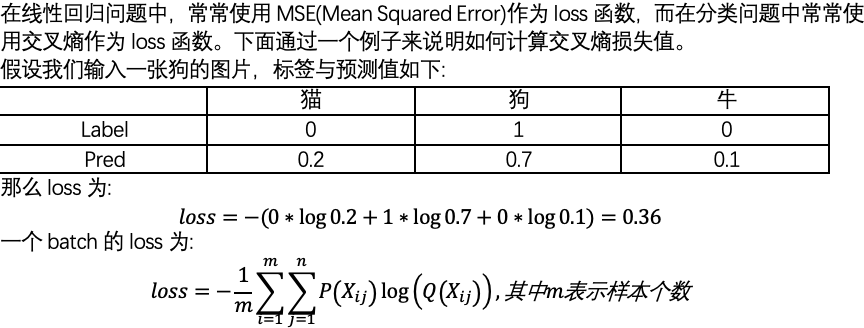
- 交叉熵在单分类问题中的应用
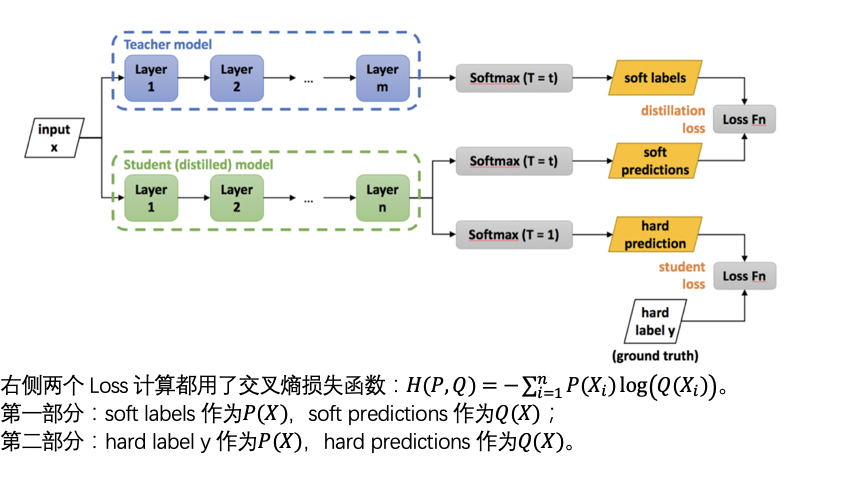
- 回顾知识蒸馏公式
- 对抗学习
- 随机投影(Random Projection)
- 概述
- 基本实现
- sklearn中的随机投影
- 独立成分分析(ICA)
- ICA算法
- ICA 应用
- sklearn 中的ICA
- 项目
留出法(hold-out)
留出法的含义是:直接将数据集D划分为两个互斥的集合,其中一个集合作为训练集S,另外一个作为测试集T,即D=S∪T,S∩T=0。在S上训练出模型后,用T来评估其测试误差,作为对泛化误差的评估。其中T也叫held-out data。
需要注意的问题:
- 训练/测试集的划分要尽可能的保持数据分布的一致性,避免因数据划分过程引入额外的偏差而对最终结果产生影响;
- 在给定训练/测试集的样本比例后,仍然存在多种划分方式对初始数据集D进行划分,可能会对模型评估的结果产生影响。因此,单次使用留出法得到的结果往往不够稳定可靠,在使用留出法时,一般采用若干次随机划分、重复进行实验评估后取得平均值作为留出法的评估结果;
- 此外,我们希望评估的是用D训练出的模型的性能,但是留出法需划分训练/测试集,这就会导致一个窘境:若训练集S包含大多数的样本,则训练出的模型可能更接近于D训练出的模型,但是由于T比较小,评估结果可能不够稳定准确;若测试集T包含多一些样本,则训练集S与D的差别更大,被评估的模型与用D训练出的模型相比可能就会有较大的误差,从而降低了评估结果的保真性(fidelity)。因此,常见的做法是:将大约2/3~4/5的样本用于训练,剩余样本作为测试
来源于周志华的西瓜书。
Artifact (error)
In natural science and signal processing, an artifact is any error in the perception or representation of any information introduced by the involved equipment or technique(s).
在自然科学和信号处理中,“artifact”是指相关设备或技术引入的任何信息的感知或表示中的任何错误。
In computer science, digital artifacts are anomalies introduced into digital signals as a result of digital signal processing.
在计算机科学中,数字伪影是由于数字信号处理而引入数字信号中的异常现象。
理解交叉熵损失函数(CrossEntropy Loss)
深度学习代码中经常看见“交叉熵损失函数”,它是“分类问题”中常用的一种损失函数,而且在使用交叉熵作为损失函数时,模型的输出层总会接一个softmax函数。交叉熵是信息论中的一个重要概念,主要用于度量两个概率分布间的差异性,要理解交叉熵,先解释以下几个名词。
信息量

信息熵

相对熵(KL散度)

交叉熵
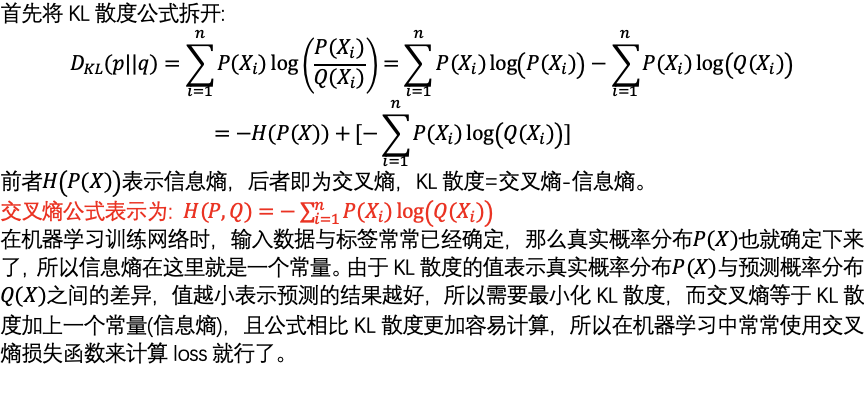
交叉熵在单分类问题中的应用
回顾知识蒸馏公式
对抗学习







5. 对抗学习的科研前沿
目前,对抗攻击中攻击与防御的方式也是“道高一尺,魔高一丈”,已经经过了许多轮的迭代,演变出了许多攻防方式。随着各种攻击方法的产生,提出的防御方法看似抵御了这些攻击,但是新出现的攻击却又不断躲避着这些防御方法。
至今,人们仍不完全清楚神经网络这个黑盒的本质特性。甚至有研究指出,神经网络完成的分类任务仅是靠辨别局部的颜色和纹理信息,这使得自然的对抗样本,即便不是人为加入的扰动,而是真实采集到的图像,也能够成功地欺骗神经网络。
这也支持了许多研究者的观点,即神经网络只是学习了数据,而非知识,机器学习还无法像人一样学习。这项难题的最终解决,或许依赖于对神经网络的透彻理解,以及对神经网络结构的改进。
弄清楚神经网络内部的学习机制,并据此进行改进,或许才能真正解决目前神经网络对于对抗攻击的脆弱性。因此对抗机器学习不仅是机器学习被更加广泛地被应用的一道门槛,也是促使人们研究如何解释机器学习模型的动力。
随机投影(Random Projection)
概述
随机投影是一种比较有效的降维方法,在计算上比主成成分分析更有效。它通常应用于当数据有太多维度,假定运行程序的资源有限,主成成分分析无法有效计算的时候。
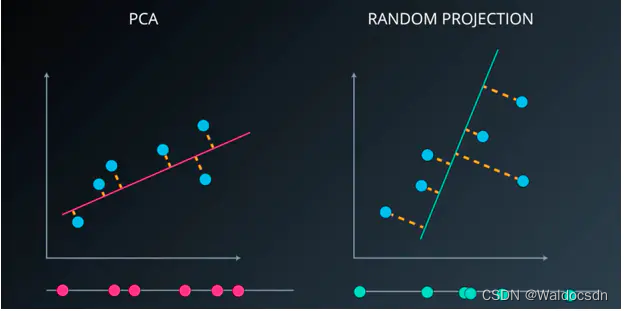
一个简单化的案例,对PCA 和 随机投影。如下图:
PCA:将一个数据集从二维降至一维,PCA的做法是寻找方差最大化的方向,然后将数据投影到最大化方差的方向。该过程将产生最小损伤。
随机投影:在数据有很多维度时,会消耗一定的资源。通常情况下会随机选择一条直线,任何一条进行投影。在某些情景下没有太大的意义,但在更高维度下效果比较好,且效率高。
基本实现
随机投影的基本前提是:用数据集乘以一个随机矩阵来减少其中的维度。在某种程度上讲,这就是随机投影。
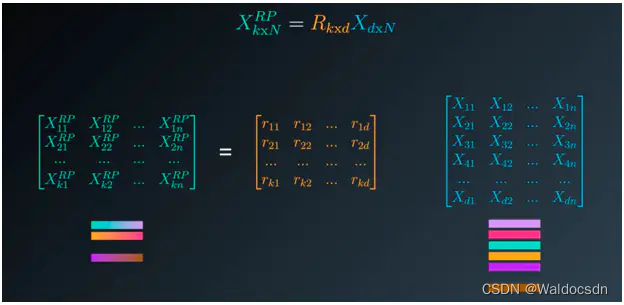
一个简单的案例。如下图:
假如数据集有 12000 列,1500 个样本。这已经可以说是高维度数据集了。将数据集输入到sklearn中随机投影,返回到结果是6268 列、1500 个样本的数据集:
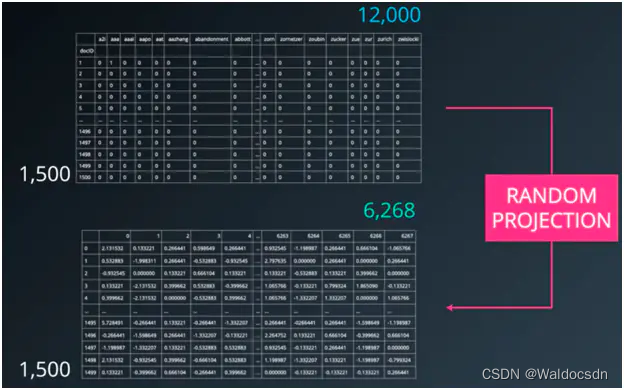
在随机投影中,其实是将原数据集乘以一个随机矩阵就可以被映射成低维的空间。在这种程度下,每两点之间的距离、每对之间的距离在某种程度下得到了保留。这很重要,因为在非监督学习和监督学习中,很多算法都与点之间的距离有关,所以需要保证距离有些失真,但可以保留。
如何保证投影之后的距离得以保留?Johnson-Lindenstrauss引理指出:投影后两点的距离平方值稍有压缩。它大于原数据集两点之间的平方值乘以 (1 - eps) ;小于原数据集两点之间的平方值乘以(1 + eps) 。
如果两点之间距离的平方值为 125.6 。 eps 为 0 ~ 1 之间的值,在sklearn中默认为 0.1。

eps 如同一个操作杆,用于计算产生了多少列,并在此维度是可接受的失真水平。eps 是输入到函数中,用此来在此程度下保证距离。
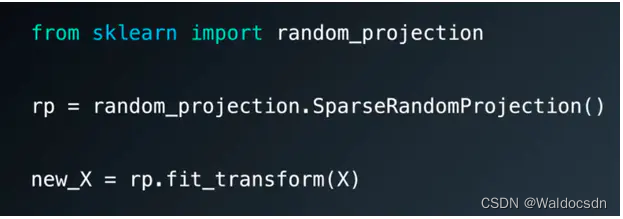
sklearn中的随机投影
sklearn 中随机投影的案例:http://lijiancheng0614.github.io/scikit-learn/auto_examples/plot_johnson_lindenstrauss_bound.html#example-plot-johnson-lindenstrauss-bound-py
sklearn 中随机投影API:http://lijiancheng0614.github.io/scikit-learn/modules/generated/sklearn.random_projection.SparseRandomProjection.html#sklearn.random_projection.SparseRandomProjection
独立成分分析(ICA)
独立成分分析(ICA) 是同主成成分分析(PCA) 和 随机投影相似的方法。同样会通过一些数据集特征产生另一个作用数据集。但不同的是PCA用于最大化方差,ICA 则假设这些特征是独立源的混合。并尝试分离这些独立源。
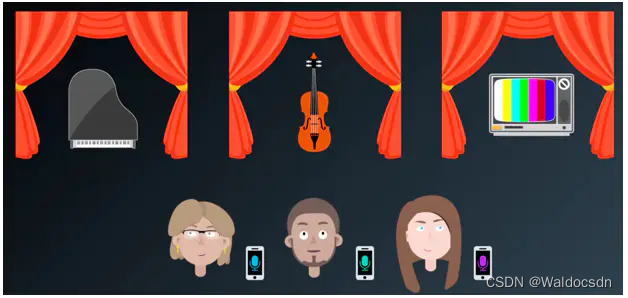
假定有三个朋友参加艺术展览,展览会上同时有着钢琴声、小提琴声、电视声。三个人各在不同声音的旁边,同时用手机录取下来听到的声音。
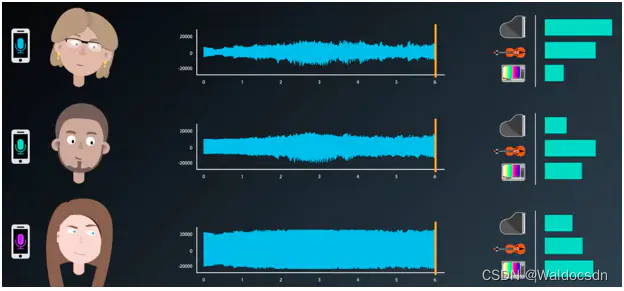
三个朋友录取的声音都有不同的来源,靠近钢琴的朋友,录取到的钢琴声比较明显;而其他声音则比较弱。其他两个也是,一个录取的小提琴声音比较明显,一个录取电视声比较明显。
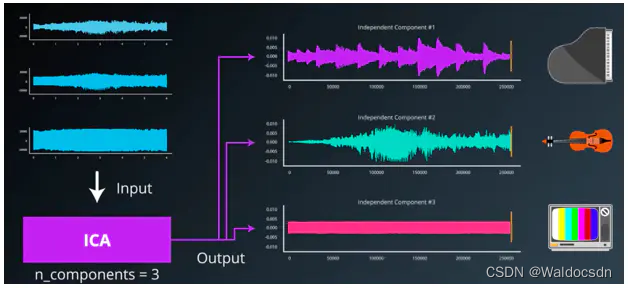
是否可以运用ICA剥离出源声音呢?答案是可以。输入收集的三种数据集,利用ICA算法剥离出源数据。这里的源组成分(这里等于3)
ICA算法
简单介绍 ICA 算法的原理。不会涉及复杂的数学知识。详细的信息可查看论文“独立成分分析:算法与应用”。
现在假设有数据集 X , 假设 X 数据集是由源信号 S 乘以混合矩阵 A 产生的, X = AS。如下图:
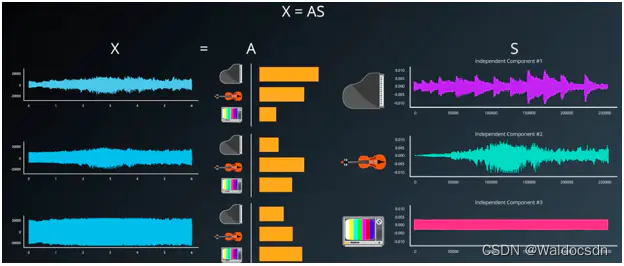
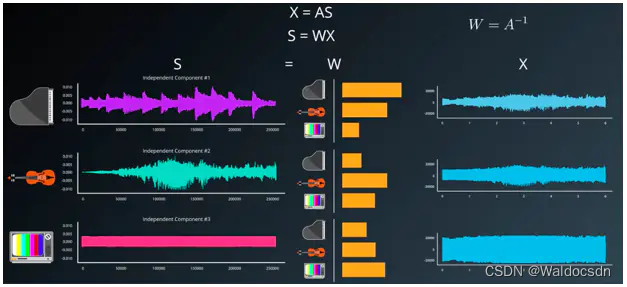
但是现在有数据集 X ,也就是原录音。S 信号源是需要计算得到的结果,A 为混合矩阵。如此需要变换公式,即 S = WX 。 W 为 A 的倒数,如果A是混合矩阵,W 即为非混合矩阵。
在 S = WX 公式中, X 为输入的源数据集。需要得到想要的 S 结果,就需要计算 W ,所以独立分析算法和其过程全部目标是趋近 W ,或者给出最佳的 W 与 X 相乘来产生原始信号。论文“独立成分分析:算法与应用”对算法做出了清楚的解释。
ICA 应用
ICA 被广泛应用于医学扫描仪。一个叫做 EEG或MEG的脑部扫描仪的例子。论文:Independent Component Analysis of Electroencephalographic Data
将 ICA 应用于金融中的因子模型。论文:Applying Independent Component Analysis to Factor Model in Finance
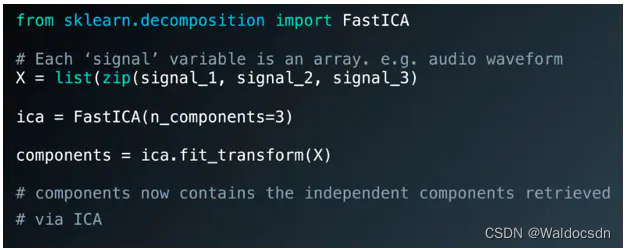
sklearn 中的ICA
sklearn 中 ICA 的API:http://lijiancheng0614.github.io/scikit-learn/modules/generated/sklearn.decomposition.FastICA.html
项目
使用 ICA 提取混合的音频信号。与上述例子一样。在此下载 文件,使用 jupyter notebook 打开查看。
链接: https://pan.baidu.com/s/10SkvkM9dJPMJSzTRIpiPuQ?pwd=6wnn 提取码: 6wnn








![[计算机毕业设计]聚类分析算法](https://img-blog.csdnimg.cn/632f16aceeee4be6a8443d20fb0be8d8.png)