前言
📅大四是整个大学期间最忙碌的时光,一边要忙着准备考研,考公,考教资或者实习为毕业后面临的就业升学做准备,一边要为毕业设计耗费大量精力。近几年各个学校要求的毕设项目越来越难,有不少课题是研究生级别难度的,对本科同学来说是充满挑战。为帮助大家顺利通过和节省时间与精力投入到更重要的就业和考试中去,学长分享优质的选题经验和毕设项目与技术思路。
🚀对毕设有任何疑问都可以问学长哦!
本次分享的课题是
🎯聚类分析算法
课题背景与意义
在现今这个“大数据”流行的时代,机器学习成为了数据挖掘中不可或缺的一部分,而聚类分析是其中最重要的研究分支之一。我国有句俗话,‘物以类聚,人以群分’。
聚类分析(Cluster Analysis),顾名思义是一种将数据集中的样本,根据内在的性质和规律,划分为若干不相交子集的数据归约技术。每个子集称为一个簇(Cluster)或类,是若干个观测值组成的群组,群组内观测值的相似度高于群组间。聚类过程仅仅能自动形成簇,但是簇的概念需要使用者进一步定义或者命名【1,2】。
聚类分析的应用非常广泛,它既可以作为一个单独的工具以发现数据样本中一些隐含的、深层的信息,也可以作为其他数据挖掘分析方法的一个预处理步骤。例如: 一家电商平台需要根据人口学特征和购买习惯等将客户分成不同的小组,比如“年轻白领”、“家庭主妇”、“在校学生”等等类型,以便通过相关的产品接触到他们的目标客户。
课题实现技术思路
聚类不存在客观标准,相对于其他机器学习分支来说,聚类的知识还不够系统化,给定数据集,总能找到以往算法未覆盖的某种标准而设计出新算法,而且不同的书籍讲解聚类的时候,会有不同的分类机构,再加之聚类的新算法层出不穷,因此常常以列举经典算法的形式进行说明讲解。
“西瓜书”列举介绍了如下三大类聚类算法(原型聚类、密度聚类、层次聚类),我们以此为框架,结合其他有关聚类的内容,对其进行讲述:
1、原型聚类
原型聚类假设聚类结构能通过一组原型刻画,通常算法先对原型进行初始化,然后对原型进行迭代更新求解,采用不同的原型表示,将产生不同的算法。实现假定了聚类中心数量时也被称为划分聚类。下面是几种著名的原型聚类算法【1】。
①K均值算法(K-means)
②学习向量量化(LVQ,Learning Vector Quantization)
③高斯混合聚类(Mixture of Gaussian)
④K中心点算法(PAM算法,Partitioning Around Medoids)
2、密度聚类(Density-based clustering)
密度聚类假设聚类结构能通过样本分布的紧密程度确定。通常情形下,密度聚类算法使用一定邻域内点的数量来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。最著名的当属DBSCAN算法。
3、层次聚类(Hierarchical clustering,或称系统聚类)
层次聚类通过计算不同类别的相似度类创建一个有层次的嵌套的树。通俗点说,可以将相似度高的簇进行合并,也可以将相似度低的簇进行分裂,不断重复到预期簇。而衡量相似度最常用的指标是距离。AGNES算法是一种经典的层次聚类方法。
小注:
在学习聚类的时候,很容易就看到其他的分类方法,比如根据聚类对象的不同将划分为R型聚类(对变量进行聚类)或者Q型聚类(对样品进行聚类)。其实都是可以的,聚类分析非常的灵活,我们要根据自己的需要进行聚类,不必拘泥于某种算法归类于某个分类,多看几个实例,进行实战操作,再回头看算法,会对他们的分类有更深的理解。
①K-means
提到聚类就不得不说起K-means,这是一种很典型的基于距离来判断数据相似性的动态聚类算法,就是说我们先初步选定聚类中心,然后挨个计算各个数据到聚类中心的距离,如果误差平方和最小,那么可以认为算法收敛,计算结束。
Step1:任选K个聚类中心,这里蕴含另一个意思,就是你开始就得确定好聚类中心的数量,这可难了,k值的选定非常难以估计,如果选择不合理,可能无法获得有效聚类结果。可能需要结合专业判断外加多次尝试。假设我们选定两个聚类中心。
Step2:分别计算样本数据集中每一个数据与各个聚类中心的距离,并按照最小距离原则,分配给2个聚类中心。举个栗子,其中有一个a点,a点距离聚类中心1距离为3,距离聚类中心2距离为4,则分配a点给聚类中心1。Ps:距离有绝对值距离,明氏距离等,根据需要选用。
Step3:更新聚类中心,根据新分成的2类建立新的聚类中心。
Step4:判断新旧聚类中心是否相等。
Step5:如果不相等,则重新计算各个数据到step3建立的聚类中心的距离,按照最小距离原则,重新分配数据到2个聚类中心。
Step6:更新聚类中心,根据新分成的2类建立新的聚类中心。
Step7:判断新旧聚类中心是否相等,如果相等,此时算法收敛,计算结束。如果不相等,则转到step2。
②LVQ
与k-means算法类似,学习向量量化(LVQ),也是试图找到一组原型向量来刻画聚类结构。但是与K-means不同,LVQ假设数据样本带有类别标记(比如,A部分数据为患病,剩下的B部分数据为非患病,每个数据都有自己的特征:某因素暴露程度评分等等),学习过程利用样本的这些类别标记(相当于监督信息),来辅助聚类。
给定含有m个数据的样本数据集D={(x1,y1),(x2,y2),(x3,y3)...(xm,ym)},每个样本的xj是由n个属性描述的特征向量(xj1,xj2,xj3...xjn),yj∈Y是样本xj的类别标记。LVQ的目标是通过学习迭代,获得一组n维原型向量{p1,p2,p3,p4,...,pq},每个原型向量代表一个聚类簇,簇标记∈Y【1】。
有点拗口,举个例子(自己编造,仅供理解模型。原始数据形式,没做三线表):
| NO | 特征1(xj1):BMI | 特征2(xj2):年龄 | 类别(yj):高血压与否 |
| 1 | 22 | 23 | 2 |
| 2 | 24 | 24 | 2 |
| 3 | 35 | 55 | 1 |
| 4 | 34 | 49 | 1 |
| 5 | 28 | 45 | 1 |
| 6 | 27 | 32 | 2 |
该例子给定含有6个数据的样本数据集D={(x1,y1),(x2,y2),(x3,y3)...(x6,y6)},每个样本的xj是由2个属性描述的特征向量(xj1,xj2),yj∈Y是样本xj的类别标记。LVQ的目标是通过学习迭代,获得一组2维原型向量{p1,p2,p3},每个原型向量代表一个聚类簇,簇标记∈Y。
说人话:我们有这么个6个样本量的数据集,每个数据有2个特征(BMI,年龄),分别归属两类(高血压,非高血压)目标是获得一组2维(BMI,年龄)原型向量{p1,p2,p3}。假定原型向量初始化为NO.1,NO.3,NO.5。
Step1:算法开始时,根据样本的类别标记和簇的预设类别对原型向量进行随机初始化,假定原型向量初始化为NO.1,NO.3,NO.5。
Step2:开始进行第一轮迭代,假设随机选取的样本是NO.2
Step3:计算该样本与当前三个原型向量的距离,找到与该样本距离最近的原型向量(假设是p3)
Step4:判断该样本与当前原型向量所属类别是否一致
Step5:若一致,则更新原型向量:p新=p3+ŋ*(NO.2-P3),P新向NO.2方向靠近
Step6:否则,P新远离NO.2方向p新=p3-ŋ*(NO.2-P3)。Ŋ为学习率,ŋ∈(0,1)
Step7:如果已经达到设定的最大迭代次数,或者原型向量更新很小或者不更新,则算法收敛,将当前原型向量作为结果返回。可以用相应的作图函数,对结果进行可视化。
③Mixture of Gaussian
高斯混合聚类与K-means和LVQ不同,虽都属于原型聚类,但K-means和LVQ以原型向量刻画原型,而高斯混合聚类采用概率模型来表达聚类原型【1】。小伙伴们,看到概率模型四个字,你们和我一样兴奋了吗?在说高斯混合聚类之前,我们必须得搞清楚什么是高斯分布,再搞清楚什么是高斯混合分布。
高斯分布:其实就是正态分布(手动滑稽),因为高斯在正态分布上做了重要的贡献,所以又叫高斯分布,或者叫一元高斯分布。
高斯混合分布【1】:先说一下多元高斯分布,对n维样本空间X中的随机向量x,若x服从高斯分布,其概率密度函数如下:
μ:n维均值向量
∑:n×n协方差矩阵
However,不管是一元高斯分布,还是多元高斯分布,都属于单高斯分布,当我们聚类的时候,肯定是想把一堆乱七八糟的数据聚成几类,而不是把一堆数据拟合成一个较为理想的单高斯模型(单个峰,大致对称)。
So,我们就需要建立高斯混合模型,所谓混合,就是多个单高斯模型的混合。然后,我们可定义高斯混合分布:
该分布由k个混合成分(K个单高斯分布)组成,每个混合成分对应一个高斯分布,其中ui和∑i是第i个高斯分布的参数。
αi是相应的混合系数,α∈(0,1),且αi求和为1
Step1:设置高斯混合成分个数,例如k=2,意思是有2个高斯混合成分,可以聚2类
Step2:初始化高斯混合分布的模型参数,α1,μ1,∑1,α2,μ2,∑2
Step3:根据贝叶斯公式,计算各混合成分生成的后验概率,得到新的模型参数
Step4:模型参数更新后,不断重复迭代,计算新的α1,μ1,∑1,α2,μ2,∑2,就会不断获得不同轮数迭代后的聚类结果
Step5:Plot或者类似函数可视化。
PAM是最早提出的k中心点算法之一,该算法用数据点替换的方法获得最优聚类中心,该算法相对于K-means的一个好处就是可以克服K-means容易获得局部最优的缺点。另外由于K-means计算均值来判断聚类中心,学过统计的都知道,均值很容易受到极端值影响,所以某一或某些极端值就有可能影响算法对于聚类中心的判断。
Step1:随机选择k个对象,作为初始的中心点,每个中心点代表一个簇;
Step2:计算每个样本到中心点的距离(比如,曼哈顿距离),指派每个剩余对象给离该剩余对象最近的簇,总代价为数据点与集群中心的距离之和;
Step3:随机地选择一个未选择过的非中心点对象y;
Step4:计算用y代替中心点的交换代价s=当前总代价-原总代价;
Step5:如果s为负,说明当前总距离比原总距离更小,则可以用y代替x,形成新的中心点;
Step6:重复2-直到k个中心点不再发生变化。
🚀海浪学长的作品示例:
大数据算法项目
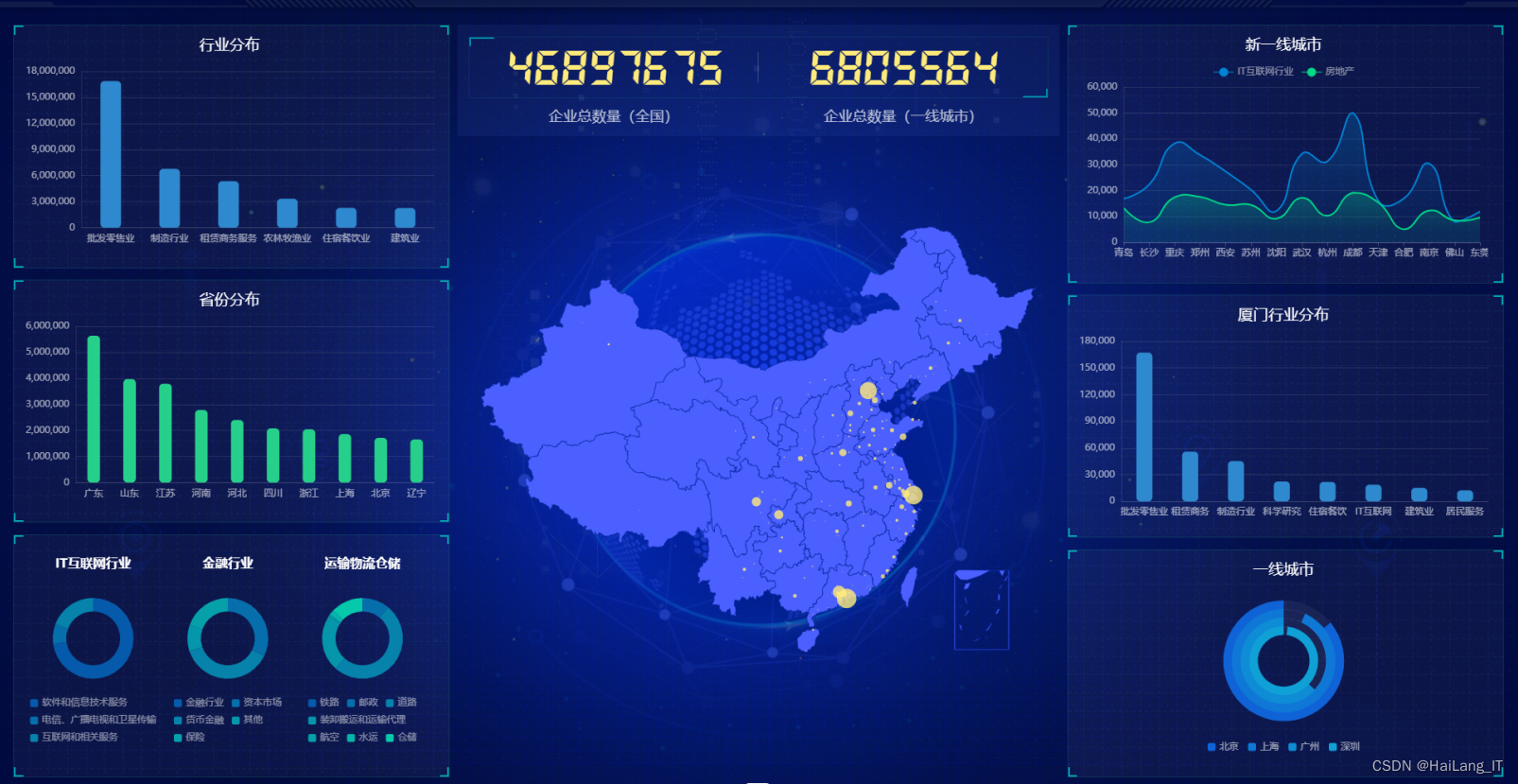
机器视觉算法项目


微信小程序项目
Unity3D游戏项目

最后💯
🏆为帮助大家节省时间,如果对开题选题,或者相关的技术有不理解,不知道毕设如何下手,都可以随时来问学长,我将根据你的具体情况,提供帮助。





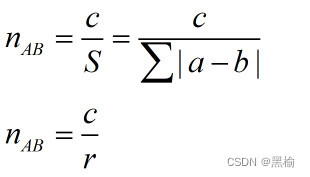



![[附源码]java毕业设计社区空巢老人关爱服务平台](https://img-blog.csdnimg.cn/913996e7bf4c457690aa092fb7a15065.png)
