LeetCode - 300 最长递增子序列

题目来源

题目描述

示例

提示

题目解析

算法源码

题目来源

300. 最长递增子序列 - 力扣（LeetCode）

题目描述

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例

输入	nums = [10,9,2,5,3,7,101,18]
输出	4
说明	最长递增子序列是 [2,3,7,101]，因此长度为 4 。

输入	nums = [0,1,0,3,2,3]
输出	4
说明	无

输入	nums = [7,7,7,7,7,7,7]
输出	1
说明	无

提示

1 <= nums.length <= 2500
-104 <= nums[i] <= 104

题目解析

首先本题描述中说明了递增子序列是可以不连续的，因此本题无法使用双指针来处理。双指针一般只可以求解连续递增子序列。

本题需要使用动态规划的思维，将大问题划分为相同子问题，从子问题中寻找规律。

比如我们需要求下面nums的最长递增子序列，

nums = [10,9,2,5,3,7,101,18]

首先缩小数据规模，先求

nums = [10] 的最长递增子序列，发现就是10

接着扩大数据规模，求

nums = [10,9 ] 的最长递增子序列，新加入元素9，则9尝试和10组合，发现不是严格递增，因此无法组合，因此该子问题得最长递增子序列是9

继续扩大数据规模，求

nums = [10,9,2] 的最长递增子序列，新加入元素2，分别尝试和9子序列合并，和10子序列组合，发现无法形成严格递增，因此无法组合，最终最长递增子序列是2

继续扩大数据规模，求

nums = [10,9,2,5] 的最长递增子序列，新加入元素5，分别尝试和9子序列，10子序列，2子序列组合，发现可以和2子序列形成严格递增，因此得到最长递增子序列为2 5

继续扩大数据规模，求

nums = [10,9,2,5,3]的最长递增子序列，新加入元素3，分别尝试和9子序列，10子序列，2子序列，2 5子序列组合，发现可以和2子序列形成严格递增，因此得到最长递增子序列为2 3

.....

按此逻辑，直到求解道nums原来得数据规模。

我们定义一个dp数组，dp[i]元素值得含义是：以nums[i]结尾的严格递增子序列最大长度，dp数组初始化时，每个元素的初始值都是1，因为严格递增子序列至少有一个nums[i]元素，即序列长度至少为1。

按照上面子问题分解的逻辑，我们可得：

dp[0] = 1

dp[i] = 下面求解过程的最大值

if(num[i] > nums[i-1])

        dp[i] 可能取值 dp[i-1] + 1，如果 dp[i-1] + 1 > dp[i] 的话

if(num[i] > nums[i-2])

        dp[i] 可能取值 dp[i-2] + 1，如果 dp[i-2] + 1 > dp[i] 的话

.....

if(num[i] > nums[0])

        dp[i] 可能取值 dp[0] + 1，如果 dp[0] + 1 > dp[i] 的话

最终代码实现如下

/**
 * @param {number[]} nums
 * @return {number}
 */
var lengthOfLIS = function(nums) {
    const dp = new Array(nums.length).fill(1)

    for(let i = 1; i < nums.length; i++) {
        for(let j = 0; j < i; j++) {
            if(nums[i] > nums[j]) {
                dp[i] = Math.max(dp[i], dp[j] + 1)
            }
        }
    }

    return Math.max.apply(null, dp)
};

上面动态规划的算法时间复杂度差不多是O(n^2)，因此面对1 <= nums.length <= 2500数据规模，也能有上百万次循环。

那么是否存在优化的可能呢？

我们可以发现nums = [10,9,2]这个子问题的有三个递增子序列，分别是10子序列、9子序列以及2子序列。

那么这三个子序列哪个是最优的呢？

所谓最优，即当我为nums = [10,9,2]追加一个数据，那么上面三个子序列哪个是最有可能和追加的数组合在一起，形成一个长度为2的递增子序列呢？

答案是2子序列，因为2 < 9 < 10，如果追加的数可以和9或10组合形成递增子序列，那么一定可以和2组合形成递增子序列。

因此2子序列是是长度为1的最优子序列。

接下来再追加一个数据3，nums = [10,9,2,5,3]

那么哪个子序列是长度为2的最优子序列呢？

首先长度为2的子序列已经有了一个2 5，当追加一个数据3进来后，发现2 3形成的长度为2子序列的子序列更优。因此此时长度为2的最优子序列是2 3。

nums = [10,9,2,5,3,7,101,18]

按照此逻辑，我们可以求得

长度为1的最优子序列为2
长度为2的最优子序列为2 3
长度为3的最优子序列为2 3 7
长度为4的最优子序列为2 3 7 18

其实最优子序列的特性是由子序列的最后一位绝对的，而前面的数据无关，因此我们可以将上面总结改为

长度为1的最优子序列的尾数为2
长度为2的最优子序列的尾数为3
长度为3的最优子序列的尾数为7
长度为4的最优子序列的尾数为18

我们可以重新定义dp数组，dp[i]的含义就是长度为i+1的最优子序列的尾数值。

因此dp数组的长度即为最长递增子序列的长度。

如果大家对于上面逻辑还是不懂，这里还有一个生动的例子可以帮助理解：

即有一组牌 [10,9,2,5,3,7,101,18] ，可以分为多组，但是每组的下面的牌必须比上面的牌大，因此分牌过程如下

首先，取出第一张牌10，放到一组中

接着取出9，发现比10小，因此可以放在10上，此时第一组最上面牌变为9，

接着取出2，发现比9小，因此可以放在9上，此时第一组最长面牌变为2

接着取出5，发现第一组最长的2<5，因此5需要另起一组

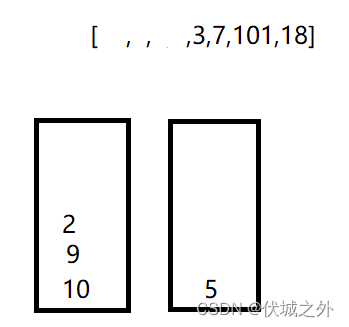
接着取出3，发现比第一组2大，因此尝试放道第二组，发现比5小，因此可以放

同理处理7，101，18

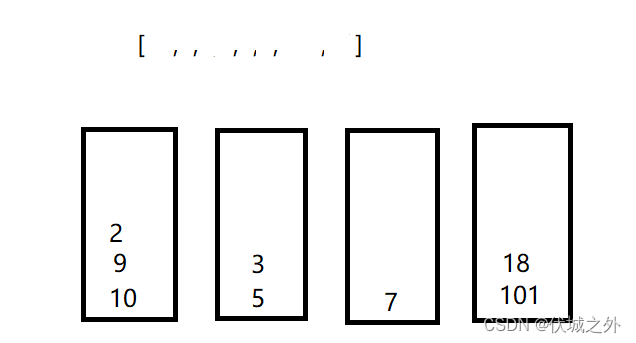
可以发现一共分成了4组，而这就是我们需要求得递增子序列的最长长度。

而这个分牌逻辑其实就是耐心排序，耐心排序同样适用于前面求每个固定长度下，最优子序列的尾数的逻辑，因此算法实现如下

/**
 * @param {number[]} nums
 * @return {number}
 */
var lengthOfLIS = function (nums) {
  const dp = [nums[0]];

  for (let i = 1; i < nums.length; i++) {
    if (nums[i] > dp[dp.length - 1]) {
      dp.push(nums[i]);
      continue;
    }

    for (let j = 0; j < dp.length; j++) {
      if (nums[i] <= dp[j]) {
        dp[j] = nums[i];
        break;
      }
    }
  }

  return dp.length;
};

我们发现，虽然算法的性能得到大幅的提升，但是算法的时间复杂度好像还是O(n^2)。

此时，我们需要注意到上面算法的内层for循环遍历的dp数组其实是一个升序的，如下图所示

而内层for想要完成的功能是，找到第一个比nums[i]大的dp[j]，然后将nums[i]作为dp[j]的新值。

而dp本身是有序的，因此我们可以使用二分查找来替代当前的顺序查找，因为二分查找的时间复杂度是O(logN)，而顺序查找的时间复杂度是O(n)。

由于JS没有实现二分查找，因此需要我们手动实现，而Java在Arrays.binarySearch中实现了二分查找，我们可参考其源码实现JS版的二分查找

function binarySearch(arr, key, from=0, to=arr.length) {
    let low = from
    let high = to - 1

    while(low <= high) {
        let mid = (low + high) >>> 1
        let midVal = arr[mid]

        if(midVal < key) {
            low = mid + 1
        } else if(midVal > key) {
            high = mid - 1
        } else {
            return mid
        }
    }
    return -(low + 1)
}

上面二分查找的逻辑其实很简单，每次找到范围[start, end]内中间值midVal，和目标值key比较，若相同则返回，若不同：

key > midVal，则说明目标值不可能在[start, mid]，只可能在[mid+1, end]中，因此查找范围缩小为[mid+1, end]；
ket < midVal，则说明目标值不可能在[mid, end]，只可能在[start, mid-1]中，因此查找范围缩小为[start, mid-1]；
key === midVal，说明找到了目标值得位置，就是mid

如果一直找到start > end时，还没有发现和key相等得midVal，则说明数组中不存在key。

而上面源码中，返回了 -(low+1) 作为找不到时的binarySearch返回值， -(low+1)的含义是啥呢？

而二分查找，其实就是通过双指针low,high移动，来不断缩小目标值得搜索范围，如果

如果：目标值 < 中间值，则high指针左移，变为high = mid-1，如果之后一直是目标值 < 中间值，则high会不断左移，直到high < low，此时low的位置，目标值插入数组后依旧保持数组有序的位置
如果：目标值 > 中间值，则low指针右移，变为low = mid+1，如果之后一直是目标值 > 中间值，则low会不断右移，直到low > high，此时low的位置，目标值插入数组后依旧保持数组有序的位置

由于low>=0，因此如果binarySearch在找不到值得情况下，直接返回low，那么会误导使用者，认为low得位置就是目标值在数组中得位置，为了区别，我们需要让找不到的返回值位置为负数，而low可能为0，因此为了避免出现-0的情况，返回了-(low+1)。

因此，我们可以根据binarySearch找不到目标时的返回值idx，

推导出目标值的有序插入位置：-idx-1

算法源码

/**
 * @param {number[]} nums
 * @return {number}
 */
var lengthOfLIS = function (nums) {
  const dp = [nums[0]];

  for (let i = 1; i < nums.length; i++) {
    if (nums[i] > dp[dp.length - 1]) {
      dp.push(nums[i]);
      continue;
    }

    if (nums[i] < dp[0]) {
      dp[0] = nums[i];
      continue;
    }

    const idx = binarySearch(dp, nums[i])
    if(idx < 0) dp[-(idx+1)] = nums[i]
  }

  return dp.length;
};

// 参考Java的Arrays.binarySearch实现
function binarySearch(arr, key, from=0, to=arr.length) {
    let low = from
    let high = to - 1

    while(low <= high) {
        let mid = (low + high) >>> 1
        let midVal = arr[mid]

        if(midVal < key) {
            low = mid + 1
        } else if(midVal > key) {
            high = mid - 1
        } else {
            return mid
        }
    }
    return -(low + 1)
}