在工业测量中，精度是一个复合概念，涉及到多个方面，通常用来描述测量结果的准确性和可靠性。

在选择测量仪器/传感器时，面对众多的精度名称，你是否苦恼他们具体描述的是什么精度，是否和评估要求有直接关联？

接下来，小优博士将用几个科普篇幅，详细为大家介绍优可测仪器、传感器的相关精度概念。

今天的主题是：

《常见的测量仪器/传感器的精度相关概念》

常见的测量仪器/传感器精度有：准确度、精密度、分辨率、重复性、再现性、稳定性、线性、定位精度和重复定位精度。

一、准确度（Accuracy）

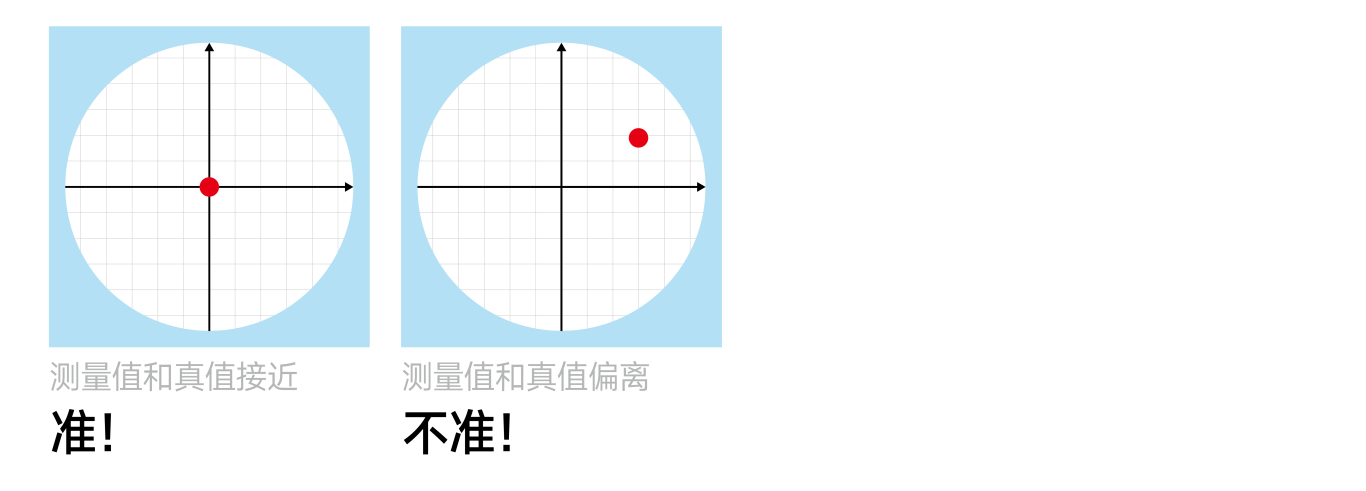
准确度是测量结果与真值或参考值之间的接近程度。

一个准确的测量结果意味着它的偏差很小，即测量值与实际值之间差异小。准确度受系统误差的影响，这些误差可能源于设备的校准、环境因素或测量方法。

二、精密度（Precision）

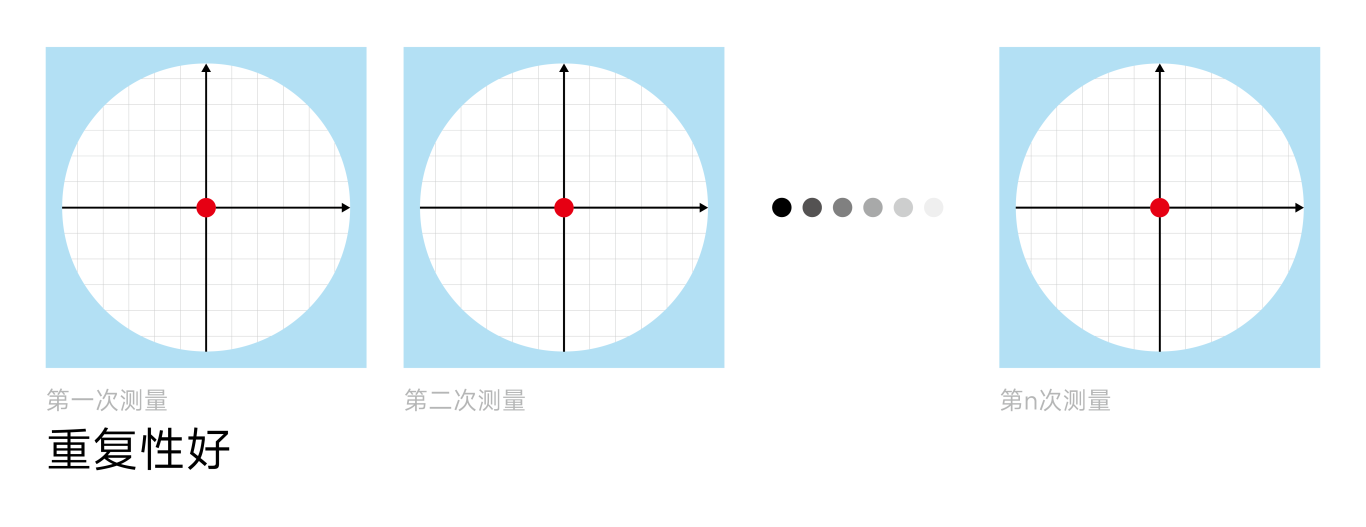
精密度描述的是重复测量结果的一致性或分散程度。

即使所有测量值都偏离了真值，只要它们彼此间差异很小，就认为这些测量具有高精密度。

三、分辨率（Resolution）

分辨率是指仪器能够区分或检测到的最小尺寸或度量单位的能力。

它是衡量测量精度的一个重要指标，影响着测量结果的准确性和可靠性。

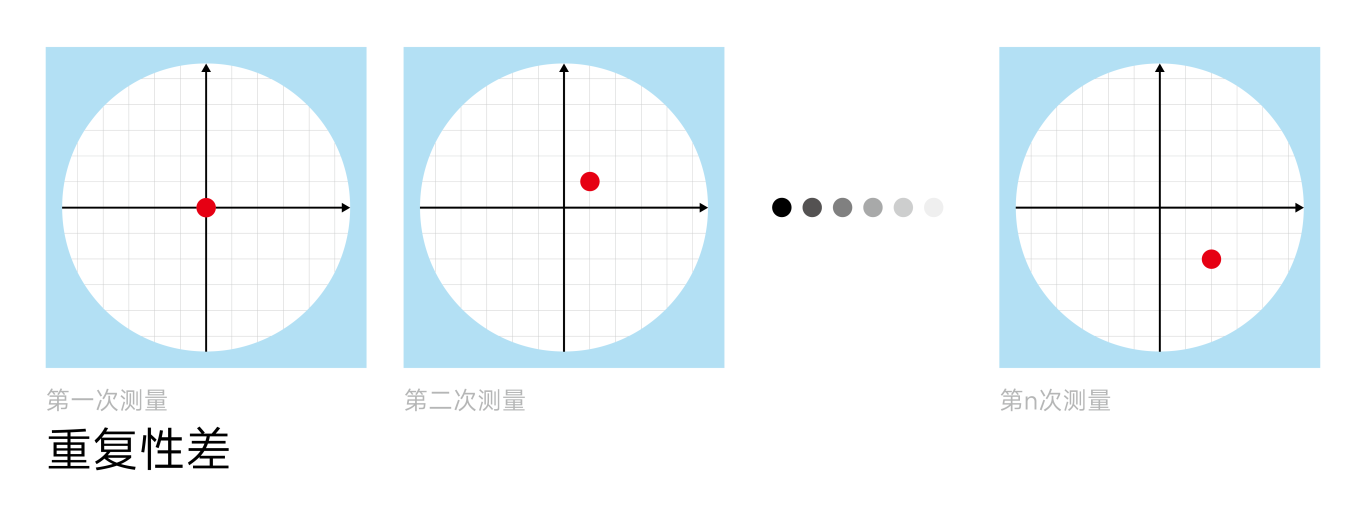
四、重复性（Repeatability）

重复性是当相同的测量在相同条件下重复进行时，获得相似结果的能力。

它关注的是在相同条件下测量的变异性。

五、再现性（Reproducibility）

再现性是指在不同的条件下（如不同的时间、操作员、同一测量系统）重复测量时，结果的一致性。

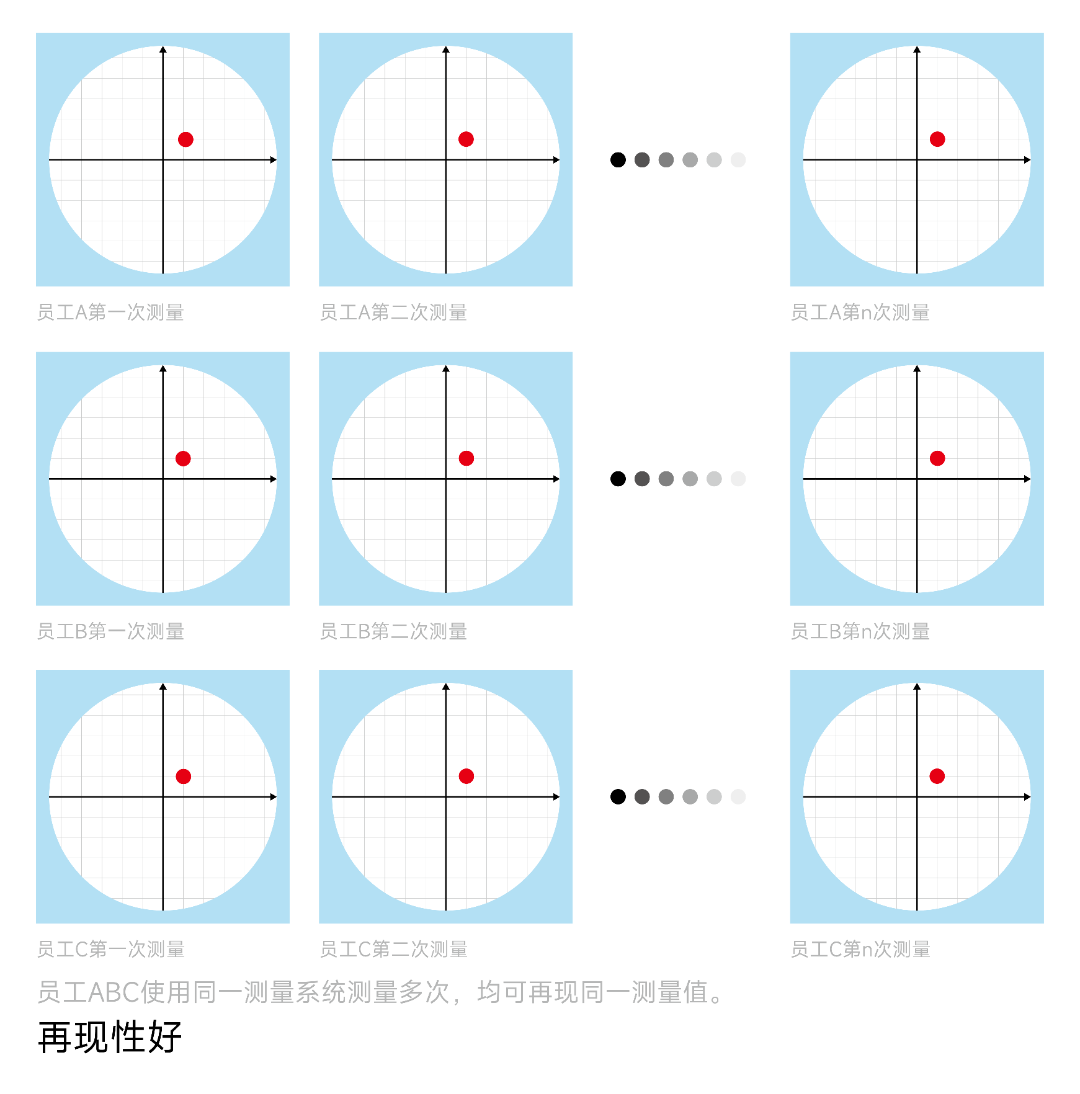
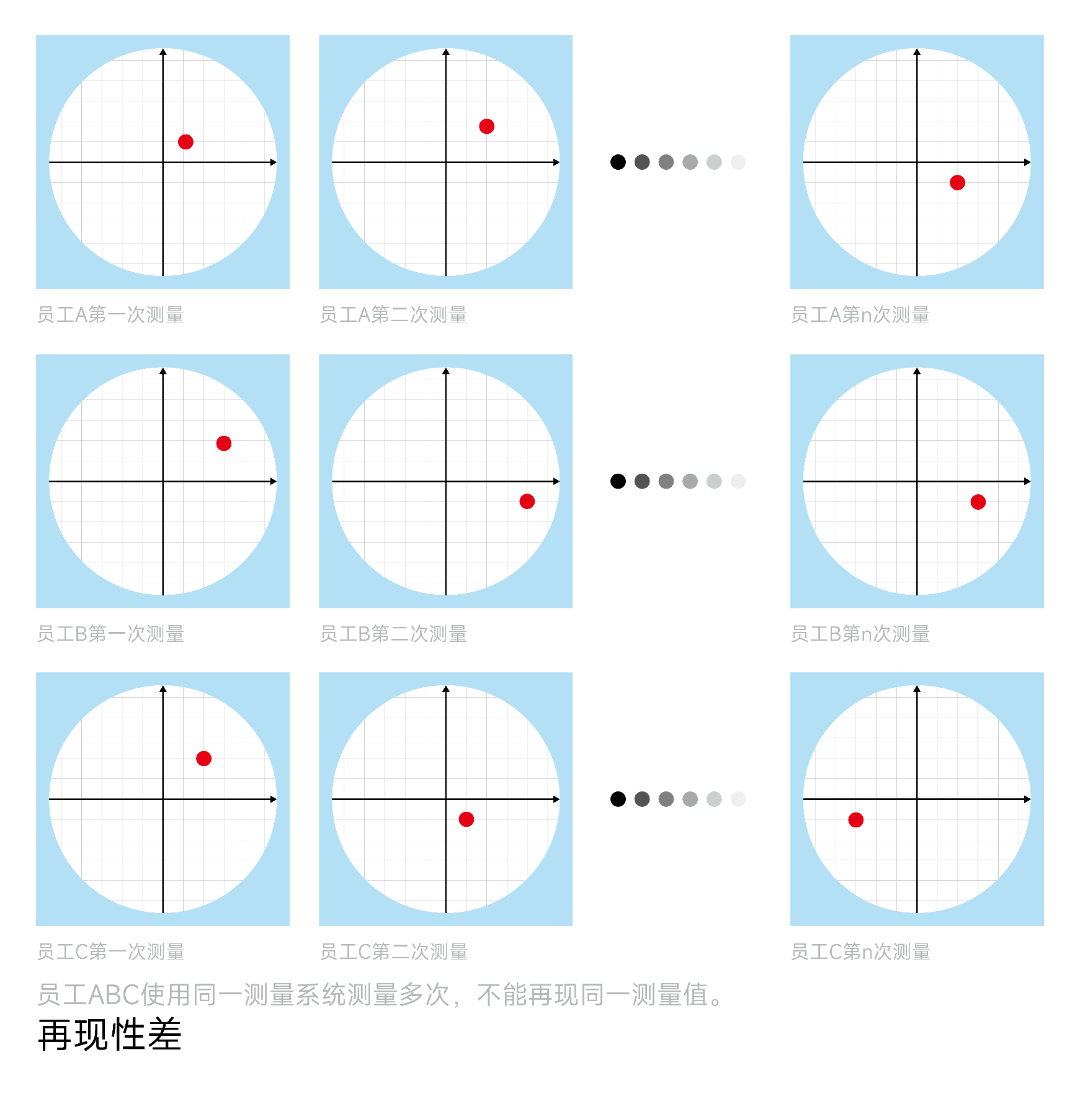
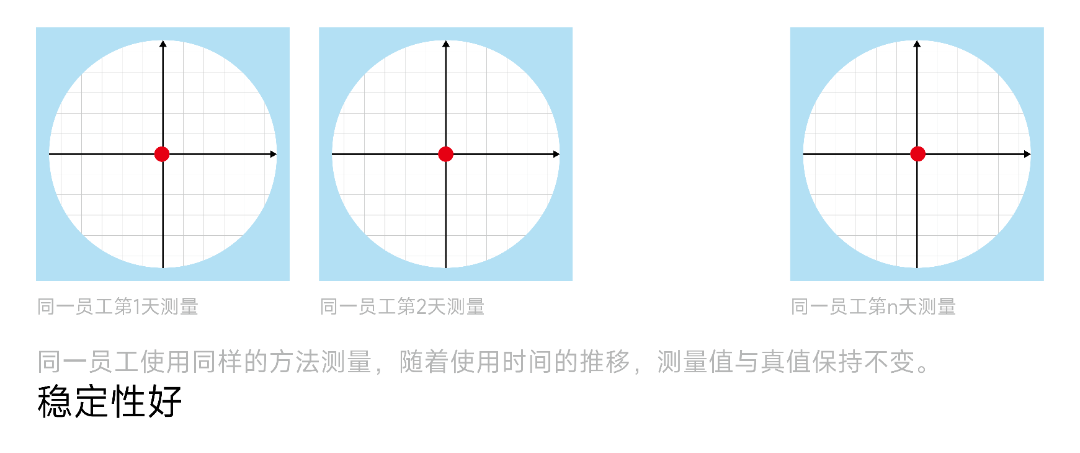
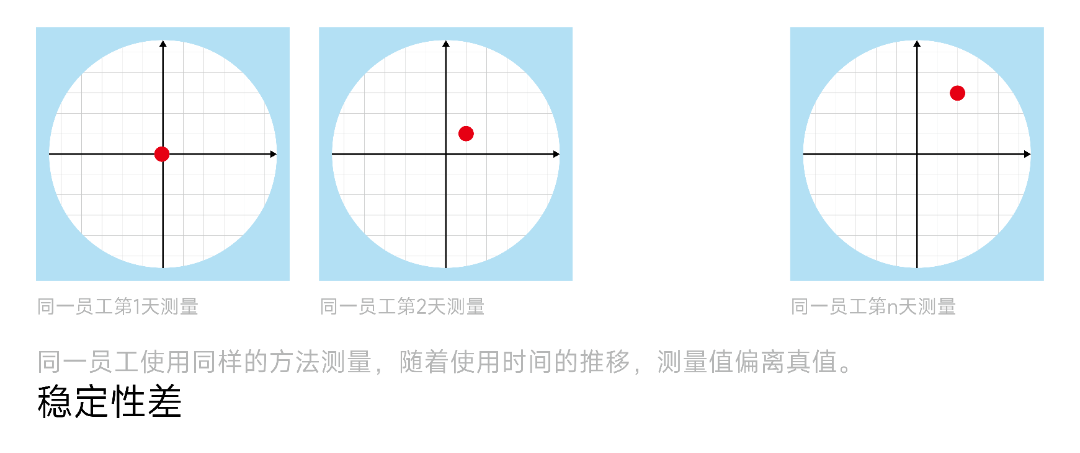
六、稳定性（Stability）

稳定性是测量系统在一段时间内保持其性能不变的能力。

设备可能会随时间而老化或漂移，从而影响测量结果。

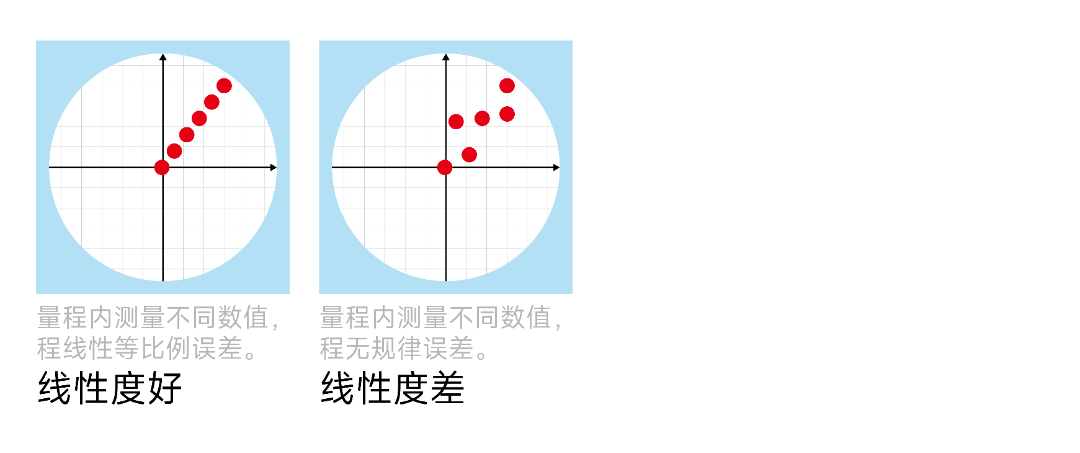
七、线性（Linearity）

线性是指测量系统在整个工作范围内，输出与输入之间的关系是否为线性的程度。

非线性可能导致在不同测量点出现不同的比例误差。

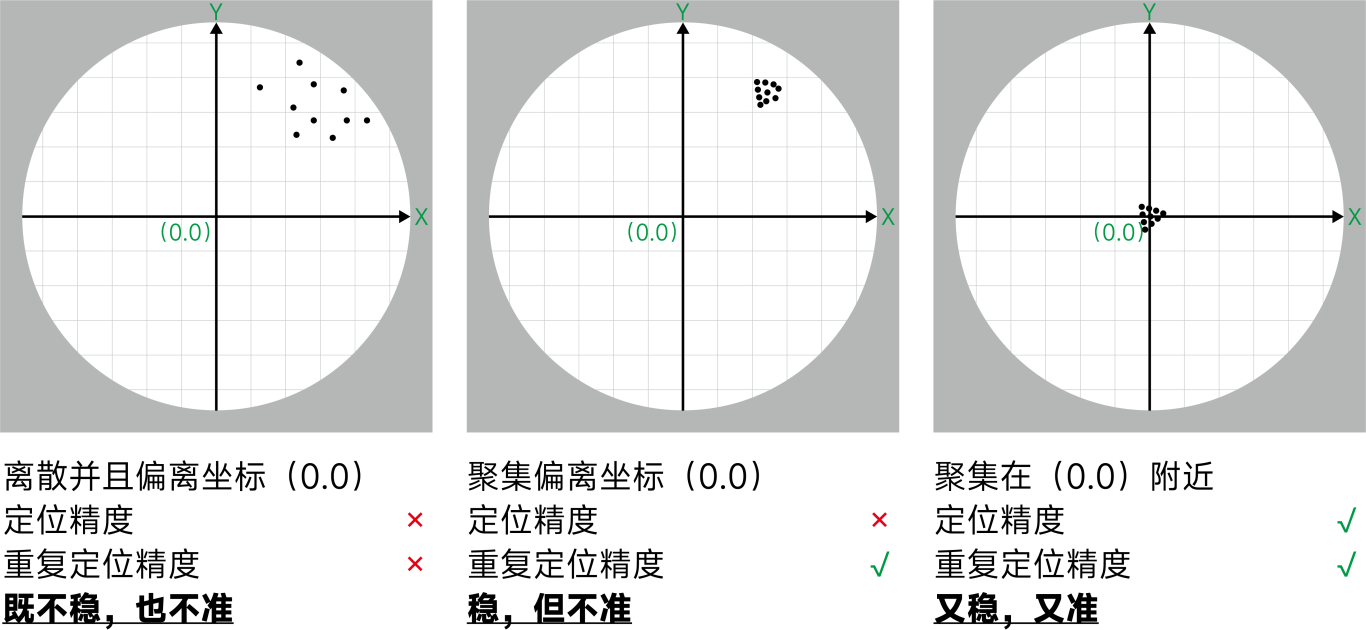
八、定位精度（Positioning Accuracy）和重复定位精度（Repeatability）

定位精度：设备移动到达实际位置与预期位置之间的差异,它是衡量设备能否准确达到指定位置的能力。 是“定位准不准”。

重复定位精度：在相同条件下，设备多次到达同一指定位置时位置偏差的一致性。它反映了设备在重复执行相同任务时的稳定性和可靠性。 是“定位稳不稳”。

下一篇，小优博士将为大家分享：

《 和白光干涉仪精度相关概念》

关注我们，敬请期待！