二分条件:
1) 序列有序 2)支持随机访问
二分思想:
大体思想是二分之后如果目标值在左侧,则中间包括右边区间所有pass掉
right = mid - 1;
目标在右侧,则中间包括左边所有pass
left = mid + 1;
注意点 left <= right
只需注意存在left 与 right 相等情况
bool Serch_Binary(vector<int> nums, int target)
int left = 0;
int right = nums.size();
while(left <= right)
{
int mid = left + (right-left)/2;
if(target < nums[mid])
right = mid - 1;
else if(target > nums[mid])
left = mid + 1;
else
return true;
}
return false;
} CSDN周赛第二十五期查找整数
一个有序数组, 2 3 4 4 4 4 7 9 23
返回target 目标值下标,如果target有重复,返回最大的下标。
#include<iostream>
using namespace std;
#include<vector>
int main()
{
int n, target;
cin>>n>>target;
vector<int> nums(n);
for(int &e : nums)
cin>>e;
int begin = 0;
int end = n-1;
int mid = -1;
while(begin<=end) // 二分查找target位置
{
mid = begin+((end-begin)/2);
if(target < nums[mid])
end = mid-1;
else if(target > nums[mid])
begin = mid+1;
else
break;
}
if(nums[mid]!=target)
{
cout<<-1<<endl;
return 0;
}
end = n-1;
begin = mid;
while(begin <= end) // 二分查找target最右边
{
mid = begin+((end-begin)/2);
if(mid == n-1)break;
if(target==nums[mid] && target != nums[mid+1])
break;
else if(target == nums[mid] && target == nums[mid+1])
begin = mid+1;
else if(target != nums[mid])
end = mid-1;
}
cout<<mid<<endl;
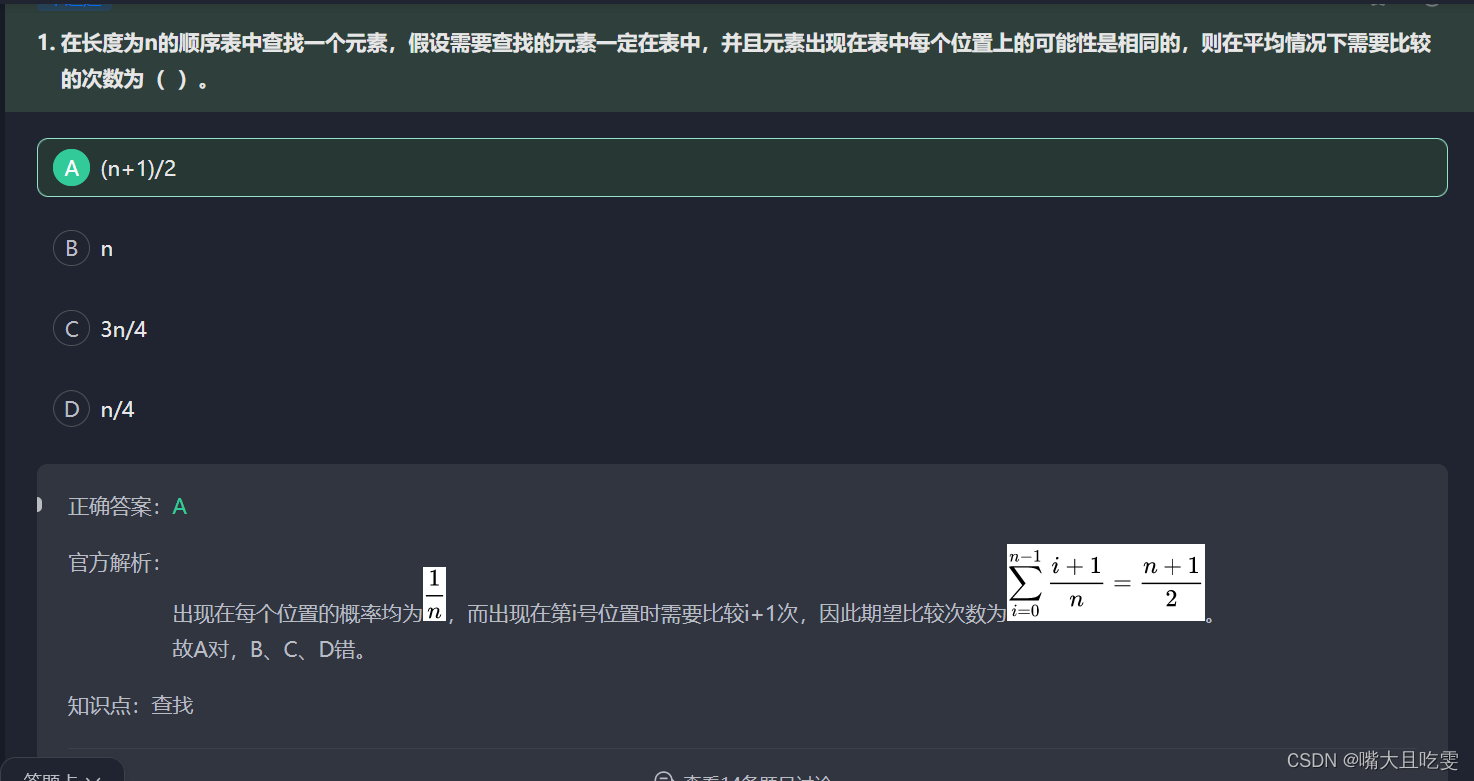
}1、二分查找中的数据元素需要满足顺序存储结构,并且有序,因为二分查找需要随机读取,所以不能使用链表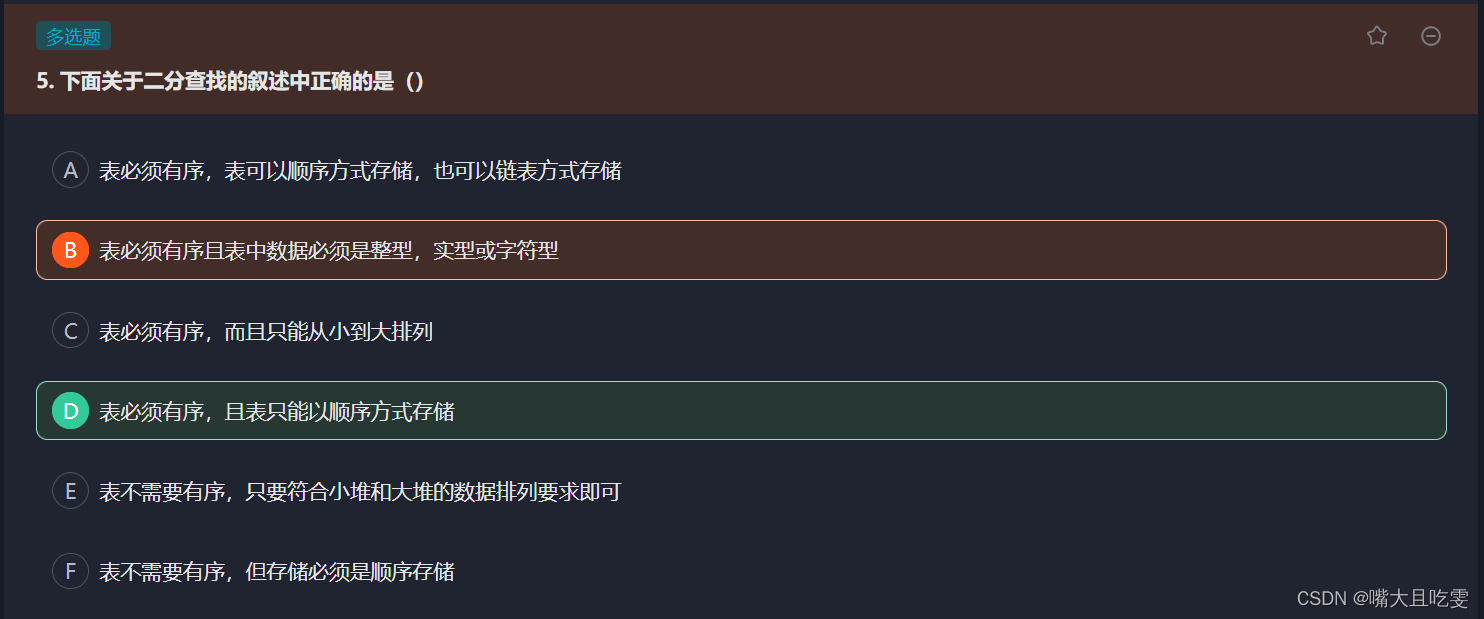
2、查找次数公式 log(N)/log(2)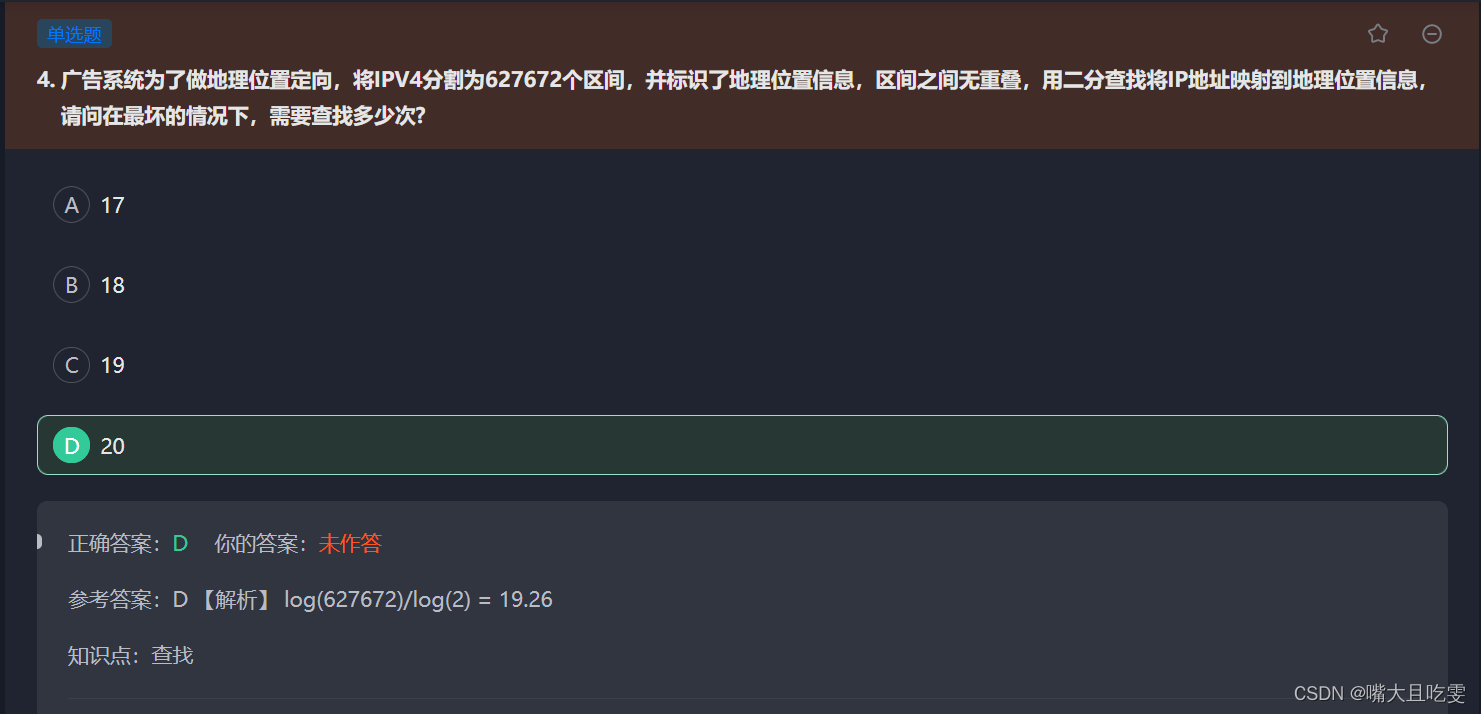
3、经典查找比较题

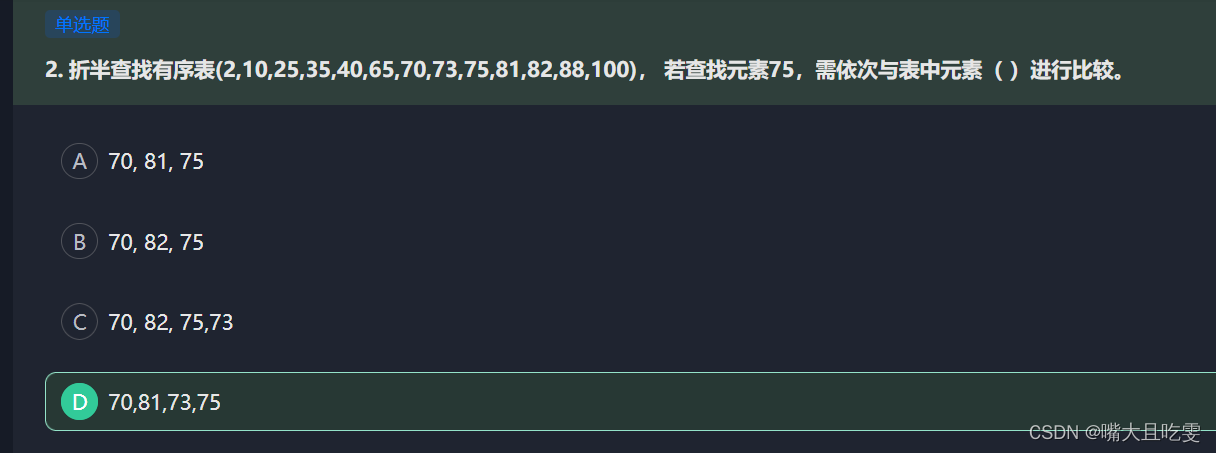
4、分块查找——二分与顺序查找的优化(块内无序,快间有序)
5、对于有N个元素的顺序表,二分查找次数的上界为logn+1
log (100) 6.65 最小次数为 6+1 = 7;
6、平均比较次数为