题目：

大概翻译：

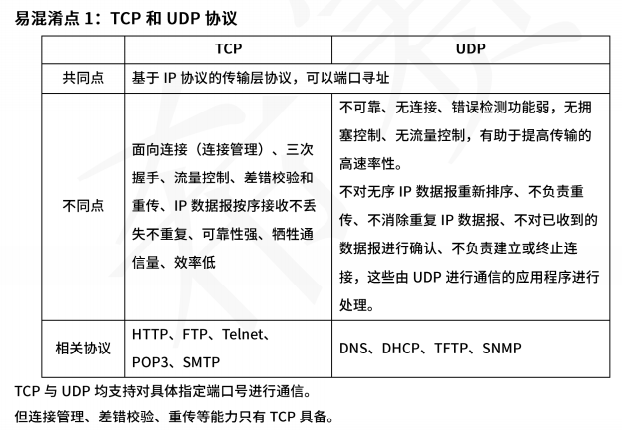
让我们把一个字符串x的f(z)函数表示为该字符串包含的不同字符数。例如，f(abc)=3。

f(bbbb) = 1, 和 f(babacaba) = 3.

给定一个字符串s，将其分成两个非空字符串a和b，使f(a)+f(b)为最大可能。换句话说，找出

换句话说，找到f(a)+f(b)的最大可能值，使a+b=s（字符串a和字符串b的连接等于字符串s）。

输入]。

输入由多个测试案例组成。第一行包含一个整数t（1<t<104）--测试案例的数量。测试用例的描述

测试用例的描述如下。

每个测试用例的第一行包含一个整数n（2 < n < 2- 10°）--字符串s的长度。

第二行包含字符串s，由小写英文字母组成。

保证所有测试案例的n之和不超过2-10°。

输出

对于每个测试案例，输出一个整数--f(a)+f(b)的最大可能值，即ata+b=s。

大致意思 ：给出一段字符串，我们要将其分为两段，我们要求这两段分别求出不重复的字符数的数量和

（这两段已经相互独立了），最大值。

大致思路：遍历所有情况;

#include <iostream>
#include <stdio.h>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector> 
#include <map>
#include <stack>
#include <queue>
#include <set>
using namespace std;
typedef long long ll;
int n, m, t, now, l, r, c, b, T, k;
const int INF = 0x3f3f3f3f;
const double pi = acos(-1.0);
int pie[] = { 3,1,4,1,5,9,2,6,5,3,5,8,9,7,9,3,2,3,8,4,6,2,6,4,3,3,8,3,2,7,9,5,0,2,8,8,4,1,9,7,1,6,9,3,9,9,3,7,5,1,0 };
int step[50][50][50];
int nx, ny, nz, ex, ey, ez;
int sum[20221199];
int w[50];
int  dp[50];
ll mod = 1e9 + 7;
string ss = "codeforces";
char p[2252225];
void check()
{
    cin >> m;//输入要遍历的字符的总值
    cin >> p + 1;
    memset(w, 0, sizeof(w));//初始化前一段的能得到的值总数
    memset(dp, 0, sizeof(dp));//初始化后一段的值的总数
    for (int i = 1; i <= m; i++)//这也属于初始化的一部分，也就是在当前位置停下分段所能的到的当前的状态
    {
        dp[p[i] - 'a'] ++;
    }
    int ans = 0;
    for (ll i = 1; i <= m; i++)//开始遍历所有的情况
    {
        w[p[i] - 'a'] ++;//在第一 , 2 , 3 , 4个停下来的话
        dp[p[i] - 'a'] --;//剩下的会剩多少
        int ans2 = 0;
        for (int j = 0; j < 26; j++)//检查前一段多少
        {
            if (w[j] != 0)
            {
                ans2++;
            }
        }
        for (int j = 0; j < 26; j++)//检查后一段有多少
        {
            if (dp[j] != 0)
            {
                ans2++;
            }
        }
        ans = max(ans2, ans);//遍历所有情况求出最大值
    }
    cout << ans << endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    while (n--)
    {
        check();
    }
    return 0;
}