环形链表

1°题目链接

链接

2°思路

slow和fast指向链表的开始
slow一次走一步
fast一次走两步
不带环 fast就会为空
带环 fast就会在环里追上slow

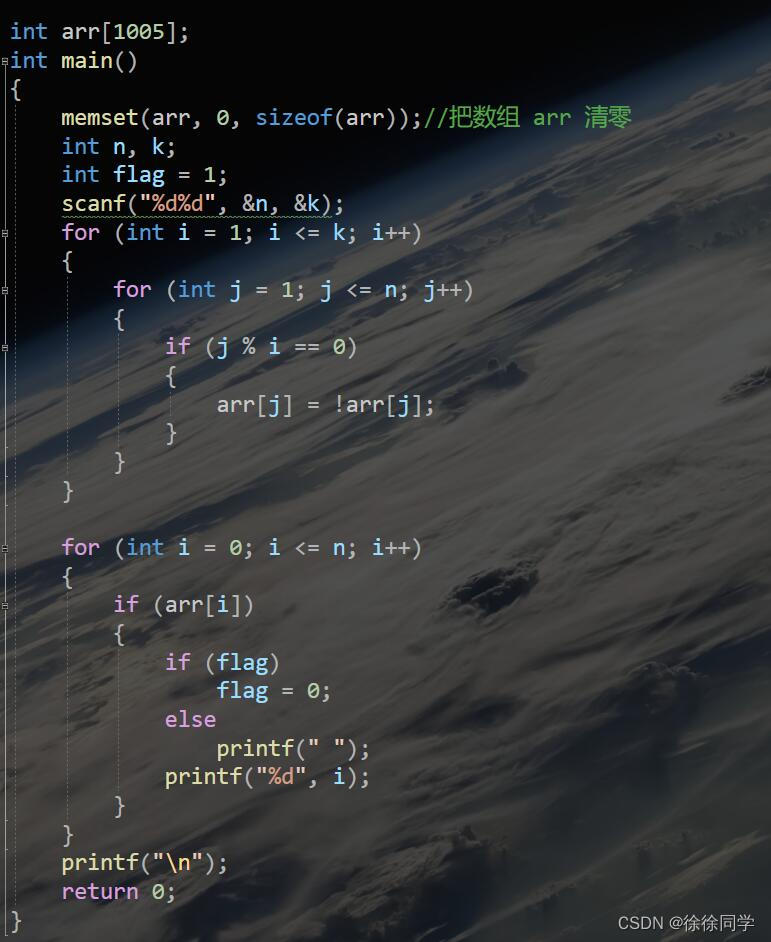
3°实现

bool hasCycle(struct ListNode* head) 
{
    struct ListNode* slow = head, * fast = head;
    while (fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast)
        {
            return true;
        }
    }
    return false;
}

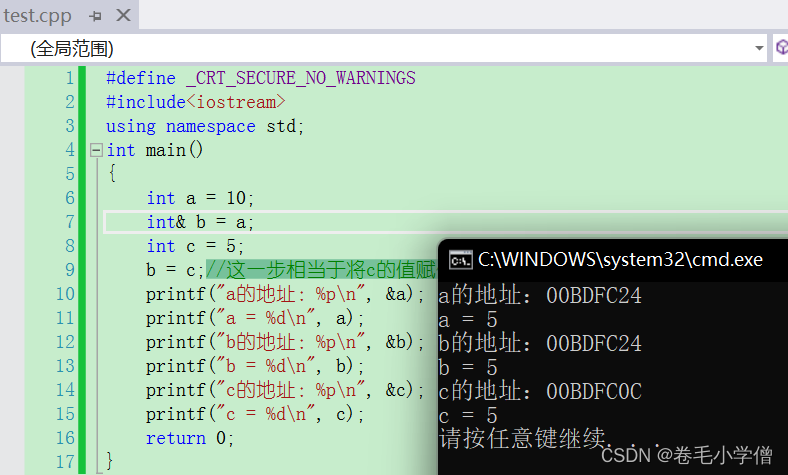
4°运行结果

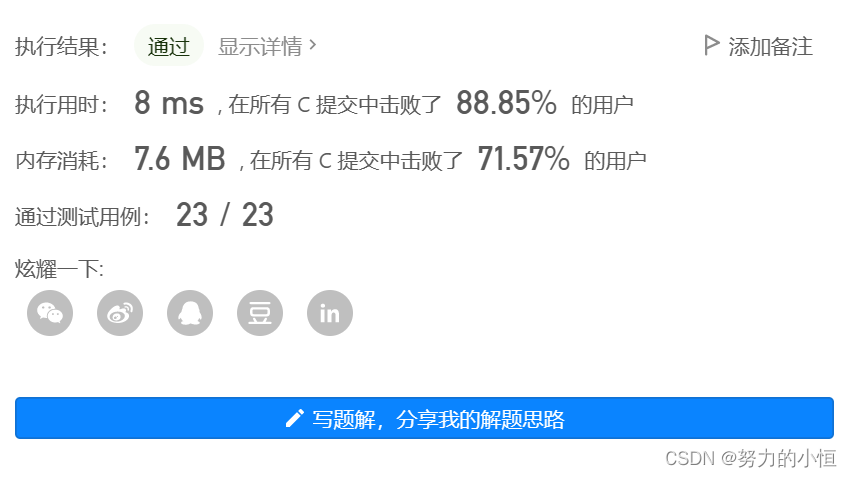
5°延伸问题

1.为什么slow和fast一定会在环中相遇?
会不会在环里面错过永远遇不上请证明一下
结论:一定会相遇但需要证明

2.为什么slow走一步 fast走的两步呢?
能不能fast一次走n步(n>2) 请证明一下
结论:fast一次走n步 n>2不一定会相遇

1.
分析证明:
第一步:slow和fast fast一定是先进环 slow走了入环前距离的一半
第二步:随着slow进环 fast已经在环里面走了一段走了多少跟环的大小一样
假设slow进环的时候 slow跟fast的距离为N
fast开始追slow slow每次走1步 fast往前走2步每追1次判断一下相遇
每追1次 fast和slow的距离变化:N会自减最后N变成0就相遇了
每追1次 距离减少1 距离最后减到0的时候就是相遇的点

2.
还是假设slow进环的时候 slow跟fast的距离为N
如果n>2的话每走一次距离缩短n-1步
N是n-1的倍数第一次可以追上
N不是n-1的倍数第一次追不上第二次有可能追上
如果第二次次再追不上就永远追不上

n=3
差为2
当N是偶数时可以追上
当N时奇数时 不可以追上 但追到最后的时候距离会变为1
再走一次变为-1 也就等价于距离变为C-1 C是环的长度
如果C-1是偶数可以追上
如果C-1是奇数永远追不上
当C-1时奇数时会重复第一次N时奇数的过程
走到最后距离又会变为C-1 死循环永远追不上

n=4
差为3
当N是3的倍数时可以追上
当N不是3的倍数时这一次不可以追上
会出现两种情况走到最后距离是2或者1
再走一步距离变为C-1或者C-2 C是环的长度
C-1或者C-2是3的倍数的话就可以追上
C-1或者C-2不是3的倍数的话就永远追不上
陷入死循环

同理的话n>2的时候有可能追不上