数据结构实验教程-第二套

news2025/1/12 7:01:19

5.一棵左子树为空的二叉树在先序线索化后，其中空的链域的个数是
a．不确定
b.0
c.1
d.2

在先序线索化之后，相当于只有开始节点没有前驱，最后的节点没有后继，因此空链域只有2个，分别是开始节点的左孩子和最后节点的右孩子。

用数组存储的线性表一定是顺序表

这个说法是错误的，链表和树也可以用数组来储存。

己知一棵树的先序序列和后序序列，一定能构造出该树。

这个说法是正确的，并且极易出错。在之前二叉树的构造中，往往都需要中序遍历再搭配先序遍历或者后序遍历才可构建二叉树，仅仅用先序和后序是无法构建二叉树的。但是仔细看会发现，本题给出的是树的先序和后序序列而非二叉树的，在对应关系中。

树	二叉树
先序遍历	先序遍历
后序遍历（后根遍历）	中序遍历

因此本题相当于是给了二叉树的先序遍历和中序遍历，是可以唯一的确定出一颗二叉树的。

直接选择排序算法是不稳定的排序算法

这个是正确的，虽然直接选择排序每次都会选出最大的元素，但在元素移动过程中涉及到swap()如( $3,3^*,1$ ) 在将1移动到第一位的过程中变为了( $1,3^*,3$ )因此是不稳定的。

6．高度为k的完全二叉树至少有_个叶子结点。

注意题目问的是至少。至多的话最后一层应该有 $2^{k-1}$ 个节点，但至少的话，最后一层只有1个节点，因此整体的叶节点应该有 $2^{k-2}$ 个。

3．对图4所示3阶B树，依次执行下列操作，画出各步操作的结果。
(1)插入90	(2)插入25	(3)插入45	(4)删除60	(5)删除80

在这里插入图片描述
具体操作过程如下:

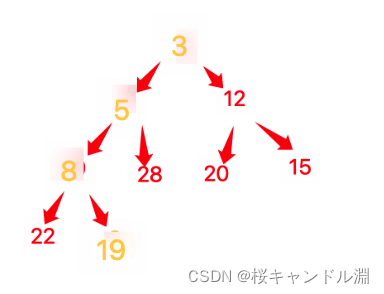
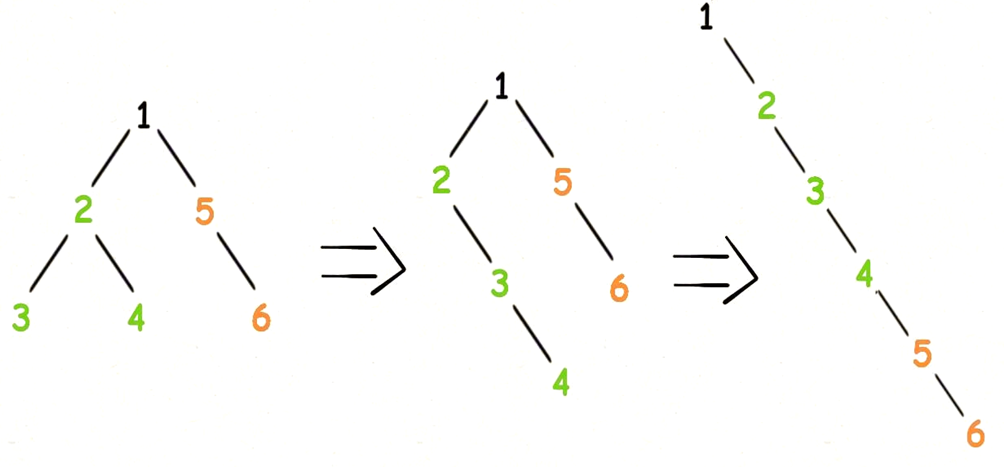
2．设计算法返回二叉树T的先序遍历序列中最后一个结点的指针，要求采用非递归形式，且不能用栈。

二叉树先序遍历的最后一个节点一定是叶节点。并且一定是最右下方的叶节点。代码如下

#include<stdio.h>
struct TreeNode {
     int val;
     struct TreeNode *left;
     struct TreeNode *right;
 };


struct TreeNode* Build(int *preorder,int p1,int p2,int *order,int o1,int o2){
    struct TreeNode *root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val = preorder[p1];
    int mid;
    for(mid = o1;order[mid]!=root->val;mid++) ;
    int llen = mid - o1;
    int rlen = o2 - mid;
    if(llen){
        root->left = Build(preorder,p1+1,p1+llen,order,o1,o1+llen-1);
    }
    else
        root->left = NULL;
    if(rlen){
        root->right = Build(preorder,p2-rlen+1,p2,order,o2-rlen+1,o2);
    }
    else
        root->right = NULL;
    return root;
}
struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
    struct TreeNode *root;
    root = Build(preorder,0,preorderSize-1,inorder,0,inorderSize-1);
    return root;
}

void LastPreNode(struct TreeNode* T){
    struct TreeNode* p = T;
    while(p->left || p->right){
        //只要还有孩子就继续往下走
        if(p->right) p = p->right;
        //优先往左走
        else p = p->left;
        //没有左孩子的话就往右下方走
    }
    printf("%d",p->val);
}
int main()
{
    int pre[] = {3,9,20,15,7};
    int in[] = {9,3,15,20,7};
    struct TreeNode* t = buildTree(pre,5,in,5);
    LastPreNode(t);
    return 0;
}

在这里插入图片描述

#include<stdio.h>

struct TreeNode {
     int val;
     struct TreeNode *left;
     struct TreeNode *right;
 };


struct TreeNode* Build(int *preorder,int p1,int p2,int *order,int o1,int o2){
    struct TreeNode *root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val = preorder[p1];
    int mid;
    for(mid = o1;order[mid]!=root->val;mid++) ;
    int llen = mid - o1;
    int rlen = o2 - mid;
    if(llen){
        root->left = Build(preorder,p1+1,p1+llen,order,o1,o1+llen-1);
    }
    else
        root->left = NULL;
    if(rlen){
        root->right = Build(preorder,p2-rlen+1,p2,order,o2-rlen+1,o2);
    }
    else
        root->right = NULL;
    return root;
}

struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
    struct TreeNode *root;
    root = Build(preorder,0,preorderSize-1,inorder,0,inorderSize-1);
    return root;
}

void Hcode(struct TreeNode* t,int k,char *code){
    //哈夫曼编码的函数
    //当前处理第k个

    if(!t) return;
    if(!t->left&&!t->right){
        printf("%4d:",t->val);
        for(int i=0;i<k;i++)
            printf("%c",code[i]);
        printf("\n");
        return;
    }

    code[k] = '0';
    Hcode(t->left,k+1,code);
    code[k] = '1';
    Hcode(t->right,k+1,code);
}
int main()
{

    int pre[] = {27,11,6,5,2,3,16,7,9,4,5};
    int in[] = {6,11,2,5,3,27,7,16,4,9,5};
    struct TreeNode* t = buildTree(pre,11,in,11);
    /*
    int pre[] = {3,9,20,15,7};
    int in[] = {9,3,15,20,7};

    struct TreeNode* t = buildTree(pre,5,in,5);
    //用先序和中序遍历建树
    */
    char code[30] = {'a'};
    Hcode(t,0,code);
    return 0;
}