在上一篇文章中,我们学习了如何将相机矩阵分解为内参矩阵和外参矩阵的乘积。在接下来的两篇文章中,我们将更详细地探讨外参矩阵和内参矩阵。首先,我们将探讨查看外参矩阵的各种方式,并在最后进行交互式演示。

SDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割
1、外参相机矩阵
相机的外参矩阵描述了相机在世界中的位置以及它指向的方向。熟悉 OpenGL 的人知道这称为“视图矩阵”(或卷入“模型视图矩阵”)。它有两个组成部分:旋转矩阵 R 和平移向量 t,但我们很快就会看到,它们并不完全对应于相机的旋转和平移。首先,我们将检查外在矩阵的各个部分,然后我们将研究更直观的描述相机姿势的其他方法。
外参矩阵采用刚性变换矩阵的形式:左侧块中为 3x3 旋转矩阵,右侧为 3x1 平移列向量:

常见的是,此矩阵的底部会添加额外的一行 (0,0,0,1)。这使得矩阵变为正方形,这使我们能够进一步将此矩阵分解为旋转和平移:
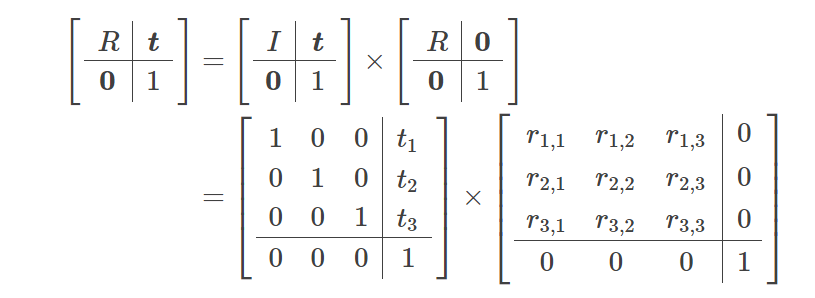
这个矩阵描述了如何将世界坐标中的点转换为相机坐标。向量 t 可以解释为相机坐标中的世界原点位置,R 的列表示相机坐标中世界轴的方向。
关于外参矩阵,需要记住的重要一点是,它描述了世界相对于相机的变换方式。这通常是违反直觉的,因为我们通常希望指定相机相对于世界的变换方式。接下来,我们将研究两种更直观的描述相机外部参数的替代方法,以及如何将它们转换为外部矩阵的形式。
2、从相机姿势构建外参矩阵
直接指定相机的姿势通常比指定世界点应如何转换为相机坐标更自然。幸运的是,以这种方式构建外部相机矩阵很容易:只需构建一个描述相机姿势的刚性变换矩阵,然后取其逆。
令 C 为描述相机中心在世界坐标中的位置的列向量,令 Rc为描述相机相对于世界坐标轴的方向的旋转矩阵。描述相机姿势的变换矩阵为 [Rc|C]。像之前一样,我们通过添加额外的一行 (0,0,0,1) 使矩阵变为正方形。然后通过反转相机的姿势矩阵获得外部矩阵:
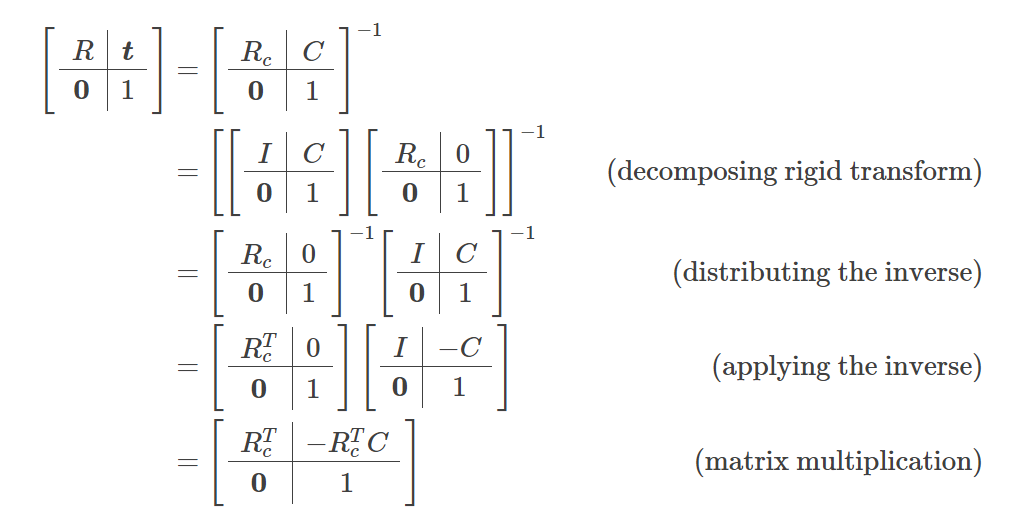
当应用逆矩阵时,我们利用旋转矩阵的逆矩阵是其转置矩阵这一事实,而平移矩阵的逆矩阵只是否定了平移向量。因此,我们看到外部矩阵参数与相机姿态之间的关系很简单:
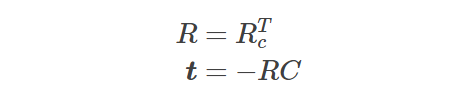
有些文本用 -RC 代替 t 来编写外部矩阵,它混合了世界变换 (R) 和相机变换符号 (C)。
3、“注视”相机
熟悉 OpenGL 的读者可能更喜欢使用第三种方式指定相机的姿势,即 (a) 相机的位置、(b) 它所注视的对象和 (c)“向上”方向。
在旧版 OpenGL 中,这是通过 gluLookAt() 函数实现的,因此我们将其称为“注视”相机。让 C 为相机中心,p 为目标点,u 为向上方向。计算旋转矩阵的算法是(摘自 OpenGL 文档):
- 计算 L = p - C。
- 标准化 L。
- 计算 s = L x u。(交叉乘积)
- 标准化 s。
- 计算 u' = s x L。
然后外部旋转矩阵由以下公式给出:
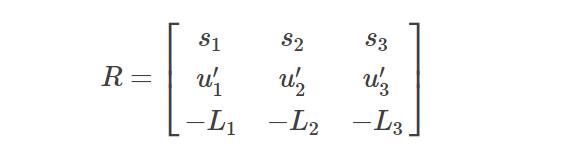
你可以像以前一样通过 t = -RC 获得平移向量。
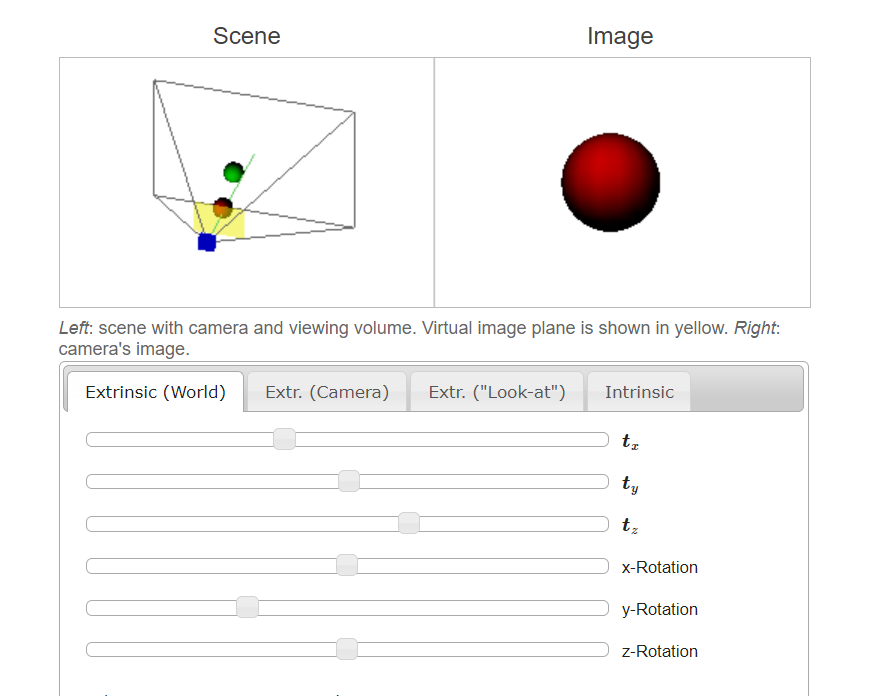
4、试试看!
以下是参数化相机外部参数的三种不同方式的交互式演示。请注意,在三种参数化之间切换时,相机的移动方式不同。
这需要启用了 WebGL 并启用了 Javascript 的浏览器。
5、结束语
我们探索了三种参数化相机外部状态的方法。你喜欢使用哪种参数化取决于具体应用程序。
如果你正在编写 Wolfenstein 风格的 FPS,可能会喜欢以世界为中心的参数化,因为沿着 (t_z) 移动总是对应于向前行走。或者你可能正在通过场景中的路径点插入相机,在这种情况下,以相机为中心的参数化是首选,因为你可以直接指定相机的位置。如果不确定你喜欢哪种,请使用上面的工具并决定哪种方法感觉最自然。
下次我们探索内参矩阵,我们将了解为什么场景的隐藏部分永远无法通过缩放相机来显示。到时候见!
原文链接:相机外参矩阵 - BimAnt