CS61C | lecture5
浮点数的表示
用一个小数点作为边界分隔整数部分和小数部分。
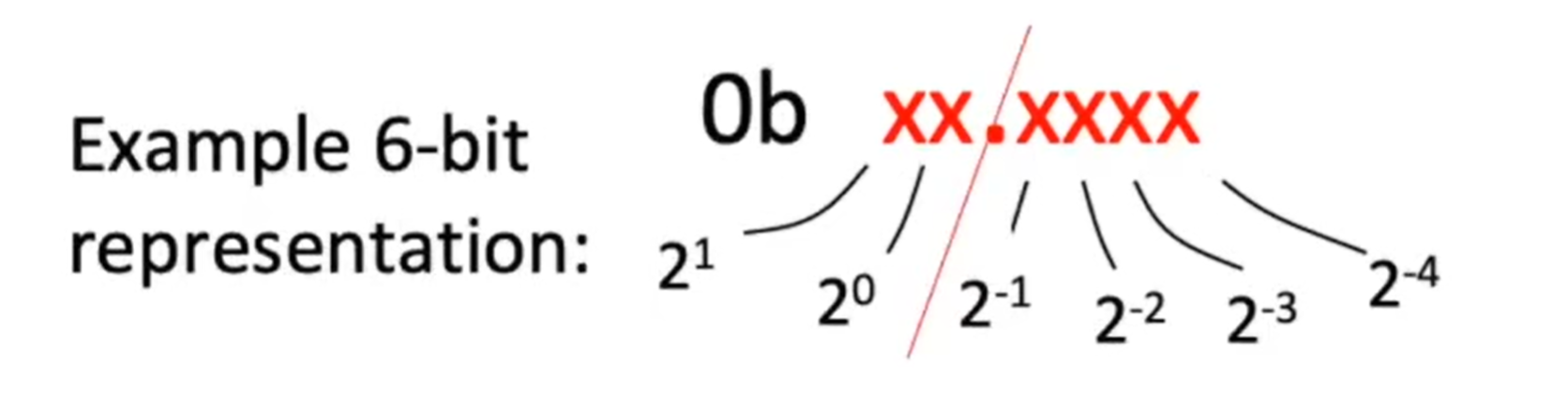
10.101
0
2
=
1
×
2
1
+
1
×
2
−
1
+
1
×
2
−
3
=
2.62
5
10
10.1010_{2}=1\times2^1+1\times2^{-1}+1\times2^{-3}=2.625_{10}
10.10102=1×21+1×2−1+1×2−3=2.62510
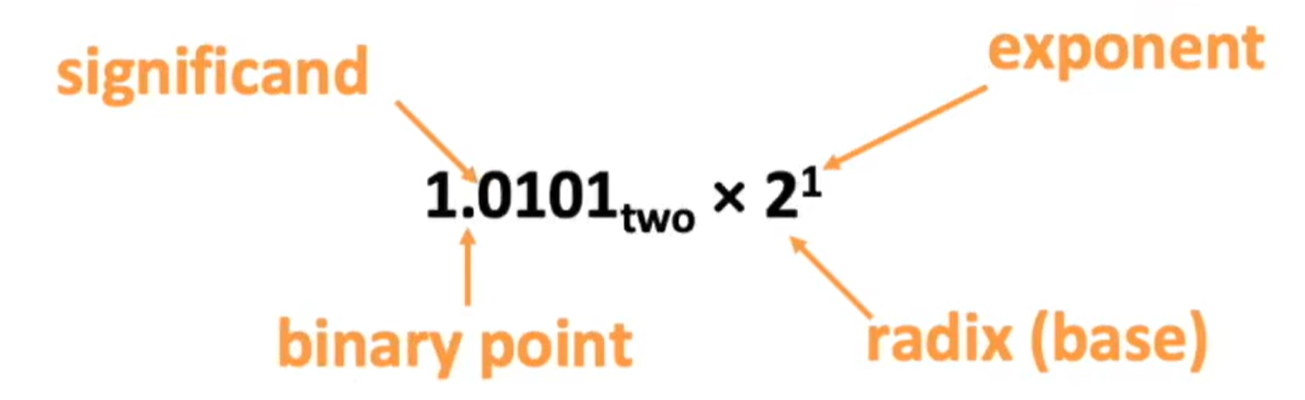
Scientific Notation(Binary)
单精度
+
1.
x
x
x
.
.
.
x
2
×
2
y
y
y
.
.
.
y
2
+{1.xxx...x_{2}\times2^{yyy...y}}_2
+1.xxx...x2×2yyy...y2

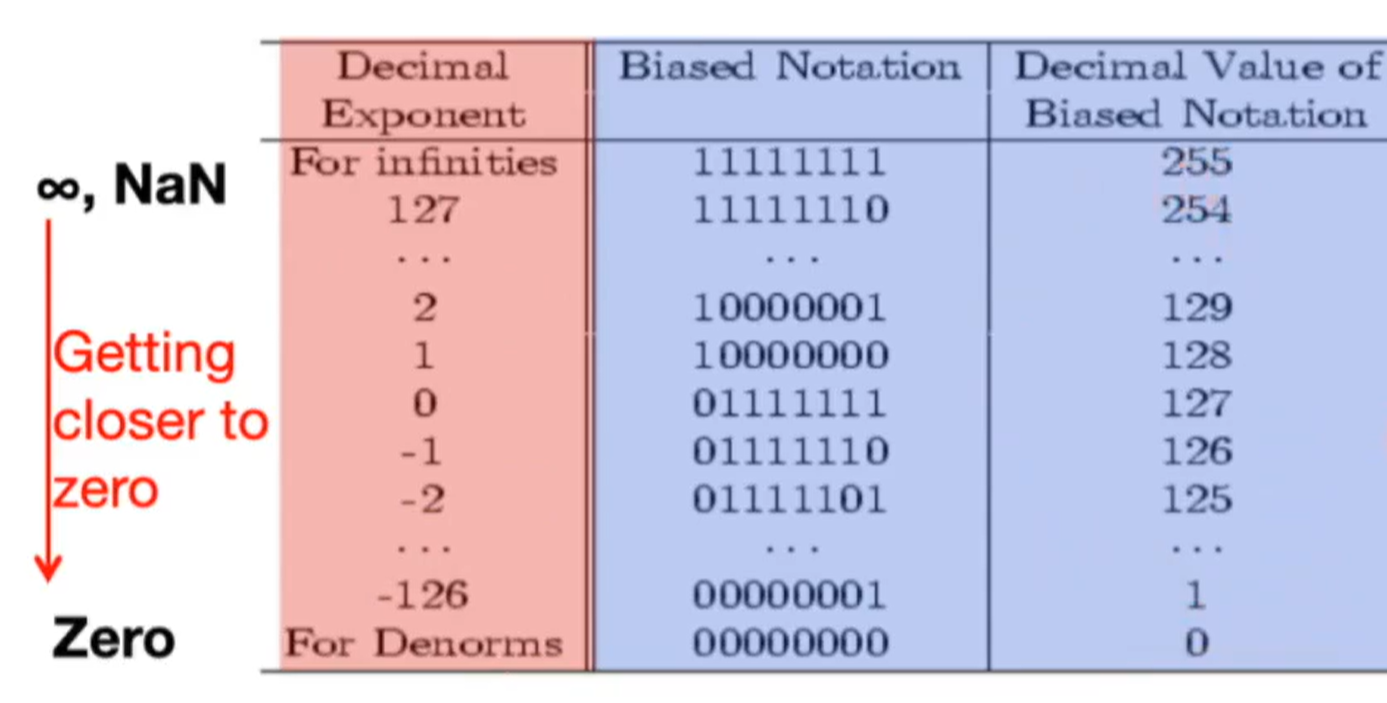
Bias = 127
(
−
1
)
S
×
(
1.
S
i
g
n
i
f
i
c
a
n
d
)
×
2
E
x
p
o
n
e
n
t
−
127
(-1)^S \times (1.\textcolor{red}{Significand})\times 2^{\textcolor{blue}{Exponent}-127}
(−1)S×(1.Significand)×2Exponent−127
0
011
1111
1
100
0000
0000
0000
0000
0000
2
=
(
−
1
)
0
×
(
1.
1
2
)
×
2
127
−
127
=
(
1.
1
2
)
×
2
(
0
)
1.
1
2
=
1
×
2
0
+
1
×
2
−
1
=
1.
5
10
\begin{aligned} &\textcolor{green}{0}\textcolor{blue}{011~~1111~~1}\textcolor{red}{100~~0000~~0000~~0000~~0000~~0000}_2 \\ =&(-1)^{\textcolor{green}{0}}\times(1.\textcolor{red}{1}_2) \times 2^{\textcolor{blue}{127} - 127} \\ =&(1.\textcolor{red}{1}_2) \times 2(\textcolor{blue}{0}) \\ \\ &1.1_2 = 1\times 2^0 + 1 \times 2^{-1} = 1.5_{10} \\ \end{aligned}
==0011 1111 1100 0000 0000 0000 0000 00002(−1)0×(1.12)×2127−127(1.12)×2(0)1.12=1×20+1×2−1=1.510
注意有一个隐式的 1 在 Significand 前面,所以是
1.
5
10
1.5_{10}
1.510 而不是
0.
5
10
0.5_{10}
0.510
双精度