北京大学：利用好不确定性，8B小模型也能超越GPT-4

大模型有一个显著的特点，那就是不确定性——对于特定输入，相同的LLM在不同解码配置下可能生成显著不同的输出。

比如问一问chatgpt“今天开心吗？”，可以得到两种不同的回答。

常用的解码策略有两种，一个是贪婪解码，即永远选择概率最高的下一个token，另一种就是采样方法，根据概率分布随机选择下一个token，常常使用温度参数平衡响应质量和多样性。

那么，这两种方式哪个更好呢？北大的一篇论文给出了答案：

贪婪解码在大多数任务中通常优于采样方法。

另外作者还发现，LLMs的这种不确定性具有巨大潜力。通过采用“Best-of-N”策略，从多个采样响应中挑选最优答案的方式，Llama-3-8B-Instruct在MMLU、GSM8K和HumanEval上均超越GPT-4-Turbo。

这是否可以说明，即使小模型单次回答可能不够准确，但多试几次，从里面挑最好的，也能找到正确答案。就像多猜几次谜语，总有一次能猜对一样。一起来看看论文中怎么说的吧~

论文标题:
The Good, The Bad, and The Greedy: Evaluation of LLMs Should Not Ignore Non-Determinism

论文链接：
https://arxiv.org/pdf/2407.10457

代码链接：
https://github.com/Yifan-Song793/GoodBadGreedy

实验设置

基准测试

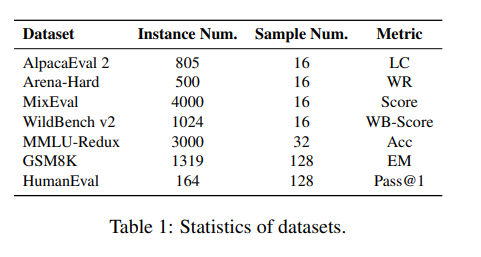
本文选择了多个基准测试如下表所示进行实验，评测模型在通用指令跟随、知识、数学推理、编码等方面的能力。

模型选择

选择开源模型Llama-3-Instruct、Yi-1.5-Chat、Qwen-2-Instruct和Mistral以及闭源模型GPT-4-Turbo作为对比。还测试了同系列中不同规模的模型，如Qwen-2和Yi-1.5。为了更深入地分析，本文还评估了使用不同对齐方法训练的模型，以研究对齐技术的效果，包括DPO、KTO、IPO、ORPO、RDPO和SimPO等对齐方法。

方法选择

本文的目标是在不同的解码配置下比较LLMs的性能。作者选择了贪婪解码和采样生成（temperature=1.0，top-p=1.0）作为主要比较。

实验结果

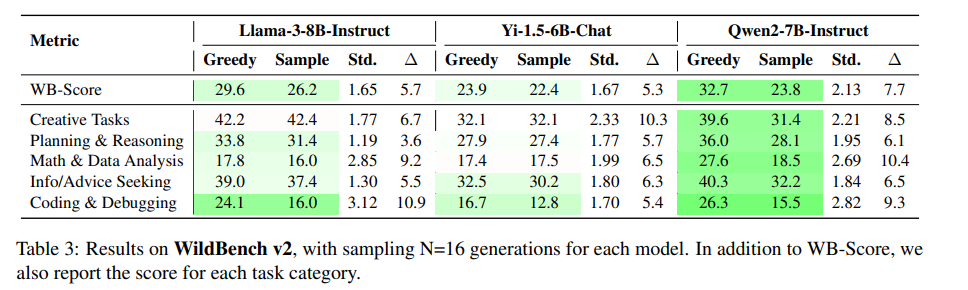
下表展示了实验结果，其中贪婪解码超过采样平均值的分数用绿色突出显示，而低于采样解码的用红色标记。

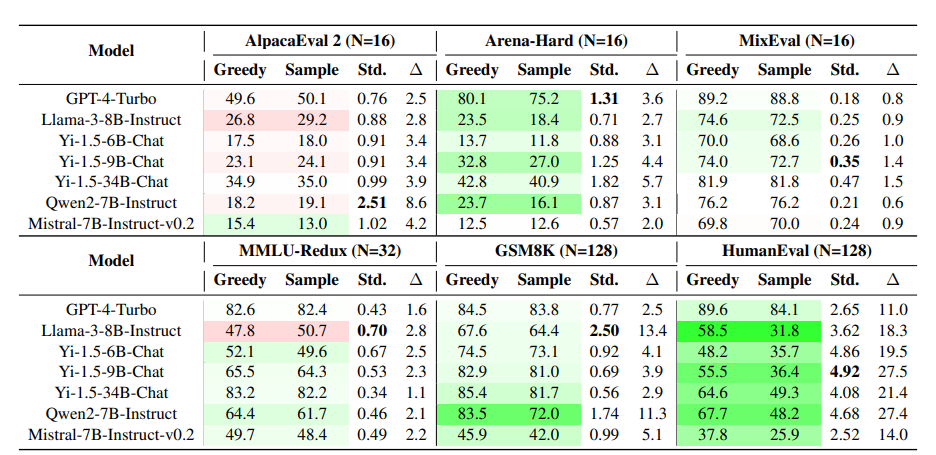
从以上结果中可以总结出一些问题的答案。

贪婪解码和采样之间的性能差距有何不同?

贪心解码和采样方法之间始终存在性能差距。这种差距在专有模型和开源模型中都很明显，并且在多个基准测试中都有体现，包括指令执行、语言理解、数学推理和代码生成。

在WildBench测试中，各任务类别的性能差距也很显著，如下表所示。不同的解码配置甚至可能改变模型排名。例如，在Arena-Hard测试中，Qwen2-7B使用贪心解码时略优于Llama-3-8B；但使用采样解码时，Llama-3-8B可能超过Qwen2-7B。

什么时候贪婪解码比采样更好，反之亦然?为什么?

对于大多数评估任务和模型，贪心解码的表现优于采样。
对于包含相对简单的开放式创意任务的AlpacaEval，采样生成的响应更好。与GSM8K和HumanEval这类需要LLM解决特定数学或编程问题的推理任务不同，AlpacaEval中50%的实例是信息查询类任务，且为开放式基准测试，没有确定的答案，其实例与难度比Arena-Hard和WildBench更简单。

哪个基准在非确定性方面最一致/最不一致?

MixEval和MMLU在稳定性上表现尤为突出，这体现在无论是使用贪心解码还是采样方法，其性能差异很小，且不同采样间的结果波动也很低。这种高度稳定性主要得益于它们答案空间的严格限制：MMLU采用多项选择题形式，而MixEval则通过真实数据基准测试要求LLM给出简短答案，从而进一步压缩了输出范围。

相比之下，GSM8K和HumanEval在处理非确定性生成任务时显得不够稳定，最佳与最差采样结果之间的性能差异可能超过10分，显示出较大的波动性。

不同模型之间的表现有何差距？

GPT-4-Turbo在多种任务上展示了稳定的性能，贪心解码与采样方法间的性能差异微乎其微，同时采样质量也有所增强。

然而，开源LLMs则展现出与众不同的特性。例如，Mistral-7B-Instruct-v0.2在AlpacaEval和Arena-Hard等开放式指令任务上，其行为模式与其他模型截然相反。同样地，Llama3-8B-Instruct在MMLU任务中，通过采样实现的性能甚至超越了贪心解码，这一表现也与众不同。

这些现象引发了对未来研究领域的深刻思考：

为何特定模型在特定任务上会展现出如此不同的行为？
这些独特性是否能为构建更稳健的LLM提供新的思路？

这些问题强调了深入探究LLM内部工作机制的重要性，这类研究有望显著提升我们对不同模型及其训练方式如何影响模型行为的理解。

各种因素如何影响非确定性?

那么各种因素又是如何影响非确定性的，这里作者调整缩放、对齐和解码参数进行实验。

Scaling对非确定性的影响

有人可能会认为，较大的LLMs在解码时的不确定性会更低，从而导致采样时的性能差异较小。但从作者的实验结果来看，并非如此。作者使用Yi-1.5-Chat和Qwen2-Instruct系列来观察从0.5B到34B参数的性能差异。

参数扩展并不会导致较低的采样方差。Qwen2-7B-Instruct在AlpacaEval和HumanEval上的方差高于其较小的对应模型。并且不同大小的模型在不同任务上的性能差异显著，无法得出统一的结论。

对齐对非确定性的影响

对齐方法（如DPO）通过学习偏好数据来增强LLM。作者使用Llama-3-8B-Instruct作为训练起点，评估了DPO、KTO和SimPO等对齐方法的效果。如下图所示，应用这些方法后，贪婪解码和采样性能均受到影响。

在AlpacaEval、MMLU、GSM8K和HumanEval等任务中，标准差有所下降，这表明对齐可能会减少采样输出的多样性。然而，需注意，并非所有对齐方法都能始终如一地提高模型性能。例如，KTO和SimPO在MMLU上导致性能下降。此外，SimPO在MixEval基准上效果有限。

温度对非确定性的影响

对于采样生成，温度控制采样过程的随机性，较低的值使模型更具确定性，而较高的值使模型更随机。作者评估不同温度对非确定性生成的影响。

如上图所示，在AlpacaEval任务中，较高的温度会略微提高性能。在多项选择题的问答任务中，温度变化对性能的影响不显著。

值得注意的是，当温度极端升高至如1.5时，LLM在需要推理和代码生成的任务（如GSM8K和HumanEval）上显著受阻，模型解答问题变得困难。相反，在开放式指令任务（如AlpacaEval和ArenaHard）中，即便温度较高，模型依然能保持相对良好的表现。

重复对生成的影响

除了控制贪婪搜索和采样的参数，还有一个关键参数——重复惩罚，它也会影响生成过程。

重复惩罚通过调整新词是否重复出现在提示和已生成文本中的概率来工作。具体来说，值大于1.0时，模型倾向于使用更多新词；小于1.0时，则促进词语的重复。默认情况下，该参数设为1.0，以保持平衡。

如上图所示，大多数情况下建议保持默认值以获得最佳性能。但在AlpacaEval任务中，略微提高重复惩罚（如1.2）可能因GPT评审偏好简短答案而带来性能提升。

对于MixEval和MMLU，由于都鼓励简洁输出，重复惩罚的影响较小。而GSM8K数学推理任务则不同，最佳表现出现在重复惩罚设为0.9时，因数学推理常需重复问题中的数字和条件，过高设置反而降低性能。

非确定性生成中的表面模式

作者还对比了不同生成配置下各类任务的生成长度。如下图所示，贪心解码产生的响应比采样平均值短的情况用蓝色突出显示，反之则用紫色标记。

可以观察到贪婪解码生成的文本通常比采样生成的略短。在Yi系列模型处理AlpacaEval和GSM8K任务时，这一模式出现了变化，两种生成方法产生的响应长度几乎相当。

下图展示了Qwen2-7B-Instruct在GSM8K上贪婪解码与采样生成的效果差异。

结果显示，贪婪解码在解决GSM8K问题上表现显著优于采样生成（83.5% vs. 72.0%）。贪婪解码能有效且准确地解答问题，而采样生成则在多次尝试中错误率激增，达到89%，这表明采样方法可能在一定程度上削弱了LLMs的推理能力。

LLMs的不确定性有何潜力

当前对LLMs的评估常局限于单一输出，这限制了对其全面能力的洞察。作者采用“Best-of-N”策略，即从多个采样响应中挑选最优答案。利用ArmoRM和FsfairX等先进奖励模型，对Llama-3-8B-Instruct的响应进行评分并排序，选取最高分作为输出。同时，设立“oracle”基准，以最佳响应为上限，评估策略潜力。

可以看到“Best-of-N”策略极大提升了LLMs性能，尤其是oracle选择下，Llama-3-8B-Instruct在MMLU、GSM8K和HumanEval上均超越GPT-4-Turbo。这凸显了小规模LLMs的强劲实力。

因此未来可以从两条路径强化小规模LLMs：