力扣刷题之3111.覆盖所有点的最少矩形数目

news2024/9/22 13:40:01

题干描述

给你一个二维整数数组 point ，其中 points[i] = [xi, yi] 表示二维平面内的一个点。同时给你一个整数 w 。你需要用矩形 覆盖所有 点。

每个矩形的左下角在某个点 (x1, 0) 处，且右上角在某个点 (x2, y2) 处，其中 x1 <= x2 且 y2 >= 0 ，同时对于每个矩形都必须满足 x2 - x1 <= w 。

如果一个点在矩形内或者在边上，我们说这个点被矩形覆盖了。

请你在确保每个点都至少被一个矩形覆盖的前提下，最少需要多少个矩形。

注意：一个点可以被多个矩形覆盖。

示例 1：

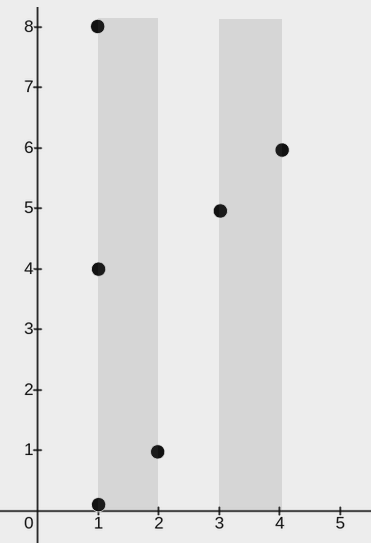
输入：points = [[2,1],[1,0],[1,4],[1,8],[3,5],[4,6]], w = 1

输出：2

解释：

上图展示了一种可行的矩形放置方案：

一个矩形的左下角在 (1, 0) ，右上角在 (2, 8) 。
一个矩形的左下角在 (3, 0) ，右上角在 (4, 8) 。

示例 2：

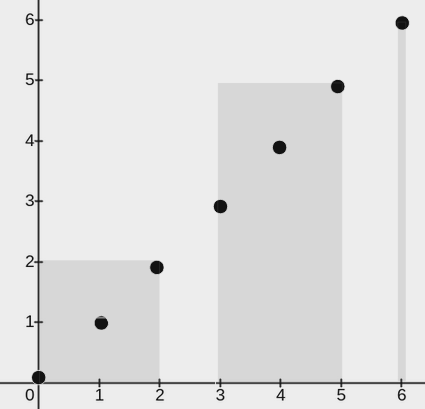
输入：points = [[0,0],[1,1],[2,2],[3,3],[4,4],[5,5],[6,6]], w = 2

输出：3

解释：

上图展示了一种可行的矩形放置方案：

一个矩形的左下角在 (0, 0) ，右上角在 (2, 2) 。
一个矩形的左下角在 (3, 0) ，右上角在 (5, 5) 。
一个矩形的左下角在 (6, 0) ，右上角在 (6, 6) 。

示例 3：

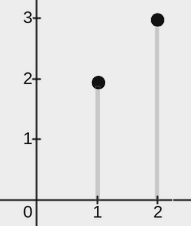
输入：points = [[2,3],[1,2]], w = 0

输出：2

解释：

上图展示了一种可行的矩形放置方案：

一个矩形的左下角在 (1, 0) ，右上角在 (1, 2) 。
一个矩形的左下角在 (2, 0) ，右上角在 (2, 3) 。

题干分析

题干解析

我们需要用矩形覆盖所有二维平面上的点，每个矩形的宽度不超过w。目标是找到覆盖所有点所需的最少矩形数量。

解题思路

1.排序：

首先按照x坐标对点进行排序，以方便后续操作。

2.贪心算法：

我们使用贪心算法，尽量用最少的矩形覆盖尽可能多的点。

从左到右遍历点，每次尽量扩展矩形的右边界，使其覆盖尽可能多的点。
如果当前点的x坐标超出了当前矩形的右边界，则需要新增一个矩形。

3.代码实现

#include <stdio.h>
#include <stdlib.h>

// 比较函数，用于qsort排序
int compare(const void* a, const void* b) {
    return (*(int**)a)[0] - (*(int**)b)[0];
}

/**
 * 函数：找到覆盖所有点所需的最少矩形数量
 * @param points: 二维整数数组，表示每个点的坐标
 * @param pointsSize: 数组points的大小
 * @param pointsColSize: 数组points每一行的大小
 * @param w: 矩形的最大宽度
 * @return: 返回最少的矩形数量
 */
int minRectanglesToCoverPoints(int** points, int pointsSize, int* pointsColSize, int w) {
    // 对点按x坐标进行排序
    qsort(points, pointsSize, sizeof(int*), compare);
    
    int rectangles = 0;
    int bound = -1; // 当前矩形的右边界
    
    for (int i = 0; i < pointsSize; i++) {
        // 如果当前点的x坐标超过当前矩形的右边界，说明需要新的矩形
        if (points[i][0] > bound) {
            bound = points[i][0] + w;
            rectangles++;
        }
    }
    
    return rectangles;
}

int main() {
    // 示例 1
    int points1[][2] = {{2,1},{1,0},{1,4},{1,8},{3,5},{4,6}};
    int* points1Ptrs[6];
    for (int i = 0; i < 6; i++) points1Ptrs[i] = points1[i];
    int pointsSize1 = 6;
    int pointsColSize1 = 2;
    int w1 = 1;
    printf("示例 1 结果: %d\n", minRectanglesToCoverPoints(points1Ptrs, pointsSize1, &pointsColSize1, w1));

    // 示例 2
    int points2[][2] = {{0,0},{1,1},{2,2},{3,3},{4,4},{5,5},{6,6}};
    int* points2Ptrs[7];
    for (int i = 0; i < 7; i++) points2Ptrs[i] = points2[i];
    int pointsSize2 = 7;
    int pointsColSize2 = 2;
    int w2 = 2;
    printf("示例 2 结果: %d\n", minRectanglesToCoverPoints(points2Ptrs, pointsSize2, &pointsColSize2, w2));

    // 示例 3
    int points3[][2] = {{2,3},{1,2}};
    int* points3Ptrs[2];
    for (int i = 0; i < 2; i++) points3Ptrs[i] = points3[i];
    int pointsSize3 = 2;
    int pointsColSize3 = 2;
    int w3 = 0;
    printf("示例 3 结果: %d\n", minRectanglesToCoverPoints(points3Ptrs, pointsSize3, &pointsColSize3, w3));

    return 0;
}