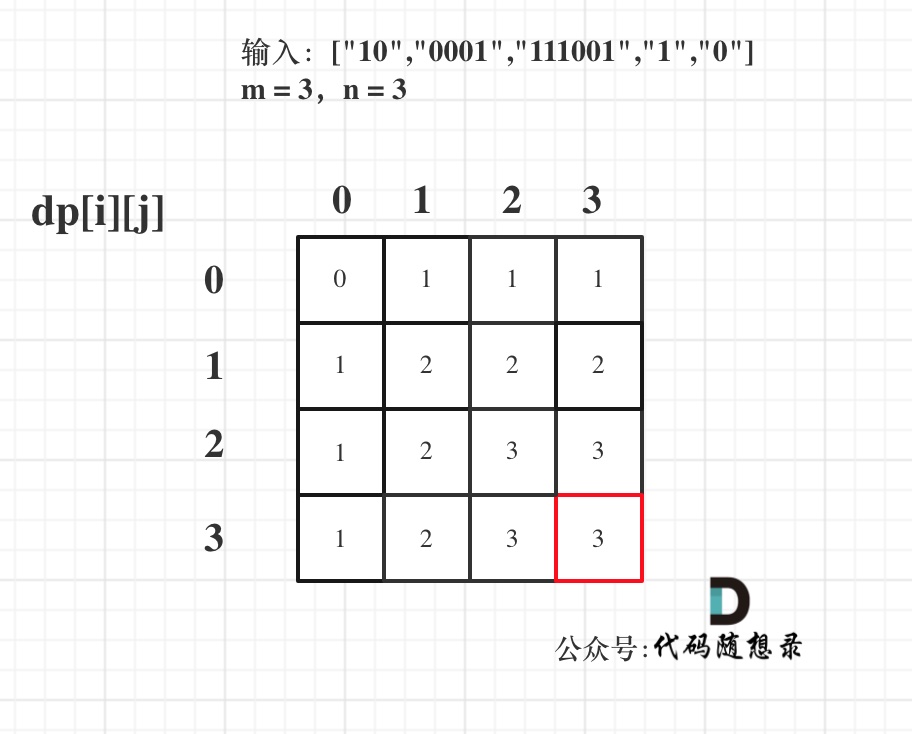
一.绪论:

二.数据结构(二叉树):
1.简介:

1)每一个节点(也叫结点)都是一个独立的对象-->当中不仅要存数据值,还要存父节点地址值,左子节点地址值,右子 节点地址值

2)没有父节点或者子节点的节点就记为null



2.遍历方式:(适用于所有二叉树)
a.前序遍历:按照上->中->下的方式遍历

b.中序遍历:(重点)按照左->中->右的方式遍历(也是按小到大)

c.后序遍历:

d.层序遍历:

3.遍历方式的总结:

三.数据结构(二叉查找树):
1.概念:

2.添加节点:
规则:

3.查找结点:
要从根节点*开始查找,之后根据小的在左边,大的在右边进行查找即可
四.数据结构(平衡二叉树):
1.规则:

该二叉树不是平衡二叉树,因为比如节点10的左子树高度为0,节点10的右子树高度为3,高度差为2,已经超过了1
注:规则中的任意节点是指同一个节点的左右子树,不是任意两个节点
2.实例:

该二叉树是平衡二叉树
节点7的左子树高度为2,右子树高度为1,高度差为1,符合规则
其他节点同理
五.数据结构(树)的演变:

六.平衡二叉树的旋转机制->用于保持二叉树的平衡:(平衡时不用旋转)
1.规则1->左旋:

例1:

改正后为:

例2:



2.规则2->右旋:

例1:


例2:



3.触发时机:当添加一个节点后,该树不再是一颗平衡二叉树(如果添加一个节点后仍旧是平衡二叉树,则不触发旋转机制)
七.平衡二叉树需要旋转的四种情况:
1.左左:当根节点左子树的左子树有节点插入,导致二叉树不平衡(一次右旋即可搞定)
例如:

插入节点后:

改正:

2.左右:当根节点左子树的右子树有节点插入,导致二叉树不平衡(不止一次才能搞定->
先局部左旋,再整体右旋)
例如:

插入节点后:

开始旋转:


但仍未平衡,继续旋转:
先要重新进行局部旋转




3.右右:当根节点右子树的右子树有节点插入,导致二叉树不平衡(一次左旋即可搞定)
例如:

添加节点后:



4.右左:当根节点右子树的左子树有节点插入,导致二叉树不平衡(不止一次才能搞定->
先局部右旋,再整体左旋)
例如:

添加节点后:

开始旋转: