页式存储和段氏存储会考
页式存储几乎必考，段氏存储可能会考

页式存储

页式存储是操作系统的一种存储管理方式。

因为我们的程序往往是远远大于内存的，所以程序在执行的时候，是不会一次性把所有内容都装入到内存中，它会把程序分为若干个页，每个页固定大小，一般是4K,然后把这些页离散存入到内存中，而内存是按块来划分的，所以就通过页表来进行映射程序中的页在内存中的块的存储；

比如：游戏有10G，内存只有4G。10G的程序这么分配到4G的内存中去的？玩游戏的时候，并不是一开始就将所有的东西都展示出来，都是根据场景，打怪，位置等分析所需的资源，然后把需要的资源放到内存中使用。怎么将数据放到内存中去的？将程序分成若干个页，我们程序员写游戏的时候，需要定义一些变量，有些变量代表图片资源，有些代码音频资源，视频资源，还有一些简单的数据。这些数据在写代码的时候是有地方存储的，这个地方就做逻辑地址。

进程（程序）中的地址，我们称之为逻辑地址（虚地址），而内存中的地址我们称之为物理地址（实地址）；

每个页分为页号和页内地址，页号用来和块号对应，代表存储的位置，大小可以代表页的数量，页内地址代表的是存储的数据内容，大小可以代表数据大小

优点：利用率高、碎片小（只在最后一个页中有）、分配及管理简单。
缺点：增加了系统开销，可能产生抖动现象。

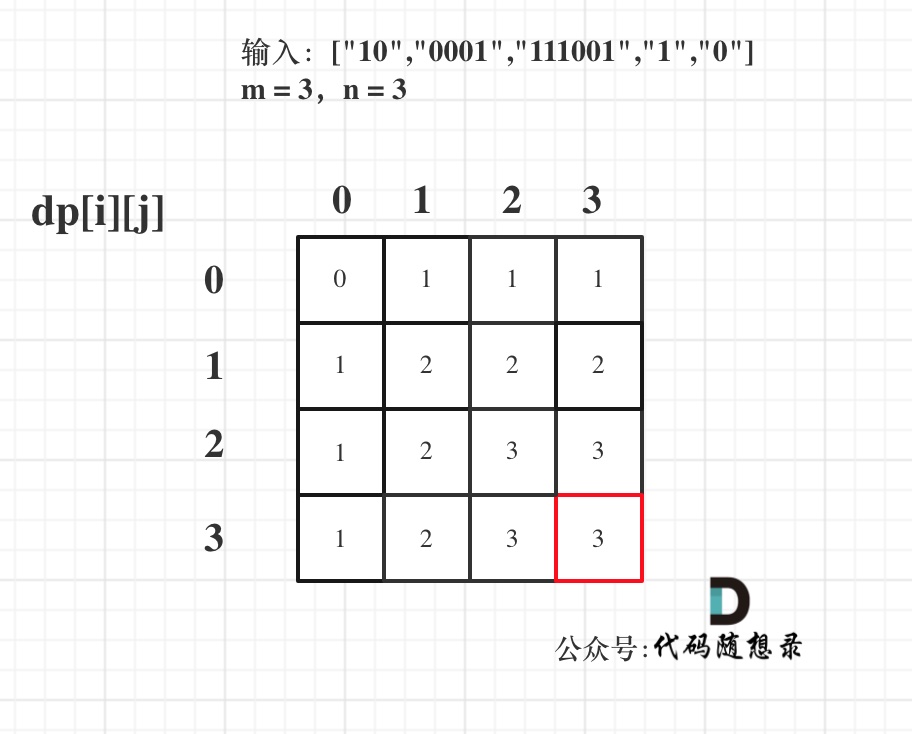
例如：将100K的数据存储到内存里，按照4K/页，那么25页就能存完。
但是103K的数据存到内存里，最后一页没有存完，只存储了3K，还剩余1K，这就是碎片

练习题

【2021架构】某计算机系统页面大小为4K,若进程的页面变换表如下所示，逻辑地址为十六进制1D16H。该地址经过变换后，其物理地址应为十六进制(26)

A.1024H
B.3D16H
C.4DI6H
D.6D16H

答案B
页表=页号+页内地址
快速做题技巧：
1D16H：第一位1基本上就是页号，最后一位H是单位。D16是页内地址，看图页号1对应块号是3。所以答案是B
计算方法：
将十六进制数1D16H转换成二进制数 0001 1110 0001 0110
4K=2¹²，所以取二进制数的后12位为页内地址，前4位则为页号地址0001=1，由图可知跳转到物理块号为3的地方
也可以这么计算：4K=4096=2¹²=(2⁴)³，2⁴=16正好是一个16进制的位，所以1D16后3位是页内地址

页式置换算法

有时候，进程空间分为100个页面，而系统内存只有10个物理块，无法全部满足分配，就需要将马上要执行的页面先分配进去，而后根据算法进行淘汰，使100个页面能够按执行顺序调入物理块中执行完。
缺页表示需要执行的页不在内存物理块中，需要从外部调入内存，会增加执行时间，因此，缺页数越多，系统效率越低。

• 最优算法：OPT,理论上的算法，无法实现，是在进程执行完后进行的最佳效率计算，用来让其他算法比较差距。原理是选择未来最长时间内不被访问的页面置换，这样可以保证未来执行的都是马上要访问的。
• 先进先出算法：FIFO,先调入内存的页先被置换淘汰，会产生抖动现象，即分配的页数越多，缺页率可能越多（即效率越低）
  经常使用的数据就会出去又进来，出去又进来的现象，这就是抖动
• 最近最少使用：LRU,在最近的过去，进程执行过程中，过去最少使用的页面被置换淘汰，根据局部性原理，这种方式效率高，且不会产生抖动现像。

练习题

【2021年】某进程有4个页面，页号为0~3，页面变换表及状态位、访问位和修改位的含义如下图所示，若系统给该进程分配了3个存储块，当访问前页面1不在内存时，淘汰表中页号为()的页面代价最小。

A.0
B.1
C.2
D.3

答案：D
页帧号：物理地址

快表

快表是一块小容量的相联存储器，由快速存储器组成，按内容访问，速度快，并且可以从硬件上保证按内容并行查找，一般用来存放当前访问最频繁的少数活动页面的页号（可以看成是页表的频繁访问数据的副本)。

快表和慢表都是页表，快表是页表的优化方式
快表是将页表存于Cache中；慢表是将页表存于内存上。因此慢表需要访问两次内存才能取出数据，而快表是访问一次Cache和一次内存，因比更快。