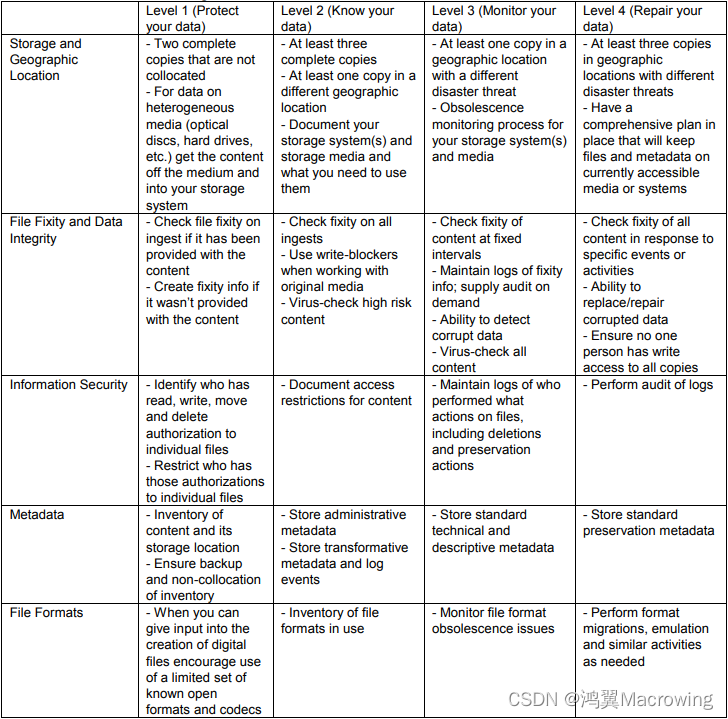
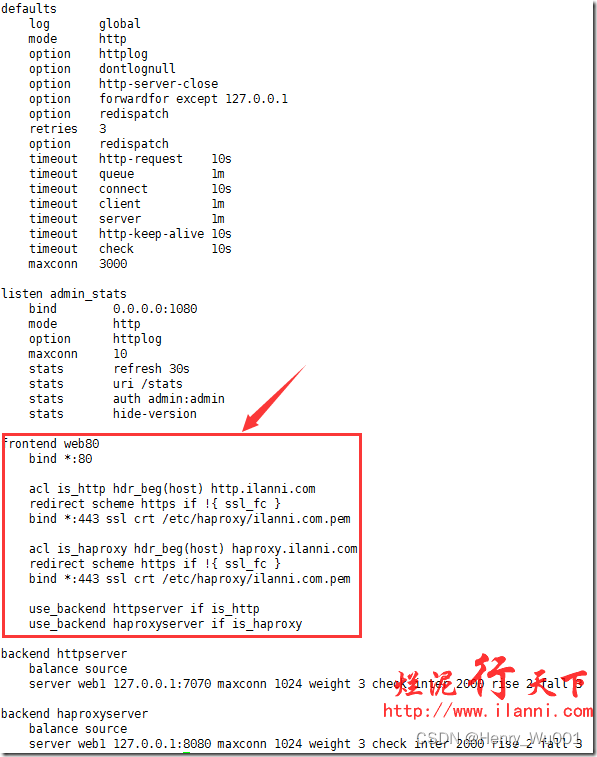
各位CSDN的uu们你们好呀，今天，小雅兰的内容是隐函数求导和参数方程求导，下面，就让我们进入求导数的世界吧
一、隐函数的导数
二、隐函数求导
三、由参数方程确定的函数的导数
四、相关变化率
一、隐函数的导数
要想知道隐函数的导数是什么，那么首先我们肯定要知道隐函数是什么呀
既然要知道隐函数是什么，我们还得知道一个概念，那就是函数。函数就是指：在某一变化过程中，两个变量x、y，对于某一范围内的x的每一个值，y都有确定的值和它对应，y就是x的函数。这种关系一般用y=f(x)即显函数来表示。
隐函数是由隐式方程所隐含定义的函数。设F（x,y）是某个定义域上的函数，如果存在定义域上的子集D，使得对每个x属于D，存在相应的y满足F(x,y)=0，则称方程确定了一个隐函数。记为y=y(x)。 显函数是用y=f(x)来表示的函数，显函数是相对于隐函数来说的。
下面来看几点注意事项
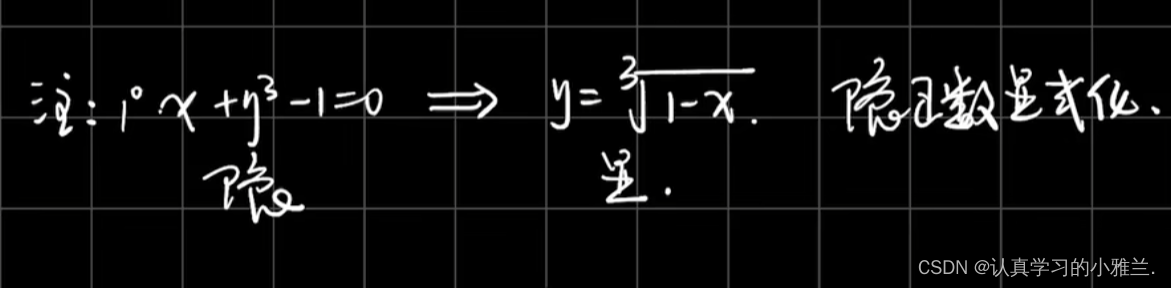
我们通常把隐函数显式化求导，是因为此隐函数的形式非常简单，而对于上面这个隐函数，显式化非常困难，所以肯定不能用这种方法来求导。
二、隐函数求导
注意事项
哎呀，死去的圆锥曲线开始攻击人了！！！其实，这道题目表面上看上去是一个圆锥曲线问题，实际上还是要我们求导。因为求一个点的切线方程，肯定是要求斜率的，对于此题，就是求x=2时的导数值。 
三、由参数方程确定的函数的导数
参数方程，为数学术语，其和函数很相似：它们都是由一些在指定的集的数，称为参数或自变量，以决定因变量的结果。例如在运动学，参数通常是“时间”，而方程的结果是速度、位置等。
一般地，在平面直角坐标系中，如果曲线上任意一点的坐标x、y都是某个变数t的函数：
并且对于t的每一个允许的取值，由方程组确定的点(x, y)都在这条曲线上，那么这个方程就叫做曲线的参数方程，联系变数x、y的变数t叫做参变数，简称参数。相对而言，直接给出点坐标间关系的方程即称为普通方程。
例子
曲线的极坐标参数方程ρ=f(t),θ=g(t)。
圆的参数方程 x=a+r cosθ y=b+r sinθ（θ∈ [0，2π) ） (a,b) 为圆心坐标，r 为圆半径，θ 为参数，(x,y) 为经过点的坐标
椭圆
椭圆的参数方程 x=a cosθ y=b sinθ（θ∈[0，2π）） a为长半轴长 b为短半轴长 θ为参数
双曲线的参数方程 x=a secθ （正割） y=b tanθ a为实半轴长 b为虚半轴长 θ为参数
抛物线的参数方程 x=2pt^2 y=2pt p表示焦点到准线的距离 t为参数
直线的参数方程 x=x'+tcosa y=y'+tsina,x',y'和a表示直线经过（x',y'），且倾斜角为a,t为参数
或者x=x'+ut， y=y'+vt (t∈R)x',y'直线经过定点（x',y'),u，v表示直线的方向向量d=(u,v)
圆的渐开线x=r(cosφ+φsinφ） y=r(sinφ-φcosφ）（φ∈[0,2π）） r为基圆的半径 φ为参数
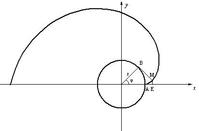
圆的渐开线
平摆线参数方程 x=r（θ-sinθ） y=r（1-cosθ）r为圆的半径，θ是圆的半径所经过的角度（滚动角），当θ由0变到2π时，动点就画出了摆线的一支，称为一拱。
平摆线
下面，我们来证明一下此定理
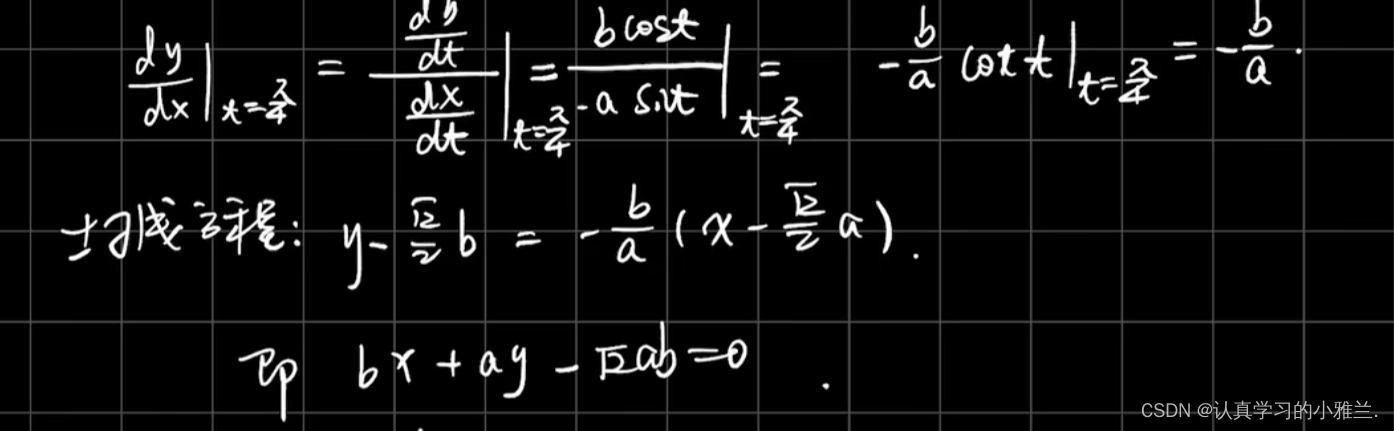
快看呐，死去的物理开始攻击人了！！！
特殊时刻
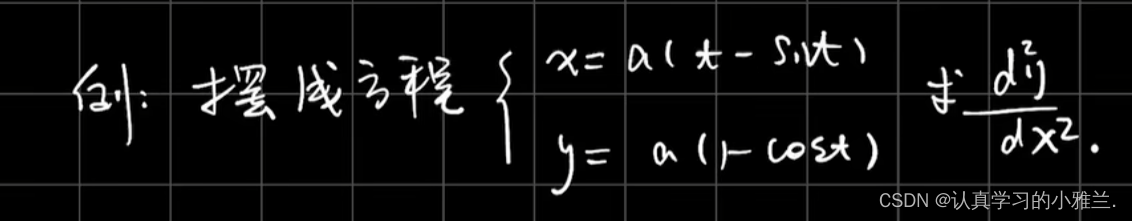
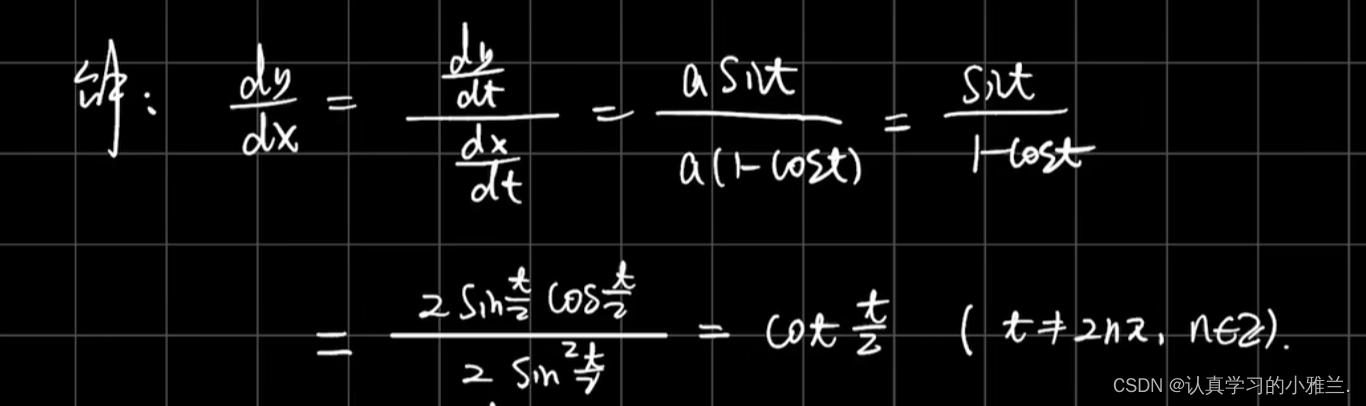
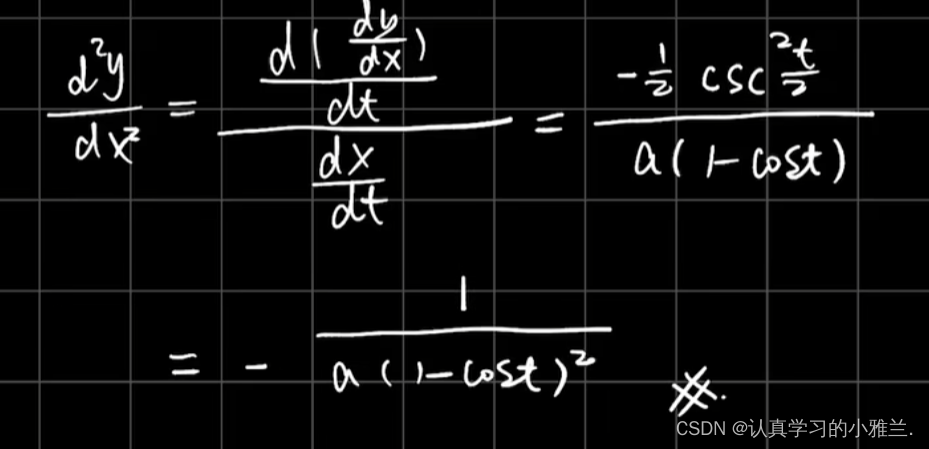
四、相关变化率 
这个定理理解起来比较抽象，下面还是用例题来说明
好啦，小雅兰今天的内容就到这里了，从此篇博客中，我们只需要知道隐函数是如何求导的和参数方程是如何求导的就可以了，相关变化率问题只需要了解一下。就快考试了，小雅兰持续输入高等数学中......
