一、问题

二、数位DP

这道题是在一个区间内挑选满足某个条件的数，这是一个非常典型的数位DP的特点。

这道题是一道数位DP的题目，其实数位DP更像我们在高中阶段学过的排列组合问题中的分类讨论。

数位DP顾名思义就是按照数字的每一位去讨论。

那么数位DP做题思路分为两步：按位枚举，分类讨论

我们把区间的上限X写出来：

那么怎么分类讨论呢？

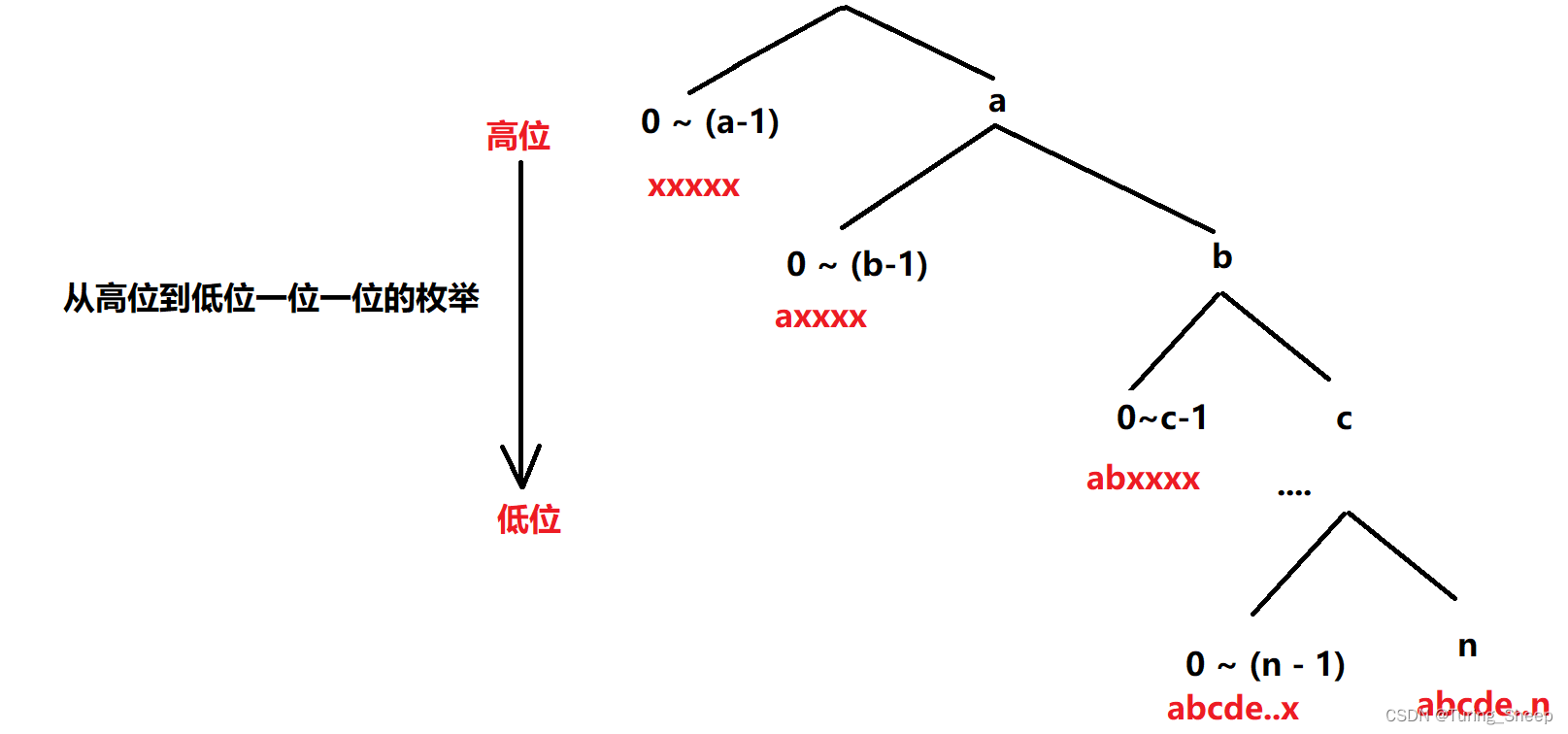
从上到下是从高位到低位枚举的，对于每一位我们的分类依据是：(0 ~ a - 1)和a，那么为什么这么分呢？

一般数位DP都是让我们挑选满足某个条件的数，我们不仅需要考虑某个数是否满足条件，还需要考虑某个数是否小于上限值。

那么我们在分类讨论以后，就发现我们分出的第一类情况中：0 ~ a-1，由于高位都小于了a，那么这个数肯定比上限X小，也就是说此时我们只需要考虑是否满足题目中的某个条件。

我们对每一位都做这样的操作，只不过越往下分，每个数字固定的前缀就越长，最后我们会发现所有二叉树的右儿子恰好组成了我们上限值。

那么有人可能会想，题目中问的有可能是个区间，难道我们不需要考虑这个数必须大于等于下限吗？

这里可以使用一个思路，假设$f[n]$是满足所有小于等于上限值的数的数量，我们只需要再减去小于下限m的数目，即$f[m-1]$的值，就是区间$[n,m]$内符合题目条件的数目。

三、思路分析

我们这道题也是从高位到低位枚举，但是和刚才的分类条件有一定的区别，刚才的图中左支是0到a-1，但是这道题要求不下降，所以假设a位前面一位是x的话，那么a所对位的左支范围应该是x到a-1。

我们拿出其中的一位为例子：

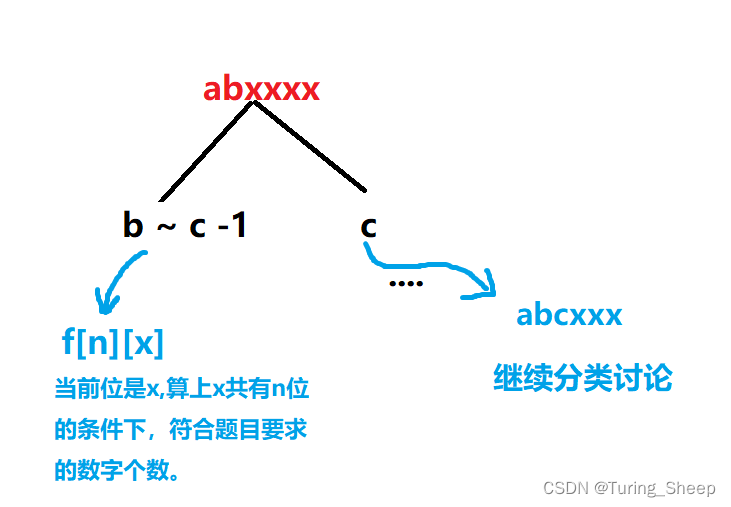
那么我们现在考虑一下左支的dp怎么写。

这个DP比较简单，就不详细讲了，上面这个图写的比较清楚了。

这里直接上代码。

四、代码

#include<bits/stdc++.h>
using namespace std;
const int N = 30;
int n, m;
int f[N][N];
void init()
{
	for(int i = 0; i <= 9; i ++ )f[1][i] = 1;
	for(int i = 2; i < N; i ++ )
		for(int j = 0; j <= 9; j ++ )
			for(int k = j; k <= 9; k ++ )
				f[i][j] += f[i - 1][k];
}
int dp(int x)
{
  if(!x)return 1;
	int res = 0;
	int last = 0;
	vector<int> v;
	while(x)
	{
		v.push_back(x % 10);
		x /= 10;
	}
	for(int i = v.size() - 1; i >= 0; i -- )
	{
		int a = v[i];
		
		//左支
		for(int j = last; j < a; j ++ )
		{
			res += f[i + 1][j];
		}
		if(last > a) break;
		//右支
		last = a;
		if(!i)res ++;
	}
	return res;
}

int main()
{
	init();
    while(scanf("%d%d",&n, &m) != EOF)
        cout << dp(m) - dp(n - 1) << endl;
    return 0;
}