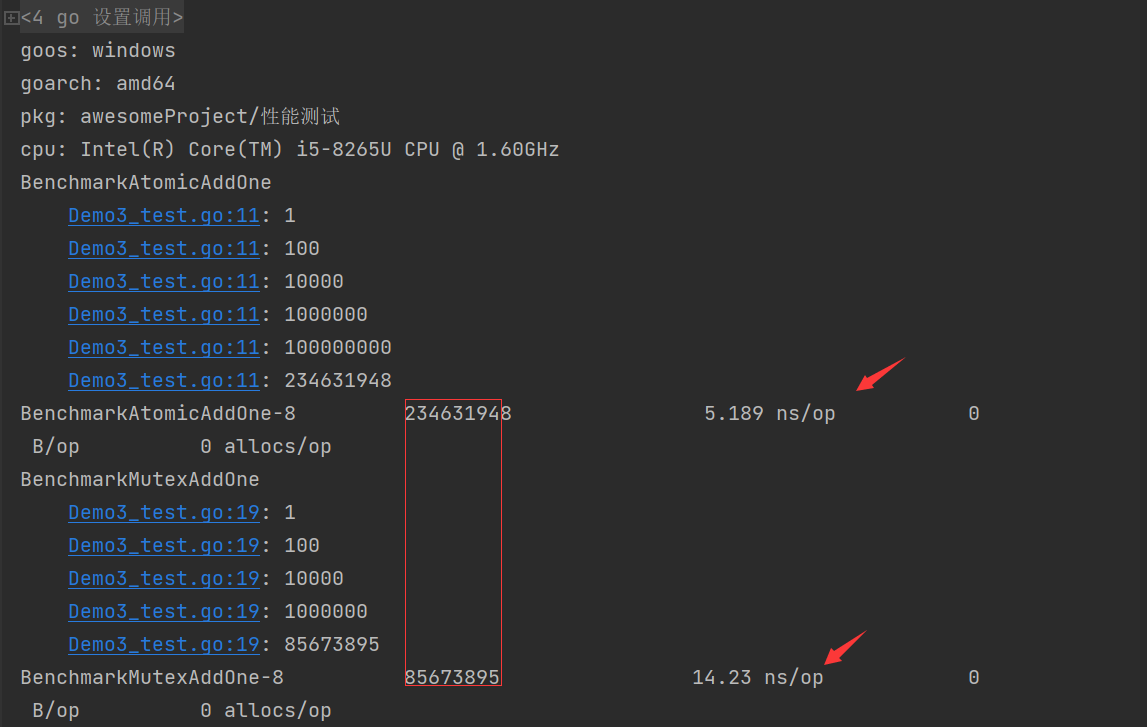
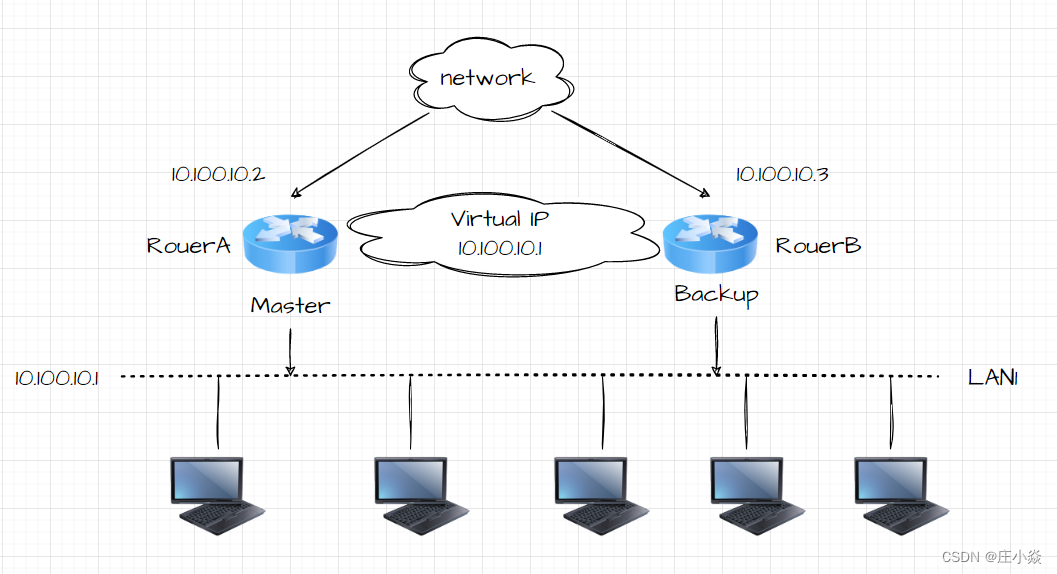
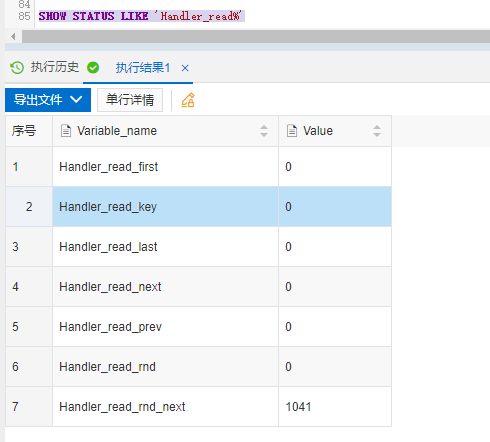
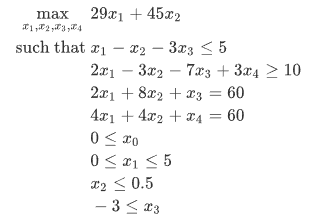PID控制模型
负反馈控制模型,到处都挺常见的,我记得高中的时候生物上就有一堆,什么体液调节之类的。PID控制也算是经典控制了,大家讲的都是经验之谈,这里我从误差曲线调节的角度来讲(误差曲线调节一般都是神经网络上谈的)。
PID模型
常分为位置式PID和增量式PID:
位置式: o u t = K p ∗ e k + K i ∗ ∑ e k + K d ∗ [ e k − e k − 1 ] out = K_p*e_k+K_i*∑e_k+K_d*[e_k-e_{k-1}] out=Kp∗ek+Ki∗∑ek+Kd∗[ek−ek−1]
简记 o u t = K p ∗ e k + K i ∗ ∑ e k + K d ∗ e k ′ out = K_p*e_k+K_i*∑e_k+K_d*e_k' out=Kp∗ek+Ki∗∑ek+Kd∗ek′
增量式: o u t + = K p ∗ [ e k − e k − 1 ] + K i ∗ e k + K d ∗ [ e k − 2 e k − 1 + e k − 2 ] out += K_p*[e_k-e_{k-1}] + K_i*e_k+K_d*[e_k-2e_{k-1}+e_{k-2}] out+=Kp∗[ek−ek−1]+Ki∗ek+Kd∗[ek−2ek−1+ek−2]
简记 o u t + = K p ∗ e k ′ + K i ∗ e k + K d ∗ e k ′ ′ out += K_p*e_k' + K_i*e_k+K_d*e_k'' out+=Kp∗ek′+Ki∗ek+Kd∗ek′′
待控制系统
我这里将待控制系统的模型分为两类:孤立系统和耗散系统
下图中,为一个桶,红色的是目标高度,假设橙色液体是水
1、孤立系统:
这种系统的特性就是你加一滴水,他就有一滴水留存
2、耗散系统
这种系统的特性就是你加一滴水,这滴水会自己从底部漏完然后消失
模型输出使得误差曲线降为0
控制理论中,我们常用的说法是这样:将桶的水位控制到目标高度(红线)。
负反馈调节
如上图中,水位低于目标高度(负值)时,我们需要往桶里加水(正值),才能使得水位更接近于目标,这便是负反馈调节,我们的操作输出和系统实际状态是相反,两者此消彼长维持系统平衡。
误差控制
我们若假设实际误差为:
E
r
r
o
=
O
b
s
e
r
v
−
T
a
r
g
e
t
Err_o = Observ - Target
Erro=Observ−Target,即实际误差 = 实际观测值 - 目标值 。
这样我们就不用关心正反馈还是负反馈了:
负反馈: o u t = − E r r o out = -Err_o out=−Erro
正反馈: o u t = E r r o out = Err_o out=Erro需要注意的是,这里的误差和pid算法中的误差刚好是相反的
至此,控制算法模型摆脱实际问题,成为独立的数学模型:控制模型的输出是误差的函数
误差曲线
当我们人为操纵待控制系统时,它的误差就会随着变化,我们的目标就只有一个:控制模型输出使得误差为0。
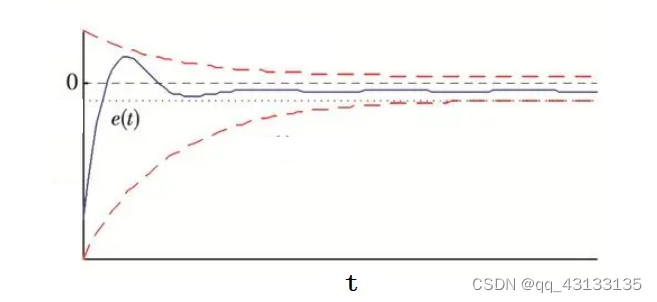 对于之前所述的孤立系统而言,我们只要假设单次加水量
W
a
d
d
W_{add}
Wadd:
对于之前所述的孤立系统而言,我们只要假设单次加水量
W
a
d
d
W_{add}
Wadd:
W a d d = − E r r o W_{add} = - Err_o Wadd=−Erro
水没达到标高,就多加点水,水高于标高,就倒出点水,慢慢的水位就可以到达标高了。
当然,还有一个细节问题,就是单位,量级问题,比如说我加水用的是单位是 m 3 m^3 m3,对于一个桶和一根管,横截面积不同,加相同水的影响就不同,我们可以增加一个系数k,通过调节系数使得实际影响相同:
W a d d = − k ∗ E r r o W_{add} = - k*Err_o Wadd=−k∗Erro这样做必然是有好处的,我们只需研究一个标准系统,其余的系统我们可以通过调节k参数将其转化为标准系统的等效系统,这样就能将之前研究成果应用在新的系统上了。
对于耗散系统而言,我们若假设单次加水量 W a d d W_{add} Wadd和之前一样,便会出现一个问题:
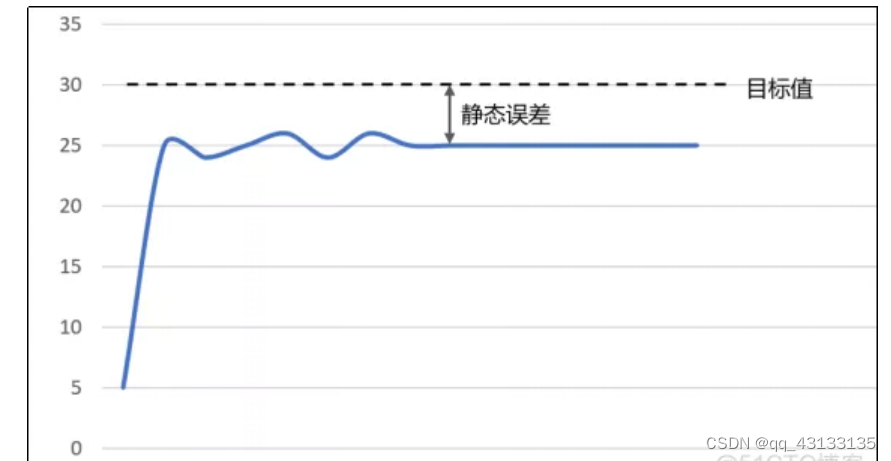
由于一直在漏水,达到平衡后将有:漏水量=加水量,由于漏水量不为0,所以必然有一个恒定误差,使得 W a d d W_{add} Wadd不为0,也就是我们常说的净差
我们需要做的就是在输出中加上一个输出常数 C C C,其值与漏水量相等,通过弥补常数抵消漏水影响,就可以使该系统转化为之前的孤立系统,剩下的和之前一样了
W a d d = − ( k ∗ E r r o + C ) W_{add} = - (k*Err_o + C) Wadd=−(k∗Erro+C)
这个常数 C C C,我们是可以通过累计静态误差得到的,直到静态误差为0,累计值便不再增加:
C = k 2 ∗ ∑ e ( t ) C =k_2*∑e(t) C=k2∗∑e(t)
k 2 k_2 k2参数可以根据系统响应进行调整,若是系统响应的较慢,则参数应取较小值,若取太大了,使得 C C C常数>漏水量,输出就会产生一定的震荡区间,使得 C C C常数有时>漏水量,有时<漏水量。
当然,通常会对 C 项 C项 C项进行积分限幅,比如漏水量最多不超过50,结果由于你的参数取太大了,导致算得C参数都为1000了,这样还会影响后续系统调整,导致调整滞后,引发系统进行发散式震荡。
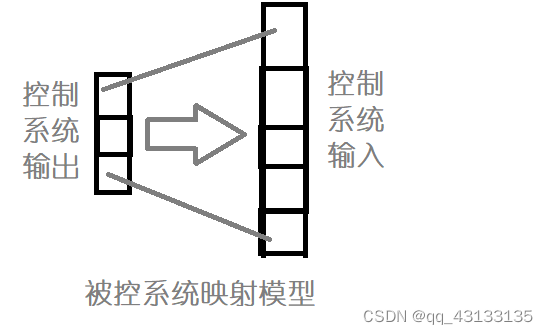
输入与输出的区间映射
对于控制系统而言,一般采用离散输出,这里便存在一个分辨率的问题:
加上输出范围是[-1,0,1]三个值,而输入范围是[-2,-1,0,1,2],系统必然是要震荡的
假设输出恒为1时,输入为2;输出为-1时,输入为-2。那么我若想让输入为-1,则输出必然是在0和1之间震荡的,按照一定概率比例的0和1组合才能实现。之前在静态误差累计部分说到 k 2 k_2 k2参数若取的偏大,就会造成系统震荡,便是这个原因, k 2 k_2 k2参数太大会使得输出分辨率降低。
对于一个要稳定控制的系统,其分辨率至少要保证控制系统输出分辨率 ≥ 控制系统输入分辨率
输出控制的频率
如果控制输出的频率太快了,比如说我往桶里倒水,结果我的水才刚倒出还飘在空中,我又进行下一次控制系统运算,采集得到的还是原来是量,这个就会产生滞后性,容易引发震荡(但可以通过降低控制系数来规避),所以控制频率最好根据被控系统的响应时间来估计一下。
如果控制太慢了,就会感觉到系统响应延迟,我设置目标值要好一会,才能到达状态。这就是控制模型和系统响应时间不匹配,产生的控制滞后了。